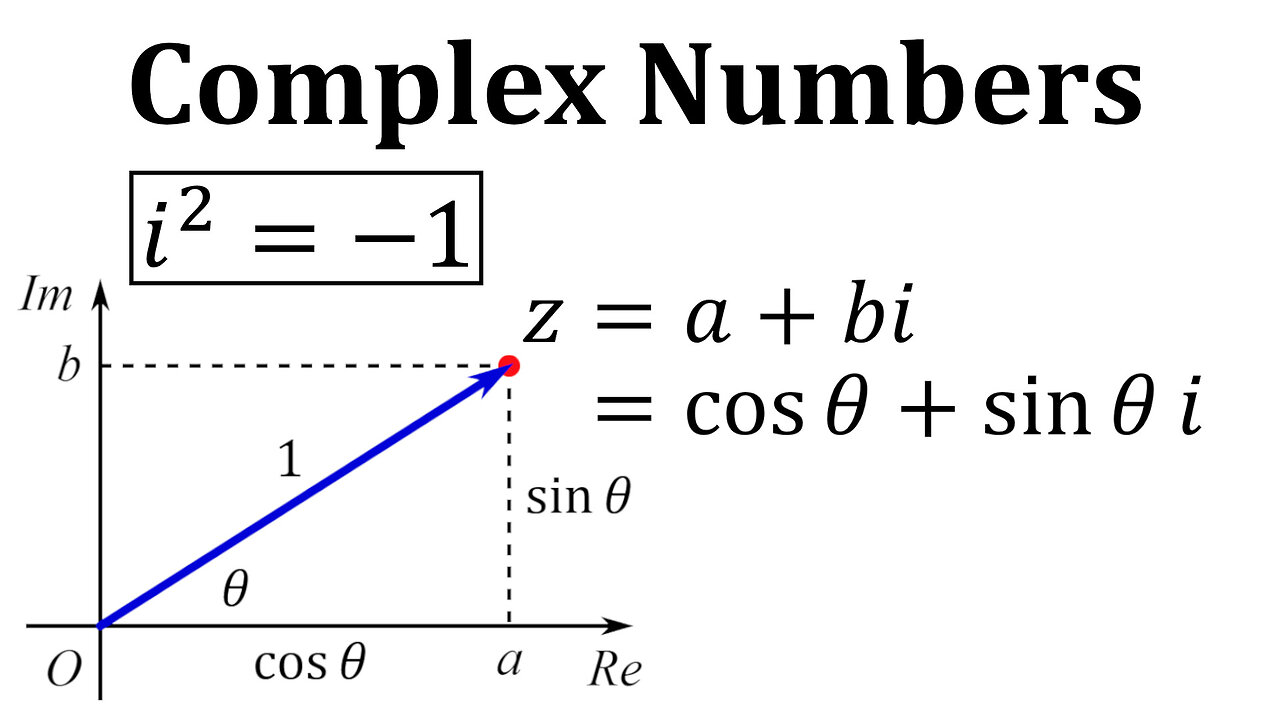E^z Complex Number . For any complex number z = x + iy, with x and y real, the exponential ez, is defined by. (r is the absolute value of the complex number, the same as we had before in the polar form; The exponential form of a complex number is: In particular 2, eiy = cosy +. Consider the complex exponential function $f : You can add, multiply and divide complex numbers. Ex + iy = excosy + iexsiny. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. + w = (a + bi). The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\) such that. \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. To add (subtract) z = a + bi and w = c + di. For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x.
from rumble.com
For any complex number z = x + iy, with x and y real, the exponential ez, is defined by. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. Consider the complex exponential function $f : Ex + iy = excosy + iexsiny. \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. To add (subtract) z = a + bi and w = c + di. The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\) such that. The exponential form of a complex number is: You can add, multiply and divide complex numbers.
Complex Numbers Definition and Vector Form
E^z Complex Number In particular 2, eiy = cosy +. The exponential form of a complex number is: For any complex number z = x + iy, with x and y real, the exponential ez, is defined by. (r is the absolute value of the complex number, the same as we had before in the polar form; For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. To add (subtract) z = a + bi and w = c + di. In particular 2, eiy = cosy +. Consider the complex exponential function $f : You can add, multiply and divide complex numbers. \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\) such that. Ex + iy = excosy + iexsiny. + w = (a + bi).
From www.askpython.com
Python Complex Numbers AskPython E^z Complex Number For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. Consider the complex exponential function $f : The exponential form of a complex number is: For any complex number z = x + iy, with x and. E^z Complex Number.
From mathsathome.com
How to Find the Modulus and Argument of a Complex Number E^z Complex Number The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\) such that. The exponential form of a complex number is: In particular 2, eiy = cosy +. \mathbb{c}\to \mathbb{c}$ given. E^z Complex Number.
From www.alamy.com
Parts of complex number in mathematics. imaginary part and real part E^z Complex Number \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. For any complex number z = x + iy, with x and y real, the exponential ez, is defined by. \mathbb{c}\to \mathbb{c}$ given by $f ( z. E^z Complex Number.
From www.youtube.com
How to Find Conjugate of Complex Number Complex Numbers Math Class 9th E^z Complex Number \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. + w = (a + bi). Consider the complex exponential function $f : Ex + iy = excosy + iexsiny. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. (r is the absolute value of the complex number, the same as we had before in the polar form; The. E^z Complex Number.
From quickmath.com
Basics of complex number StepbyStep Math Problem Solver E^z Complex Number You can add, multiply and divide complex numbers. To add (subtract) z = a + bi and w = c + di. + w = (a + bi). \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. Ex + iy = excosy + iexsiny. For \(z = x + iy\) the complex exponential function is defined as \[e^z =. E^z Complex Number.
From mathsathome.com
How to Find the Modulus and Argument of a Complex Number E^z Complex Number To add (subtract) z = a + bi and w = c + di. Ex + iy = excosy + iexsiny. Consider the complex exponential function $f : You can add, multiply and divide complex numbers. For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. The. E^z Complex Number.
From www.ck12.org
Defining Complex Numbers ( Read ) Trigonometry CK12 Foundation E^z Complex Number You can add, multiply and divide complex numbers. For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. + w = (a + bi). In particular 2, eiy = cosy +. Consider the complex exponential function $f : \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j. E^z Complex Number.
From mathsathome.com
How to Find the Modulus and Argument of a Complex Number E^z Complex Number \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. Consider the complex exponential function $f : The exponential form of a complex number is: (r is the absolute value of the complex number, the same as we had before in the polar form; The absolute value of a complex number \(z = x + iy\) is given by \(\left. E^z Complex Number.
From owlcation.com
Math How to Use Complex Numbers and the Complex Plane Owlcation E^z Complex Number \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. The exponential form of a complex number is: + w = (a + bi). For any complex number z = x + iy, with x and y real, the exponential ez, is defined by. The absolute value of a complex number \(z = x + iy\) is given by \(\left. E^z Complex Number.
From mathsathome.com
How to Find the Modulus and Argument of a Complex Number E^z Complex Number (r is the absolute value of the complex number, the same as we had before in the polar form; To add (subtract) z = a + bi and w = c + di. The exponential form of a complex number is: Consider the complex exponential function $f : + w = (a + bi). Ex + iy = excosy +. E^z Complex Number.
From www.youtube.com
Complex Numbers Exponential Form or Euler's Form ExamSolutions E^z Complex Number The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\) such that. Ex + iy = excosy + iexsiny. For any complex number z = x + iy, with x. E^z Complex Number.
From www.youtube.com
Complex numbers Solving Equations (with example) YouTube E^z Complex Number You can add, multiply and divide complex numbers. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\) such that.. E^z Complex Number.
From mathsathome.com
How to Find the Modulus and Argument of a Complex Number E^z Complex Number \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. In particular 2, eiy = cosy +. Ex + iy = excosy + iexsiny. For any complex. E^z Complex Number.
From mathsathome.com
How to Find the Modulus and Argument of a Complex Number E^z Complex Number \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. To add (subtract) z = a + bi and w = c + di. The exponential form of a complex number is: You can add, multiply and divide complex numbers. For any complex number z = x + iy, with x and y real, the exponential ez, is defined by.. E^z Complex Number.
From mavink.com
Complex Number Venn Diagram E^z Complex Number \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. Ex + iy = excosy + iexsiny. The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | =. E^z Complex Number.
From www.slideserve.com
PPT Trigonometric Form of a Complex Number PowerPoint Presentation E^z Complex Number Ex + iy = excosy + iexsiny. The exponential form of a complex number is: You can add, multiply and divide complex numbers. \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. (r is the absolute value of the complex number, the same as we had before in the polar form; To add (subtract) z = a + bi. E^z Complex Number.
From www.slideserve.com
PPT Complex number PowerPoint Presentation, free download ID4983846 E^z Complex Number The exponential form of a complex number is: Consider the complex exponential function $f : For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. In particular 2, eiy = cosy +. For any complex number z = x + iy, with x and y real, the. E^z Complex Number.
From www.expii.com
Exponential Form of a Complex Number Expii E^z Complex Number (r is the absolute value of the complex number, the same as we had before in the polar form; \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. To add (subtract) z = a + bi and w = c + di. Ex + iy = excosy + iexsiny.. E^z Complex Number.
From mathsathome.com
How to Use De Moivre’s Theorem to Find Powers of Complex Numbers E^z Complex Number The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\) such that. You can add, multiply and divide complex numbers. For \(z = x + iy\) the complex exponential function. E^z Complex Number.
From mathsathome.com
How to Find the Modulus and Argument of a Complex Number E^z Complex Number For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. + w = (a + bi). Ex + iy = excosy + iexsiny. Consider the complex exponential function $f : For any complex number z = x + iy, with x and y real, the exponential ez,. E^z Complex Number.
From ncvm4.books.nba.co.za
Complex Numbers Working with complex numbers National Curriculum E^z Complex Number For any complex number z = x + iy, with x and y real, the exponential ez, is defined by. The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\). E^z Complex Number.
From mathsathome.com
How to Find the Modulus and Argument of a Complex Number E^z Complex Number The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\) such that. Consider the complex exponential function $f : In particular 2, eiy = cosy +. To add (subtract) z. E^z Complex Number.
From www.youtube.com
Complex numbers with examples Introduction YouTube E^z Complex Number For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. In particular 2, eiy = cosy +. The exponential form of a complex number is: \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. Consider the. E^z Complex Number.
From studylib.es
The Modulus/Argument form of a complex number E^z Complex Number To add (subtract) z = a + bi and w = c + di. (r is the absolute value of the complex number, the same as we had before in the polar form; \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. + w = (a + bi). \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. Ex. E^z Complex Number.
From www.slideserve.com
PPT Trigonometric Form of a Complex Number PowerPoint Presentation E^z Complex Number Consider the complex exponential function $f : \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. In particular 2, eiy = cosy +. For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. For any complex number z = x + iy, with x and y. E^z Complex Number.
From rumble.com
Complex Numbers Definition and Vector Form E^z Complex Number \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. Consider the complex exponential function $f : For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. (r is the absolute value of the complex number, the same as we had before in the polar form; The. E^z Complex Number.
From www.numerade.com
Find the magnitude and angle of these complex numbers e) z = (1+j)(1j E^z Complex Number You can add, multiply and divide complex numbers. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. Ex + iy = excosy + iexsiny. In particular 2, eiy = cosy +. \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. For any complex number z = x + iy, with x and y real, the exponential ez, is. E^z Complex Number.
From www.pinterest.com
Complex numbers Complex numbers, Studying math, Math methods E^z Complex Number \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. For any complex number z = x + iy, with x and y real, the exponential ez, is defined by. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. (r is the absolute value of the complex number, the same as we had before in the polar form; For. E^z Complex Number.
From www.aakash.ac.in
Complex Numbers Definition, Properties & Geometrical Representation AESL E^z Complex Number (r is the absolute value of the complex number, the same as we had before in the polar form; To add (subtract) z = a + bi and w = c + di. Consider the complex exponential function $f : For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x. E^z Complex Number.
From www.slideserve.com
PPT Complex Numbers PowerPoint Presentation, free download ID6511654 E^z Complex Number \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. Consider the complex exponential function $f : (r is the absolute value of the complex number, the same as we had before in the polar form; + w = (a + bi). You can add, multiply and divide complex numbers. The absolute value of a complex number \(z = x. E^z Complex Number.
From www.youtube.com
The Complex Exponential Function f(z) = e^z is Entire Proof YouTube E^z Complex Number The exponential form of a complex number is: For \(z = x + iy\) the complex exponential function is defined as \[e^z = e^{x + iy} = e^x e^{iy} = e^x. \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. For any complex number z = x + iy,. E^z Complex Number.
From www.houseofmath.com
What Is Euler’s Formula for Complex Numbers? House of Math E^z Complex Number \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex number \(z = x + iy\) is given by \(\theta\) such that. (r is the absolute value of the complex. E^z Complex Number.
From chalkdustmagazine.com
Complex numbers and algebra Chalkdust E^z Complex Number You can add, multiply and divide complex numbers. To add (subtract) z = a + bi and w = c + di. The exponential form of a complex number is: The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or phase) of a complex. E^z Complex Number.
From www.alamy.com
Parts of complex number in mathematics. imaginary part and real part E^z Complex Number \displaystyle {r} {e}^ { {\ {j}\ \theta}} re j θ. \mathbb{c}\to \mathbb{c}$ given by $f ( z ) = e^z$. To add (subtract) z = a + bi and w = c + di. The absolute value of a complex number \(z = x + iy\) is given by \(\left |z \right | = \sqrt{x^2 + y^2}.\) the argument (or. E^z Complex Number.
From mr-mathematics.com
Exponential Form of Complex Numbers E^z Complex Number To add (subtract) z = a + bi and w = c + di. Ex + iy = excosy + iexsiny. In particular 2, eiy = cosy +. For any complex number z = x + iy, with x and y real, the exponential ez, is defined by. + w = (a + bi). For \(z = x + iy\). E^z Complex Number.