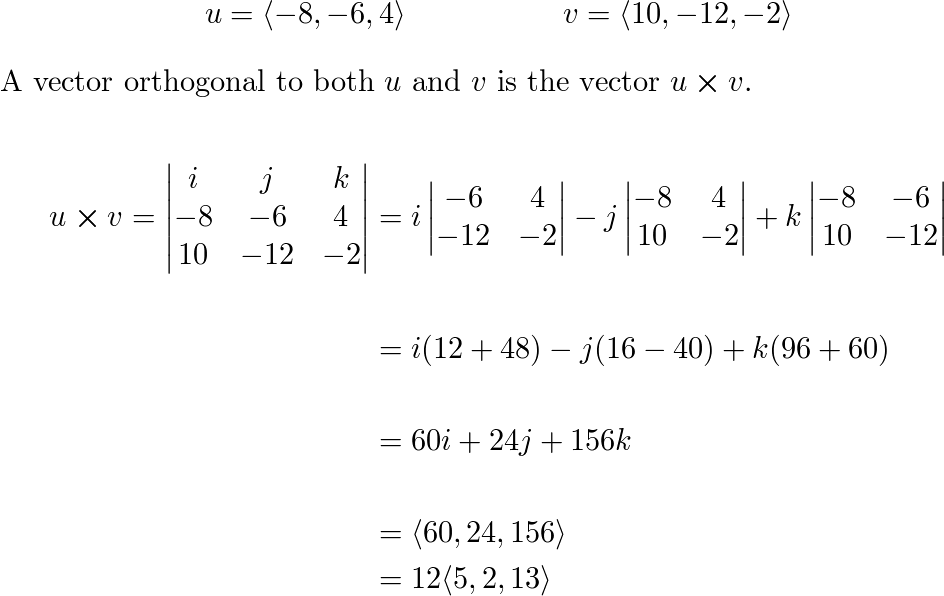Orthogonal Matrix Unit Vector . An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. The precise definition is as follows. Orthogonal matrices are those preserving the dot product. Understand the relationship between the dot product, length, and distance. A set is orthonormal if it is orthogonal and each vector is a unit vector. N (r) is orthogonal if av · aw = v · w for all vectors v. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Understand the relationship between the dot. A matrix a ∈ gl. An orthonormal basis is a basis whose vectors are. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1.
from quizlet.com
Understand the relationship between the dot. An orthonormal basis is a basis whose vectors are. An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. A matrix a ∈ gl. The precise definition is as follows. Understand the relationship between the dot product, length, and distance. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. N (r) is orthogonal if av · aw = v · w for all vectors v. A set is orthonormal if it is orthogonal and each vector is a unit vector.
Find a unit vector that is orthogonal to both u and v. u = Quizlet
Orthogonal Matrix Unit Vector Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. A matrix a ∈ gl. An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. A set is orthonormal if it is orthogonal and each vector is a unit vector. Understand the relationship between the dot. An orthonormal basis is a basis whose vectors are. Understand the relationship between the dot product, length, and distance. Orthogonal matrices are those preserving the dot product. The precise definition is as follows. N (r) is orthogonal if av · aw = v · w for all vectors v.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Orthogonal Matrix Unit Vector A matrix a ∈ gl. The precise definition is as follows. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. Orthogonal matrices are those preserving. Orthogonal Matrix Unit Vector.
From www.bartleby.com
Answered a) Given the rotation matrix 1 R=0 1 0… bartleby Orthogonal Matrix Unit Vector Understand the relationship between the dot product, length, and distance. A set is orthonormal if it is orthogonal and each vector is a unit vector. Orthogonal matrices are those preserving the dot product. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is. Orthogonal Matrix Unit Vector.
From teamlab.github.io
Basic Linear Algebra Orthogonal Matrix Unit Vector Understand the relationship between the dot. The precise definition is as follows. N (r) is orthogonal if av · aw = v · w for all vectors v. Understand the relationship between the dot product, length, and distance. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal. Orthogonal Matrix Unit Vector.
From www.youtube.com
How to find many vectors orthogonal to given in vector three space Orthogonal Matrix Unit Vector N (r) is orthogonal if av · aw = v · w for all vectors v. The precise definition is as follows. A set is orthonormal if it is orthogonal and each vector is a unit vector. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. Understand the relationship between the dot. Orthogonal matrix is a. Orthogonal Matrix Unit Vector.
From www.slideserve.com
PPT Row and column matrices are sometimes called row vectors and Orthogonal Matrix Unit Vector When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Orthogonal matrices are those preserving the dot product. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to. Orthogonal Matrix Unit Vector.
From www.researchgate.net
Threedimensional representation of the orthogonal vector space basis Orthogonal Matrix Unit Vector Orthogonal matrices are those preserving the dot product. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. The precise definition is as follows. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and. Orthogonal Matrix Unit Vector.
From www.youtube.com
Orthogonal Vectors Example 1 YouTube Orthogonal Matrix Unit Vector A matrix a ∈ gl. An orthonormal basis is a basis whose vectors are. N (r) is orthogonal if av · aw = v · w for all vectors v. Orthogonal matrices are those preserving the dot product. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal. Orthogonal Matrix Unit Vector.
From slidetodoc.com
Orthogonal Vector Hungyi Lee Orthogonal Set A set Orthogonal Matrix Unit Vector A matrix a ∈ gl. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. An orthonormal basis is a basis whose vectors are. The precise definition is as follows. N (r) is orthogonal if av · aw = v · w for all vectors v. An. Orthogonal Matrix Unit Vector.
From www.numerade.com
SOLVED find two unit vector orthogonal to both (ij) and (i+j) Orthogonal Matrix Unit Vector When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. The precise definition is as follows. An orthonormal basis is a basis whose vectors are. A matrix a ∈ gl. Orthogonal matrices are those preserving the dot product. N (r) is orthogonal if av · aw =. Orthogonal Matrix Unit Vector.
From quizlet.com
Find a unit vector that is orthogonal to both u and v. u = Quizlet Orthogonal Matrix Unit Vector Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. Understand the relationship between the dot product, length, and distance. N (r) is orthogonal if av. Orthogonal Matrix Unit Vector.
From slidetodoc.com
Orthogonal Vector Hungyi Lee Orthogonal Set A set Orthogonal Matrix Unit Vector N (r) is orthogonal if av · aw = v · w for all vectors v. Understand the relationship between the dot product, length, and distance. A set is orthonormal if it is orthogonal and each vector is a unit vector. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is. Orthogonal Matrix Unit Vector.
From www.youtube.com
Orthogonal and Orthonormal Vectors Linear Algebra YouTube Orthogonal Matrix Unit Vector When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Understand the relationship between the dot product, length, and distance. Orthogonal matrices are those preserving the dot product. An orthonormal basis is a basis whose vectors are. An orthogonal matrix \(u\), from definition 4.11.7 , is one. Orthogonal Matrix Unit Vector.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint Orthogonal Matrix Unit Vector An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. A set is orthonormal if it is orthogonal and each vector is a unit vector. An orthonormal basis is a basis whose vectors are. Orthogonal matrices are those preserving the dot product. A. Orthogonal Matrix Unit Vector.
From www.youtube.com
Orthogonal projection of a vector onto a plane. YouTube Orthogonal Matrix Unit Vector Understand the relationship between the dot product, length, and distance. The precise definition is as follows. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. An orthonormal basis is a basis whose vectors are. A set is orthonormal if it is orthogonal and each vector is a unit vector. N (r) is orthogonal if av ·. Orthogonal Matrix Unit Vector.
From www.numerade.com
SOLVEDFind a unit vector u orthogonal to v=[1,3,4] and w=[2,6,5] Orthogonal Matrix Unit Vector Understand the relationship between the dot product, length, and distance. The precise definition is as follows. Orthogonal matrices are those preserving the dot product. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each. Orthogonal Matrix Unit Vector.
From www2.seas.gwu.edu
Linear Algebra Orthogonal Matrix Unit Vector When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A matrix a ∈ gl. Orthogonal matrices are those preserving the dot product. An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. An orthogonal matrix \(u\), from definition 4.11.7 , is one. Orthogonal Matrix Unit Vector.
From study.com
Orthogonal Vectors Overview, Formula & Examples Lesson Orthogonal Matrix Unit Vector A set is orthonormal if it is orthogonal and each vector is a unit vector. Understand the relationship between the dot product, length, and distance. Orthogonal matrices are those preserving the dot product. An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. When an \(n \times n\) matrix has all real entries and its transpose. Orthogonal Matrix Unit Vector.
From www.slideserve.com
PPT EE2030 (I) PowerPoint Presentation, free Orthogonal Matrix Unit Vector An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. Understand the relationship between the dot. The precise definition is as follows. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. Understand the relationship between the dot product, length, and distance. An orthonormal basis is a basis whose vectors are. When an. Orthogonal Matrix Unit Vector.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix How to prove Orthogonal Orthogonal Matrix Unit Vector Understand the relationship between the dot product, length, and distance. The precise definition is as follows. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1.. Orthogonal Matrix Unit Vector.
From www.youtube.com
unit vector, orthogonal vector Linear Algebra YouTube Orthogonal Matrix Unit Vector An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. The precise definition is as follows. N (r) is orthogonal if av · aw = v · w for all vectors v. Understand the relationship between the dot product, length, and distance. Understand. Orthogonal Matrix Unit Vector.
From technikermathe.de
Zerlegung von Vektoren Einfach gut erklärt 1a [BEISPIEL] Orthogonal Matrix Unit Vector Understand the relationship between the dot. An orthonormal basis is a basis whose vectors are. Orthogonal matrices are those preserving the dot product. A matrix a ∈ gl. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. N (r) is orthogonal if av · aw =. Orthogonal Matrix Unit Vector.
From www.slideserve.com
PPT Numerical Linear Algebra PowerPoint Presentation, free download Orthogonal Matrix Unit Vector Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. Orthogonal matrices are those preserving the dot product. An orthonormal basis is a basis whose vectors. Orthogonal Matrix Unit Vector.
From www.youtube.com
14 Unit Vectors Orthogonal Unit Vector Class 11 Physics Orthogonal Matrix Unit Vector A matrix a ∈ gl. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning. Orthogonal Matrix Unit Vector.
From www.slideshare.net
Orthogonal porjection in statistics Orthogonal Matrix Unit Vector Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row and column, and each row or column has a magnitude of 1. An orthonormal basis is a basis whose vectors are. Orthogonal matrices are those preserving the dot. Orthogonal Matrix Unit Vector.
From www.youtube.com
Orthogonal Vectors Using Pythagorean Theorem Example 1 YouTube Orthogonal Matrix Unit Vector An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. Understand the relationship between the dot product, length, and distance. A matrix a ∈ gl. N (r) is orthogonal if av · aw = v · w for all vectors v. The precise definition is as follows. Orthogonal matrix is a square matrix in which all rows. Orthogonal Matrix Unit Vector.
From youtube.com
1.3 Orthogonal Vectors YouTube Orthogonal Matrix Unit Vector When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A matrix a ∈ gl. Understand the relationship between the dot product, length, and distance. Understand the relationship between the dot. A set is orthonormal if it is orthogonal and each vector is a unit vector. Orthogonal. Orthogonal Matrix Unit Vector.
From www.youtube.com
Orthogonal and Orthonormal vectors and Matrices, Diagonal Matrix Orthogonal Matrix Unit Vector Orthogonal matrices are those preserving the dot product. A set is orthonormal if it is orthogonal and each vector is a unit vector. N (r) is orthogonal if av · aw = v · w for all vectors v. The precise definition is as follows. Understand the relationship between the dot. An orthogonal matrix \(u\), from definition 4.11.7 , is. Orthogonal Matrix Unit Vector.
From www.youtube.com
Vector Cross Product Orthogonal Unit Vectors YouTube Orthogonal Matrix Unit Vector When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. An orthogonal matrix is a matrix whose column vectors are orthonormal to each other. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. An orthonormal basis is a basis whose vectors are. Orthogonal. Orthogonal Matrix Unit Vector.
From mathsathome.com
How to Find a Vector Perpendicular to a Plane Orthogonal Matrix Unit Vector When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. An orthonormal basis is a basis whose vectors are. The precise definition is as follows. A set is orthonormal if it is orthogonal and each vector is a unit vector. N (r) is orthogonal if av ·. Orthogonal Matrix Unit Vector.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Orthogonal Matrix Unit Vector An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. A set is orthonormal if it is orthogonal and each vector is a unit vector. Understand the relationship between the dot product, length, and distance. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal. Orthogonal Matrix Unit Vector.
From slidetodoc.com
Orthogonal Vector Hungyi Lee Orthogonal Set A set Orthogonal Matrix Unit Vector When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Understand the relationship between the dot product, length, and distance. A matrix a ∈ gl. N (r) is orthogonal if av · aw = v · w for all vectors v. Understand the relationship between the dot.. Orthogonal Matrix Unit Vector.
From 911weknow.com
[Linear Algebra] 9. Properties of orthogonal matrices 911 WeKnow Orthogonal Matrix Unit Vector N (r) is orthogonal if av · aw = v · w for all vectors v. Understand the relationship between the dot product, length, and distance. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Understand the relationship between the dot. An orthonormal basis is a. Orthogonal Matrix Unit Vector.
From www.youtube.com
Orthogonal vectors YouTube Orthogonal Matrix Unit Vector N (r) is orthogonal if av · aw = v · w for all vectors v. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A matrix a ∈ gl. A set is orthonormal if it is orthogonal and each vector is a unit vector. Orthogonal. Orthogonal Matrix Unit Vector.
From www.geogebra.org
Vectors Unit Vector & Orthogonal GeoGebra Orthogonal Matrix Unit Vector When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. A matrix a ∈ gl. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every other row. Orthogonal Matrix Unit Vector.
From www.youtube.com
Ex Find Two Unit Vectors Orthogonal to Two Given Vectors YouTube Orthogonal Matrix Unit Vector Understand the relationship between the dot. A set is orthonormal if it is orthogonal and each vector is a unit vector. An orthonormal basis is a basis whose vectors are. The precise definition is as follows. An orthogonal matrix \(u\), from definition 4.11.7 , is one in which \(uu^{t}. When an \(n \times n\) matrix has all real entries and. Orthogonal Matrix Unit Vector.