The Set Of Complex Numbers Closed Under Multiplication . Apparently we don’t need to. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. The set of complex numbers $\c$ forms a ring under addition and multiplication: Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. $\mathbb{r}$ is a field because we have. The complex numbers are closed under addition, subtraction. Recall that complex numbers form field under the operations of. We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. Let $z = a + bi$ and $w. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ.
from www.chegg.com
Recall that complex numbers form field under the operations of. Apparently we don’t need to. The complex numbers are closed under addition, subtraction. We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. The set of complex numbers $\c$ forms a ring under addition and multiplication: There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. $\mathbb{r}$ is a field because we have. Let $z = a + bi$ and $w. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication.
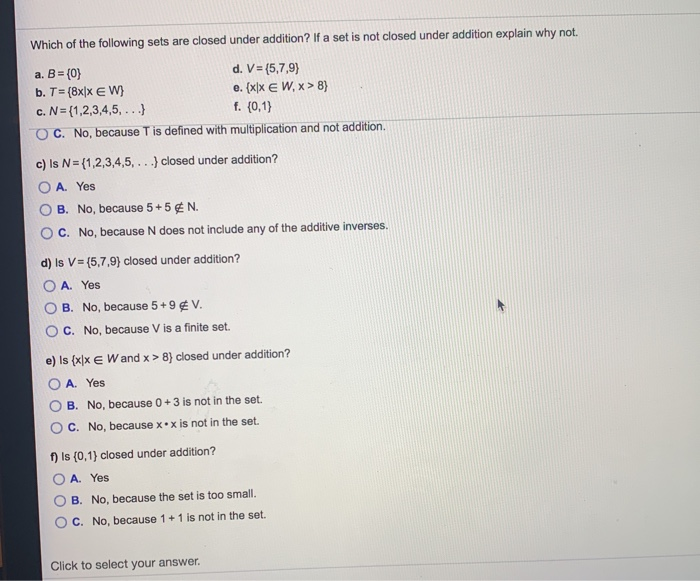
Solved Which of the following sets are closed under
The Set Of Complex Numbers Closed Under Multiplication We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. Let $z = a + bi$ and $w. The set of complex numbers $\c$ forms a ring under addition and multiplication: Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. Apparently we don’t need to. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. Recall that complex numbers form field under the operations of. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: $\mathbb{r}$ is a field because we have. We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. The complex numbers are closed under addition, subtraction.
From www.media4math.com
DefinitionClosure Property Numbers and Closure The Set Of Complex Numbers Closed Under Multiplication Let $z = a + bi$ and $w. $\mathbb{r}$ is a field because we have. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: The complex numbers are closed. The Set Of Complex Numbers Closed Under Multiplication.
From math.stackexchange.com
linear algebra Proving vector subspace is closed on multiplication The Set Of Complex Numbers Closed Under Multiplication If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. Let $z = a + bi$ and $w. Recall that complex numbers form field under the operations of. The set of complex. The Set Of Complex Numbers Closed Under Multiplication.
From thinkzone.wlonk.com
Number Sets The Set Of Complex Numbers Closed Under Multiplication Let $z = a + bi$ and $w. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for. The Set Of Complex Numbers Closed Under Multiplication.
From thinkzone.wlonk.com
Number Sets The Set Of Complex Numbers Closed Under Multiplication Apparently we don’t need to. Let $z = a + bi$ and $w. We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. Recall that complex numbers form field under the operations of. If $\mathbb{r}$ is defined in this manner, then the answer to your question is. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Let's Learn Discrete Math Sets Closed Under Addition and The Set Of Complex Numbers Closed Under Multiplication $\mathbb{r}$ is a field because we have. Apparently we don’t need to. The set of complex numbers $\c$ forms a ring under addition and multiplication: There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. Recall that complex numbers form field under the operations of.. The Set Of Complex Numbers Closed Under Multiplication.
From www.storyofmathematics.com
Closed Under Addition Property, Type of Numbers, and Examples The The Set Of Complex Numbers Closed Under Multiplication There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. $\mathbb{r}$ is a field because we have. The set of complex numbers. The Set Of Complex Numbers Closed Under Multiplication.
From www.houseofmath.com
How to Multiply Complex Numbers The Set Of Complex Numbers Closed Under Multiplication Apparently we don’t need to. The set of complex numbers $\c$ forms a ring under addition and multiplication: The complex numbers are closed under addition, subtraction. Let $z = a + bi$ and $w. We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. Recall that complex numbers form field under the operations. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Q52 Let S be the set of all complex numbers z satisfying z2+i≥√5If The Set Of Complex Numbers Closed Under Multiplication Apparently we don’t need to. The set of complex numbers $\c$ forms a ring under addition and multiplication: $\mathbb{r}$ is a field because we have. Let $z = a + bi$ and $w. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under. The Set Of Complex Numbers Closed Under Multiplication.
From owlcation.com
Math How to Use Complex Numbers and the Complex Plane Owlcation The Set Of Complex Numbers Closed Under Multiplication The set of complex numbers $\c$ forms a ring under addition and multiplication: Apparently we don’t need to. We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. The complex. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Closure Property of Multiplication of Rational Numbers C.B.S.E The Set Of Complex Numbers Closed Under Multiplication If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: Let $z = a + bi$ and $w. $\mathbb{r}$ is a field because we have. We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. Apparently we don’t need to. There are consequences of this fact, namely in. The Set Of Complex Numbers Closed Under Multiplication.
From www.slideserve.com
PPT Trigonometric Form of a Complex Number PowerPoint Presentation The Set Of Complex Numbers Closed Under Multiplication If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. Apparently we don’t need to. Recall that complex numbers form field under the operations of. We first show that $g = \mathbb{c}^*. The Set Of Complex Numbers Closed Under Multiplication.
From www.expii.com
Multiplying Complex Numbers Expii The Set Of Complex Numbers Closed Under Multiplication Recall that complex numbers form field under the operations of. $\mathbb{r}$ is a field because we have. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. The complex numbers are closed under addition, subtraction. Apparently we don’t need to. The set of complex numbers. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Complex numbers with examples Introduction YouTube The Set Of Complex Numbers Closed Under Multiplication There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. Recall that complex numbers form field under the operations of. $\mathbb{r}$ is a field because we have. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: We first show. The Set Of Complex Numbers Closed Under Multiplication.
From www.slideserve.com
PPT Complex numbers PowerPoint Presentation, free download ID2103997 The Set Of Complex Numbers Closed Under Multiplication Recall that complex numbers form field under the operations of. The set of complex numbers $\c$ forms a ring under addition and multiplication: There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. If $\mathbb{r}$ is defined in this manner, then the answer to your. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Closure Property Multiplication of Whole Numbers YouTube The Set Of Complex Numbers Closed Under Multiplication $\mathbb{r}$ is a field because we have. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. The set of complex numbers. The Set Of Complex Numbers Closed Under Multiplication.
From www.bartleby.com
Answered Which of the following sets are closed… bartleby The Set Of Complex Numbers Closed Under Multiplication If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: $\mathbb{r}$ is a field because we have. Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Group Theory 5a Complex numbers under multiplication YouTube The Set Of Complex Numbers Closed Under Multiplication Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: The complex numbers are closed under addition, subtraction. There are consequences of this fact, namely in showing that the set of all. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Multiplication of Complex Numbers YouTube The Set Of Complex Numbers Closed Under Multiplication The set of complex numbers $\c$ forms a ring under addition and multiplication: Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. Recall that complex numbers form field under the operations of. There are consequences of this fact, namely in showing that the set of all. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Abstract Algebra 11 The group of nonzero real numbers under The Set Of Complex Numbers Closed Under Multiplication $\mathbb{r}$ is a field because we have. Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. Recall that complex numbers form. The Set Of Complex Numbers Closed Under Multiplication.
From youtube.com
How to Prove the set of Rational numbers is Closed Over Addition YouTube The Set Of Complex Numbers Closed Under Multiplication Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: Let $z = a + bi$ and $w. Apparently we don’t need to. Recall that complex numbers form field under the operations. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Properties of the set of rational numbers under multiplication The Set Of Complex Numbers Closed Under Multiplication We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. The set of complex numbers $\c$ forms a ring under addition and multiplication: The complex numbers are closed under addition, subtraction. Let $z = a + bi$ and $w. If $\mathbb{r}$ is defined in this manner, then. The Set Of Complex Numbers Closed Under Multiplication.
From materialcampuseburnean.z21.web.core.windows.net
Multiplying Complex Numbers Practice The Set Of Complex Numbers Closed Under Multiplication If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: Let $z = a + bi$ and $w. We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for. The Set Of Complex Numbers Closed Under Multiplication.
From www.chegg.com
Solved Let C* be the set of nonzero complex numbers, which The Set Of Complex Numbers Closed Under Multiplication The set of complex numbers $\c$ forms a ring under addition and multiplication: Recall that complex numbers form field under the operations of. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. Apparently we don’t need to. Let $z = a + bi$ and. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Determine if a set is closed under scalar multiplication Linear The Set Of Complex Numbers Closed Under Multiplication $\mathbb{r}$ is a field because we have. Let $z = a + bi$ and $w. We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. The set of complex numbers $\c$ forms a ring under addition and multiplication: Apparently we don’t need to. If $\mathbb{r}$ is defined in this manner, then the answer. The Set Of Complex Numbers Closed Under Multiplication.
From www.onlinemathlearning.com
Multiplying Complex Numbers (examples, solutions, videos, worksheets The Set Of Complex Numbers Closed Under Multiplication Recall that complex numbers form field under the operations of. The set of complex numbers $\c$ forms a ring under addition and multiplication: Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. Apparently we don’t need to. Let $z = a + bi$ and $w. The. The Set Of Complex Numbers Closed Under Multiplication.
From www.slideshare.net
Math 4 axioms on the set of real numbers The Set Of Complex Numbers Closed Under Multiplication The complex numbers are closed under addition, subtraction. Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: The set of complex numbers $\c$ forms a ring under addition and multiplication: Apparently. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Determine whether a set is closed or open YouTube The Set Of Complex Numbers Closed Under Multiplication Let $z = a + bi$ and $w. Recall that complex numbers form field under the operations of. Apparently we don’t need to. Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. We can see need for complex numbers by looking at the shortcomings of all. The Set Of Complex Numbers Closed Under Multiplication.
From www.numerade.com
SOLVEDDecide whether the indicated operations of addition and The Set Of Complex Numbers Closed Under Multiplication Apparently we don’t need to. The complex numbers are closed under addition, subtraction. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: Recall that complex numbers form field under the operations of. The set of complex numbers $\c$ forms a ring under addition and multiplication: There are consequences of this fact, namely in showing. The Set Of Complex Numbers Closed Under Multiplication.
From www.numerade.com
SOLVED Draw the following sets of complex numbers in the complex plane The Set Of Complex Numbers Closed Under Multiplication Recall that complex numbers form field under the operations of. The set of complex numbers $\c$ forms a ring under addition and multiplication: $\mathbb{r}$ is a field because we have. Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. Let $z = a + bi$ and. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Multiplication with Complex Numbers YouTube The Set Of Complex Numbers Closed Under Multiplication Let $z = a + bi$ and $w. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. Recall that complex numbers form field under the operations of. Apparently we. The Set Of Complex Numbers Closed Under Multiplication.
From saylordotorg.github.io
Complex Numbers and Their Operations The Set Of Complex Numbers Closed Under Multiplication We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. Let $z = a + bi$ and $w. The complex numbers are closed under addition, subtraction. If $\mathbb{r}$. The Set Of Complex Numbers Closed Under Multiplication.
From www.scribd.com
The Set of Complex Numbers The Set Of Complex Numbers Closed Under Multiplication The complex numbers are closed under addition, subtraction. $\mathbb{r}$ is a field because we have. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for r ∈ ∈ r ℜ. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: The set of complex numbers. The Set Of Complex Numbers Closed Under Multiplication.
From www.youtube.com
Closed Sets Multiples of 3 YouTube The Set Of Complex Numbers Closed Under Multiplication We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under complex multiplication forms a group. We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. There are consequences of this fact, namely in showing that the set of all pure imaginary complex numbers ri for. The Set Of Complex Numbers Closed Under Multiplication.
From www.chegg.com
Solved Which of the following sets are closed under The Set Of Complex Numbers Closed Under Multiplication We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. Recall that complex numbers form field under the operations of. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: We first show that $g = \mathbb{c}^* = \mathbb{c} − \{0\}$ under. The Set Of Complex Numbers Closed Under Multiplication.
From www.toppr.com
Basics of Complex Numbers Equality, Root, Powers of Iota with Examples The Set Of Complex Numbers Closed Under Multiplication We can see need for complex numbers by looking at the shortcomings of all the simpler (more obvious) number systems that preceded them. The complex numbers are closed under addition, subtraction. If $\mathbb{r}$ is defined in this manner, then the answer to your question is trivial: Since the sum and product of complex numbers are complex numbers, we say that. The Set Of Complex Numbers Closed Under Multiplication.