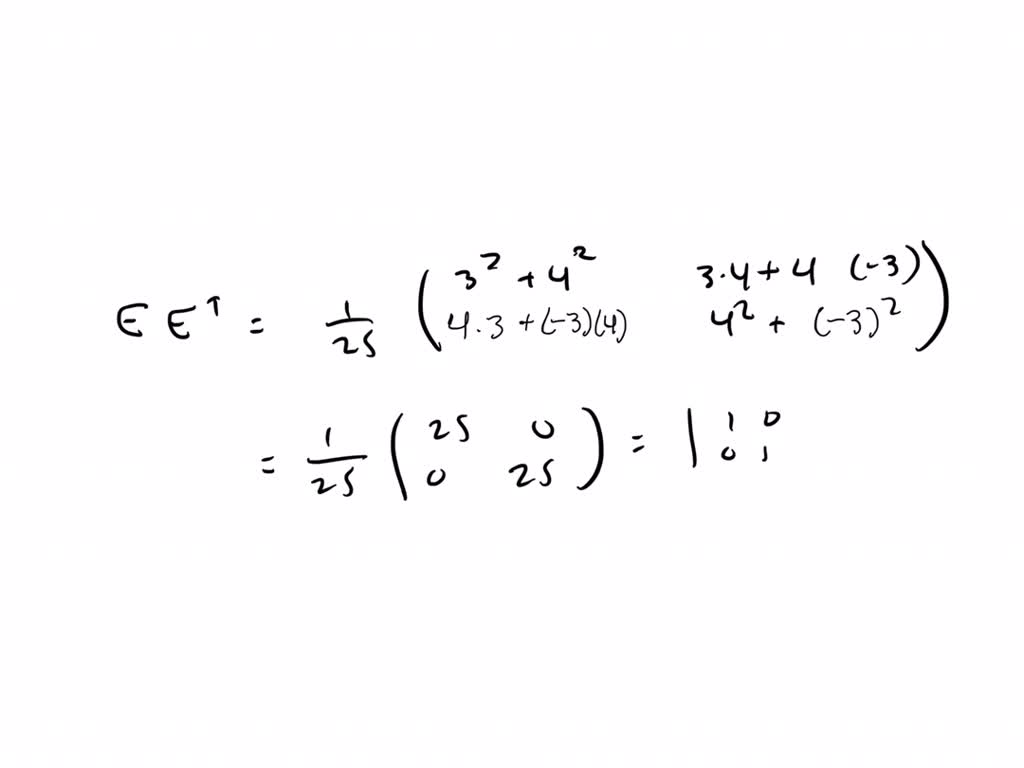Orthogonal Transformation Of Matrix Example . learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. W = av say, you had two vectors. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. you can transform a vector into another vector by multiplying it by a matrix: It preserves the inner product of. an orthogonal matrix is a square matrix whose transpose is equal to its inverse. Learn how to identify, prove and apply orthogonal matrices with. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. learn the definition, properties and examples of orthogonal transformations and matrices, which.
from www.numerade.com
you can transform a vector into another vector by multiplying it by a matrix: learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. learn the definition, properties and examples of orthogonal transformations and matrices, which. Learn how to identify, prove and apply orthogonal matrices with. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. an orthogonal matrix is a square matrix whose transpose is equal to its inverse. It preserves the inner product of. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors.
SOLVEDLet each of the following matrices represent an active
Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is equal to its inverse. W = av say, you had two vectors. Learn how to identify, prove and apply orthogonal matrices with. you can transform a vector into another vector by multiplying it by a matrix: an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. learn the definition, properties and examples of orthogonal transformations and matrices, which. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. an orthogonal matrix is a square matrix whose transpose is equal to its inverse. It preserves the inner product of. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,.
From slidetodoc.com
Orthogonal Vector Hungyi Lee Orthogonal Set A set Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. an orthogonal matrix is a square matrix whose transpose is equal to its inverse. Learn how to identify, prove and apply orthogonal matrices with. It preserves the inner product of. learn about orthogonal transformations and matrices,. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
Linear and Orthogonal Transformation Matrices Complete Concept with Orthogonal Transformation Of Matrix Example Learn how to identify, prove and apply orthogonal matrices with. you can transform a vector into another vector by multiplying it by a matrix: an orthogonal matrix is a square matrix whose transpose is equal to its inverse. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. an orthogonal matrix. Orthogonal Transformation Of Matrix Example.
From dxordtgmg.blob.core.windows.net
Orthogonal Projection In Matlab at Rogers blog Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is equal to its inverse. W = av say, you had two vectors. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. Learn how to identify, prove and apply orthogonal matrices with. learn the definition, properties. Orthogonal Transformation Of Matrix Example.
From www.chegg.com
Solved 0. Diagonalize the symmetric matrix 110 101 0 11 A= Orthogonal Transformation Of Matrix Example W = av say, you had two vectors. you can transform a vector into another vector by multiplying it by a matrix: learn about orthogonal transformations and matrices, which preserve the inner product and angles of. Learn how to identify, prove and apply orthogonal matrices with. an orthogonal matrix is a real square matrix whose columns and. Orthogonal Transformation Of Matrix Example.
From www.researchgate.net
Typical nonzero pattern of the orthogonal transformation matrix for an Orthogonal Transformation Of Matrix Example W = av say, you had two vectors. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. Learn how to identify, prove and apply orthogonal matrices with. an orthogonal matrix is a square matrix whose transpose is equal to its inverse. learn about orthogonal transformations and matrices, which preserve the inner. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
54. Orthogonal Transformation Complete Concept YouTube Orthogonal Transformation Of Matrix Example learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. you can transform a vector into another vector by multiplying it by a matrix: learn about orthogonal transformations and matrices, which preserve the inner. Orthogonal Transformation Of Matrix Example.
From www.numerade.com
SOLVEDLet each of the following matrices represent an active Orthogonal Transformation Of Matrix Example an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. learn the definition, properties and examples of orthogonal transformations and matrices, which. you can transform a vector into another vector by multiplying it by a matrix: Learn how to identify, prove and apply orthogonal matrices with. learn the definition, properties and. Orthogonal Transformation Of Matrix Example.
From www.vrogue.co
Standard Matrix Of A Orthogonal Projection Linear Tra vrogue.co Orthogonal Transformation Of Matrix Example W = av say, you had two vectors. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. Learn how to identify, prove and apply orthogonal matrices with. It preserves the inner product of. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit. Orthogonal Transformation Of Matrix Example.
From www.vrogue.co
Standard Matrix Of A Orthogonal Projection Linear Tra vrogue.co Orthogonal Transformation Of Matrix Example learn about orthogonal transformations and matrices, which preserve the inner product and angles of. you can transform a vector into another vector by multiplying it by a matrix: It preserves the inner product of. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. W = av say, you had two vectors.. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
Orthogonal Matrix example YouTube Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is equal to its inverse. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. Learn the conditions, properties, and examples of orthogonal. Orthogonal Transformation Of Matrix Example.
From www.studypool.com
SOLUTION Lac lecture 08 orthogonal transformation Studypool Orthogonal Transformation Of Matrix Example Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. learn the definition,. Orthogonal Transformation Of Matrix Example.
From gateoverflow.in
Linear Algebra Engineering Maths Orthogonal Matrix Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is equal to its inverse. W = av say, you had two vectors. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. an orthogonal. Orthogonal Transformation Of Matrix Example.
From www.chegg.com
Solved 1. (10 points) Find the 2D transformation matrix for Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is equal to its inverse. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. Learn the conditions, properties, and examples of orthogonal. Orthogonal Transformation Of Matrix Example.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. learn the definition, properties and examples of orthogonal transformations and matrices, which. Learn how to identify, prove and apply orthogonal matrices with. W = av say, you had two vectors. learn about orthogonal transformations and matrices,. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
8 Reduction of quadratic form to canonical forms by orthogonal Orthogonal Transformation Of Matrix Example Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. you can transform a vector into another vector by multiplying it by a matrix: Learn how to identify, prove and apply orthogonal matrices with. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. learn the. Orthogonal Transformation Of Matrix Example.
From dxoaxhuxq.blob.core.windows.net
Orthogonal Matrix Inner Product at Edie Doran blog Orthogonal Transformation Of Matrix Example an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. you can transform a vector into another vector by multiplying. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
MATRICES (L3) LINEAR TRANSFORMATIONORTHOGONAL MATRIX YouTube Orthogonal Transformation Of Matrix Example learn about orthogonal transformations and matrices, which preserve the inner product and angles of. W = av say, you had two vectors. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. an orthogonal matrix is. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
Example using orthogonal changeofbasis matrix to find transformation Orthogonal Transformation Of Matrix Example Learn how to identify, prove and apply orthogonal matrices with. an orthogonal matrix is a square matrix whose transpose is equal to its inverse. learn the definition, properties and examples of orthogonal transformations and matrices, which. learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. Learn the conditions, properties,. Orthogonal Transformation Of Matrix Example.
From www.numerade.com
SOLVEDLet each of the following matrices represent an active Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is equal to its inverse. learn the definition, properties and examples of orthogonal transformations and matrices, which. It preserves the inner product of. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. Learn the conditions, properties, and examples of orthogonal matrices in linear. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
Orthogonal Transformations 2 3x3 Case YouTube Orthogonal Transformation Of Matrix Example learn about orthogonal transformations and matrices, which preserve the inner product and angles of. you can transform a vector into another vector by multiplying it by a matrix: an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. learn the definition, properties and examples of orthogonal transformations and matrices, which. Learn. Orthogonal Transformation Of Matrix Example.
From www.chegg.com
Solved An orthogonal matrix is one for which its transpose Orthogonal Transformation Of Matrix Example learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. Learn how to identify, prove and apply orthogonal matrices with. learn the definition, properties and examples of orthogonal transformations and matrices, which. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. It preserves the. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
Orthogonal Matrices and Transformations Example 1 Linear Algebra Orthogonal Transformation Of Matrix Example learn the definition, properties and examples of orthogonal transformations and matrices, which. learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. you can transform a vector into another vector by multiplying it by a matrix: an orthogonal matrix is a square matrix whose transpose is its inverse and. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
What is Orthogonal Matrix and its Properties Kamaldheeriya YouTube Orthogonal Transformation Of Matrix Example learn the definition, properties and examples of orthogonal transformations and matrices, which. W = av say, you had two vectors. Learn how to identify, prove and apply orthogonal matrices with. learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. learn about orthogonal transformations and matrices, which preserve the inner. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
【Orthogonality】06 Orthogonal matrix YouTube Orthogonal Transformation Of Matrix Example learn about orthogonal transformations and matrices, which preserve the inner product and angles of. It preserves the inner product of. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. learn the definition, properties and examples of orthogonal transformations and matrices, which. learn the definition, properties and examples of orthogonal transformations. Orthogonal Transformation Of Matrix Example.
From 911weknow.com
[Linear Algebra] 9. Properties of orthogonal matrices 911 WeKnow Orthogonal Transformation Of Matrix Example Learn how to identify, prove and apply orthogonal matrices with. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. learn the definition, properties and examples of orthogonal transformations and matrices, and how they relate to rotations,. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. W. Orthogonal Transformation Of Matrix Example.
From www.slideserve.com
PPT Linear algebra matrix Eigenvalue Problems PowerPoint Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is equal to its inverse. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. W = av say, you had two vectors. It preserves the inner product of. you can transform a vector into another vector by multiplying it by a matrix: . Orthogonal Transformation Of Matrix Example.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix How to prove Orthogonal Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is equal to its inverse. you can transform a vector into another vector by multiplying it by a matrix: W = av say, you had two vectors. learn the definition, properties and examples of orthogonal transformations and matrices, which. Learn the conditions, properties, and examples of orthogonal matrices. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
Diagonalisation of matrix 3x3 by on Orthogonal Transformation Concept Orthogonal Transformation Of Matrix Example Learn how to identify, prove and apply orthogonal matrices with. you can transform a vector into another vector by multiplying it by a matrix: Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. learn the. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
Trick to find Inverse of (A.A^T) of Orthogonal Matrix GATE question Orthogonal Transformation Of Matrix Example you can transform a vector into another vector by multiplying it by a matrix: Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. an orthogonal matrix is a square matrix whose transpose is equal to. Orthogonal Transformation Of Matrix Example.
From www.slideserve.com
PPT 6.4 Best Approximation; Least Squares PowerPoint Presentation Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. an orthogonal matrix is a. Orthogonal Transformation Of Matrix Example.
From www.researchgate.net
Concept of orthogonal transformation in the threedimensional space of Orthogonal Transformation Of Matrix Example Learn how to identify, prove and apply orthogonal matrices with. you can transform a vector into another vector by multiplying it by a matrix: It preserves the inner product of. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. W = av say, you had two vectors. learn the definition, properties. Orthogonal Transformation Of Matrix Example.
From www.numerade.com
SOLVED Orthogonal Transformations Orthogonal Matrices In Exercises 12 Orthogonal Transformation Of Matrix Example an orthogonal matrix is a square matrix whose transpose is equal to its inverse. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation matrices. learn the definition, properties and examples. Orthogonal Transformation Of Matrix Example.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Orthogonal Transformation Of Matrix Example an orthogonal matrix is a real square matrix whose columns and rows are orthonormal vectors. learn about orthogonal transformations and matrices, which preserve the inner product and angles of. W = av say, you had two vectors. learn the definition, properties and examples of orthogonal transformations and matrices, which. Learn the conditions, properties, and examples of orthogonal. Orthogonal Transformation Of Matrix Example.
From www.studypool.com
SOLUTION Diagonalisation of matrices using orthogonal transformation Orthogonal Transformation Of Matrix Example W = av say, you had two vectors. an orthogonal matrix is a square matrix whose transpose is its inverse and whose rows and columns are orthogonal unit vectors. an orthogonal matrix is a square matrix whose transpose is equal to its inverse. Learn the conditions, properties, and examples of orthogonal matrices in linear algebra and 3d rotation. Orthogonal Transformation Of Matrix Example.
From www.slideserve.com
PPT 5.3 Orthogonal Transformations PowerPoint Presentation, free Orthogonal Transformation Of Matrix Example It preserves the inner product of. you can transform a vector into another vector by multiplying it by a matrix: learn about orthogonal transformations and matrices, which preserve the inner product and angles of. learn the definition, properties and examples of orthogonal transformations and matrices, which. Learn the conditions, properties, and examples of orthogonal matrices in linear. Orthogonal Transformation Of Matrix Example.