Tree Or Graph Example . Trees and graphs (explained) a journey through graph theory. For example, the graph in figure 12.206 is not a tree, but it contains two components, one. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Master the art of trees and graphs—unlock the mysteries of graph. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. A \(k_2\) is a tree. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees.
from www.youtube.com
Master the art of trees and graphs—unlock the mysteries of graph. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. Trees and graphs (explained) a journey through graph theory. A \(k_2\) is a tree. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. For example, the graph in figure 12.206 is not a tree, but it contains two components, one. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions:
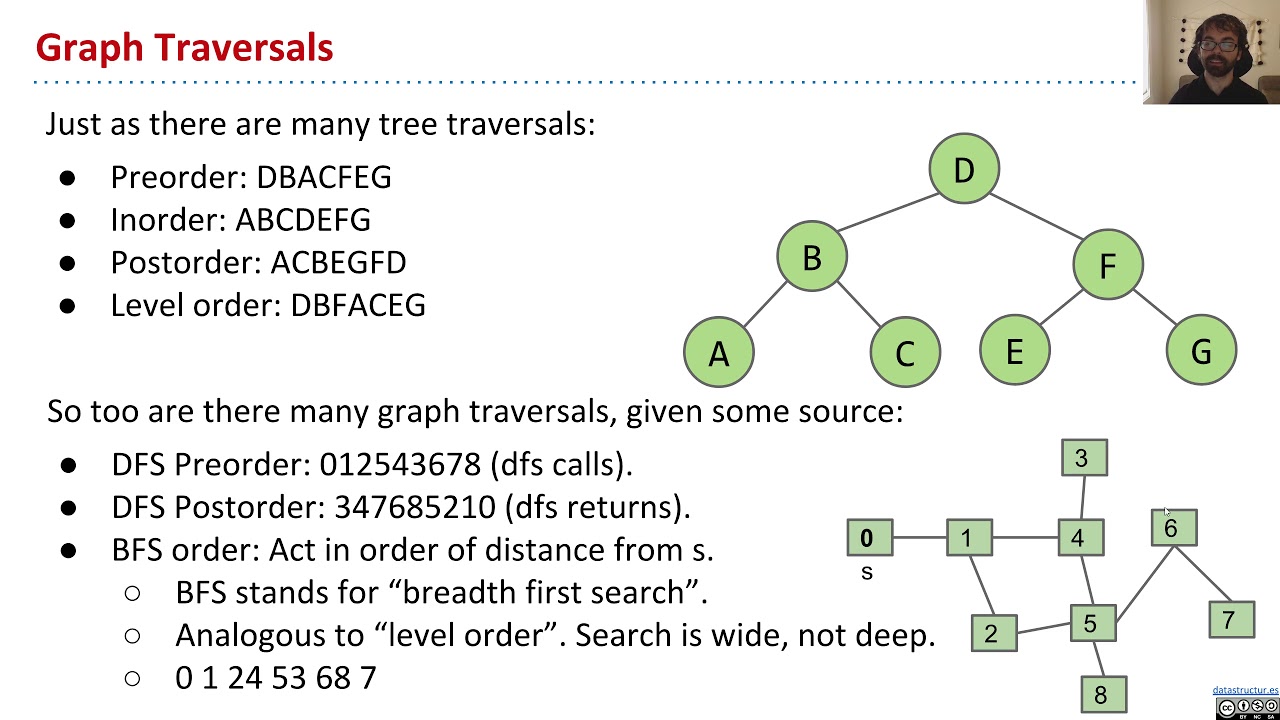
Intro to Graphs, Video 6 Tree vs Graph Traversals YouTube
Tree Or Graph Example Trees and graphs (explained) a journey through graph theory. Master the art of trees and graphs—unlock the mysteries of graph. Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. For example, the graph in figure 12.206 is not a tree, but it contains two components, one. Trees and graphs (explained) a journey through graph theory. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. A \(k_2\) is a tree. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own.
From www.statology.org
How to Fit Classification and Regression Trees in R Tree Or Graph Example However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. For example, the graph in figure 12.206 is not a. Tree Or Graph Example.
From calcworkshop.com
Tree Graph (How To w/ 11+ StepbyStep Examples!) Tree Or Graph Example Master the art of trees and graphs—unlock the mysteries of graph. For example, the graph in figure 12.206 is not a tree, but it contains two components, one. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. For example, the graph in figure 12.234 is not a tree, but. Tree Or Graph Example.
From stackoverflow.com
Undirected graph conversion to tree Stack Overflow Tree Or Graph Example For example, the graph in figure 12.206 is not a tree, but it contains two components, one. Master the art of trees and graphs—unlock the mysteries of graph. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. A \(k_2\) is a tree. Mathematicians have had a lot of fun. Tree Or Graph Example.
From www.slideserve.com
PPT Graph Theory (Trees) PowerPoint Presentation, free download ID Tree Or Graph Example Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. A \(k_2\) is a tree. For example, the graph in figure 12.234 is not. Tree Or Graph Example.
From www.slideserve.com
PPT H. Rosen Chapter 8 Trees PowerPoint Presentation, free Tree Or Graph Example A \(k_2\) is a tree. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Trees and graphs (explained) a journey through graph theory. However, if \(n\geq 3\text{,}\) a \(k_n\). Tree Or Graph Example.
From templates.rjuuc.edu.np
Tree Graph Template Tree Or Graph Example Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. A \(k_2\) is a tree. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be. Tree Or Graph Example.
From slides.com
Introduction to Trees and Graphs Tree Or Graph Example A \(k_2\) is a tree. Master the art of trees and graphs—unlock the mysteries of graph. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Trees and graphs (explained). Tree Or Graph Example.
From calcworkshop.com
Tree Graph (How To w/ 11+ StepbyStep Examples!) Tree Or Graph Example Trees and graphs (explained) a journey through graph theory. A \(k_2\) is a tree. Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. Master the art of trees and graphs—unlock the mysteries of graph. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices. Tree Or Graph Example.
From www.baeldung.com
Tree vs Graph Data Structure Baeldung on Computer Science Tree Or Graph Example For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Master the art of trees and graphs—unlock the mysteries of graph. For example, the graph in figure 12.206 is not. Tree Or Graph Example.
From www.youtube.com
Rooting a tree Graph Theory YouTube Tree Or Graph Example For example, the graph in figure 12.206 is not a tree, but it contains two components, one. A \(k_2\) is a tree. Trees and graphs (explained) a journey through graph theory. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: For example, the. Tree Or Graph Example.
From www.interviewkickstart.com
Graph Theory Trees Tree Or Graph Example Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. A \(k_2\) is a tree. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be. Tree Or Graph Example.
From www.cuemath.com
Bar Graph Definition, Examples, Types How to Make Bar Graphs? Tree Or Graph Example For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Master the art of trees and graphs—unlock the mysteries of graph. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a. Tree Or Graph Example.
From towardsdatascience.com
8 Useful Tree Data Structures Worth Knowing Towards Data Science Tree Or Graph Example For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: For example, the graph. Tree Or Graph Example.
From www.edrawsoft.com
How to Create A Tree Chart Edraw Tree Or Graph Example For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Master the art of trees and graphs—unlock the mysteries of graph. For example, the graph in figure 12.206 is not. Tree Or Graph Example.
From templates.rjuuc.edu.np
Tree Graph Template Tree Or Graph Example Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. Master the art of trees and graphs—unlock the mysteries of graph. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which. Tree Or Graph Example.
From codesandbox.io
reacttreegraph examples CodeSandbox Tree Or Graph Example Trees and graphs (explained) a journey through graph theory. Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. For example, the graph in figure 12.206 is not a tree, but it contains two components, one. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are. Tree Or Graph Example.
From calcworkshop.com
Tree Graph (How To w/ 11+ StepbyStep Examples!) Tree Or Graph Example However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. For example, the graph in figure 12.206 is not a tree, but it contains two components, one. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: For example, the graph in figure 12.234 is not a tree, but it contains two components, one. Tree Or Graph Example.
From www.cuemath.com
Bar Graph / Bar Chart Cuemath Tree Or Graph Example [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. Master the art of trees and graphs—unlock the mysteries of graph. For example, the graph in figure 12.206 is not a tree, but it contains two components, one.. Tree Or Graph Example.
From www.youtube.com
Tree (graph theory) YouTube Tree Or Graph Example For example, the graph in figure 12.206 is not a tree, but it contains two components, one. Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. A \(k_2\) is a tree. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: However, if \(n\geq 3\text{,}\) a \(k_n\). Tree Or Graph Example.
From ptwiddle.github.io
Lecture 6 Trees Tree Or Graph Example A \(k_2\) is a tree. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its. Tree Or Graph Example.
From codingsight.com
Comparison of Tree Graphs Tree Or Graph Example However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. For example, the graph in figure 12.206 is not a tree, but it contains two components, one. Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. Master the art of trees and graphs—unlock the mysteries of graph. Graphs i, ii and iii in. Tree Or Graph Example.
From courses.cs.washington.edu
Trees as Graphs Tree Or Graph Example For example, the graph in figure 12.206 is not a tree, but it contains two components, one. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. Master the art of trees and graphs—unlock. Tree Or Graph Example.
From www.youtube.com
Intro to Graphs, Video 6 Tree vs Graph Traversals YouTube Tree Or Graph Example Master the art of trees and graphs—unlock the mysteries of graph. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. A \(k_2\) is a tree. Trees and graphs (explained) a journey through graph theory. For example, the graph in figure 12.206 is not a tree, but it contains two components, one. [edit] a tree is an undirected graph g. Tree Or Graph Example.
From www.youtube.com
Tree center(s) Graph Theory YouTube Tree Or Graph Example Master the art of trees and graphs—unlock the mysteries of graph. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. Trees and graphs (explained) a journey through graph theory. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g,. Tree Or Graph Example.
From calcworkshop.com
Tree Graph (How To w/ 11+ StepbyStep Examples!) Tree Or Graph Example Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. A \(k_2\) is a tree. Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. For example, the graph in figure 12.206 is not a tree, but it contains two components, one. [edit] a. Tree Or Graph Example.
From slides.com
Introduction to Trees and Graphs Tree Or Graph Example Master the art of trees and graphs—unlock the mysteries of graph. Trees and graphs (explained) a journey through graph theory. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a. Tree Or Graph Example.
From slides.com
Introduction to Trees and Graphs Tree Or Graph Example For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Master the art of trees and graphs—unlock the mysteries of graph. For example, the graph in figure 12.206 is not. Tree Or Graph Example.
From www.interviewkickstart.com
Graph Theory Trees Tree Or Graph Example A \(k_2\) is a tree. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Trees and graphs (explained) a journey through graph theory. Graphs i, ii and iii in. Tree Or Graph Example.
From juudy.heroinewarrior.com
Introduction to Tree Data Structure and Algorithm Tutorials Tree Or Graph Example Trees and graphs (explained) a journey through graph theory. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. For example, the graph in figure 12.234 is not a tree, but it contains two. Tree Or Graph Example.
From calcworkshop.com
Tree Graph (How To w/ 11+ StepbyStep Examples!) Tree Or Graph Example A \(k_2\) is a tree. Mathematicians have had a lot of fun naming graphs that are trees or that contain trees. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. Trees and graphs (explained) a journey through graph theory. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree.. Tree Or Graph Example.
From www.simplilearn.com
What Is Spanning Tree in Data Structure with Examples Simplilearn Tree Or Graph Example For example, the graph in figure 12.206 is not a tree, but it contains two components, one. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its own. Mathematicians have had. Tree Or Graph Example.
From www.youtube.com
Properties of Trees in Graph TheoryEngineering Maths YouTube Tree Or Graph Example Master the art of trees and graphs—unlock the mysteries of graph. Trees and graphs (explained) a journey through graph theory. A \(k_2\) is a tree. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices. Tree Or Graph Example.
From www.jointjs.com
Tree Graphs Demo applications & examples Tree Or Graph Example For example, the graph in figure 12.206 is not a tree, but it contains two components, one. Trees and graphs (explained) a journey through graph theory. Master the art of trees and graphs—unlock the mysteries of graph. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. [edit] a tree. Tree Or Graph Example.
From www.fa17.eecs70.org
Graph Theory Tree Or Graph Example Master the art of trees and graphs—unlock the mysteries of graph. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. For example, the graph in figure 12.234 is not a tree, but it contains two components, one containing vertices a through d, and the other containing vertices e through g, each of which would be a tree on its. Tree Or Graph Example.
From www.slideshare.net
Tree Connected, undirected, acyclic graph Tree Or Graph Example Trees and graphs (explained) a journey through graph theory. Graphs i, ii and iii in figure \(\pageindex{1}\) are all trees, while graphs iv, v, and vi are not trees. However, if \(n\geq 3\text{,}\) a \(k_n\) is not a tree. [edit] a tree is an undirected graph g that satisfies any of the following equivalent conditions: For example, the graph in. Tree Or Graph Example.