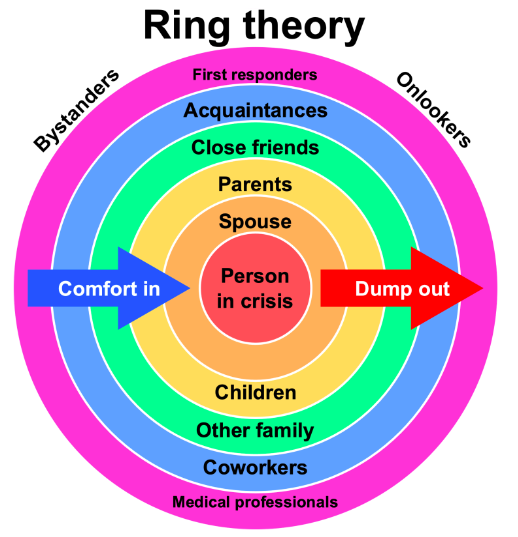
Ring Theory Purpose . A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: Generally the rings we consider will not necessarily have an identity or be commutative. We assume knowledge of the notations of. X(y + z) = xy +. A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). If 1 = 0, then the ring consists of one element 0; This volume contains the proceedings of the ring theory session in honor of t. Almost all interesting associative rings do have identities. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties:
from sudc.org
X(y + z) = xy +. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: We assume knowledge of the notations of. This volume contains the proceedings of the ring theory session in honor of t. A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). Almost all interesting associative rings do have identities. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: Generally the rings we consider will not necessarily have an identity or be commutative. If 1 = 0, then the ring consists of one element 0;
Understanding Ring Theory A Guide to Compassionate Support in
Ring Theory Purpose A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). Almost all interesting associative rings do have identities. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: We assume knowledge of the notations of. If 1 = 0, then the ring consists of one element 0; Generally the rings we consider will not necessarily have an identity or be commutative. This volume contains the proceedings of the ring theory session in honor of t. X(y + z) = xy +.
From abeautifulvoice.org
The Ring Theory When It's Not About You A Beautiful Voice Ring Theory Purpose A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: If 1 = 0, then the ring consists of one element 0; Almost. Ring Theory Purpose.
From www.santafenewmexican.com
Supporting a friend or loved one Cancer Resource Guide Ring Theory Purpose Generally the rings we consider will not necessarily have an identity or be commutative. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \. Ring Theory Purpose.
From www.academia.edu
(PDF) Ring Theory A Tool for Conflict Analysis and the Design Ring Theory Purpose A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: We assume knowledge of the notations of. This volume contains the proceedings of the ring theory session in honor of t. A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and. Ring Theory Purpose.
From www.youtube.com
Characteristic of a ring/ring theory /PPSC preperation /Lecture 20 Ring Theory Purpose We assume knowledge of the notations of. X(y + z) = xy +. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: This volume contains the proceedings of the ring theory session in honor of t. A ring is a set equipped with two operations (usually referred to as addition and. Ring Theory Purpose.
From www.youtube.com
RING THEORY 10 MAXIMAL IDEAL IN A RING, QUOTIENT RING NA Math Study Ring Theory Purpose We assume knowledge of the notations of. A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). Almost all interesting associative rings do have identities. Generally the rings we consider will not necessarily have an identity or be commutative. This volume. Ring Theory Purpose.
From www.youtube.com
Types of Ring /Ring theory /PPSC preperation /Lecture 18 YouTube Ring Theory Purpose We assume knowledge of the notations of. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). Generally the rings we. Ring Theory Purpose.
From sudc.org
Understanding Ring Theory A Guide to Compassionate Support in Ring Theory Purpose X(y + z) = xy +. Generally the rings we consider will not necessarily have an identity or be commutative. We assume knowledge of the notations of. If 1 = 0, then the ring consists of one element 0; A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: A. Ring Theory Purpose.
From www.youtube.com
lec 18 advanced ring theory 1 definition of ideal and its examples Ring Theory Purpose A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: Almost all interesting associative rings do have identities. If 1 =. Ring Theory Purpose.
From www.youtube.com
lec 21 Advanced ring theory 1 definition of radical class examples and Ring Theory Purpose A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). X(y + z) = xy +. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: If 1 = 0, then. Ring Theory Purpose.
From www.youtube.com
RING THEORY 2 EXAMPLE OF RING ,TRIVIAL RING ,NONTRIVIAL RING NA Ring Theory Purpose Generally the rings we consider will not necessarily have an identity or be commutative. We assume knowledge of the notations of. Almost all interesting associative rings do have identities. X(y + z) = xy +. A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary. Ring Theory Purpose.
From www.youtube.com
Ring TheoryBasic concepts and definition of Ring (Lecture01) YouTube Ring Theory Purpose Generally the rings we consider will not necessarily have an identity or be commutative. This volume contains the proceedings of the ring theory session in honor of t. We assume knowledge of the notations of. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: If 1 = 0, then the ring. Ring Theory Purpose.
From studylib.net
Ring Theory Ring Theory Purpose A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: This volume contains the proceedings of the ring theory session in honor of t. We assume knowledge of the notations of. X(y + z) = xy +. A ring is a set equipped with two operations (usually referred to as addition and. Ring Theory Purpose.
From www.youtube.com
lec 10 part 1 advanced ring theory 1 definition of subring and its Ring Theory Purpose Generally the rings we consider will not necessarily have an identity or be commutative. We assume knowledge of the notations of. This volume contains the proceedings of the ring theory session in honor of t. If 1 = 0, then the ring consists of one element 0; Almost all interesting associative rings do have identities. A ring is an additive. Ring Theory Purpose.
From www.psychologytoday.com
Ring Theory Helps Us Bring Comfort In Psychology Today Ring Theory Purpose This volume contains the proceedings of the ring theory session in honor of t. Generally the rings we consider will not necessarily have an identity or be commutative. If 1 = 0, then the ring consists of one element 0; A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties:. Ring Theory Purpose.
From www.learning-mind.com
Ring Theory a Simple Rule to Follow When Confiding Your Problems to Ring Theory Purpose We assume knowledge of the notations of. This volume contains the proceedings of the ring theory session in honor of t. If 1 = 0, then the ring consists of one element 0; A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on. Ring Theory Purpose.
From www.amazon.com
Foundations of Module and Ring Theory A Handbook for Study and Ring Theory Purpose A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). We assume knowledge of the notations of. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: If 1 = 0,. Ring Theory Purpose.
From www.everand.com
Ring Theory, 83 by Louis H. Rowen Ebook Everand Ring Theory Purpose Almost all interesting associative rings do have identities. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: Generally the rings we consider will not necessarily have an identity or be commutative. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law:. Ring Theory Purpose.
From www.youtube.com
Ring theoryll ; Definition of Ring part1 YouTube Ring Theory Purpose This volume contains the proceedings of the ring theory session in honor of t. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: X(y + z) = xy +. Generally the rings we consider will not necessarily have an identity or be commutative. A ring is an additive (abelian). Ring Theory Purpose.
From www.youtube.com
RING THEORY 4 CHARACTERISTIC OF A RING, IDEMPOTENT AND NILPOTENT Ring Theory Purpose A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: We assume knowledge of the notations of. Generally the rings we consider will not necessarily have an identity or be commutative. A. Ring Theory Purpose.
From www.youtube.com
Ideals in ring theory /PPSC preperation /Lecture 21 YouTube Ring Theory Purpose This volume contains the proceedings of the ring theory session in honor of t. X(y + z) = xy +. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \. Ring Theory Purpose.
From www.youtube.com
Ring Theory Field Definition and Example of Field Abstract Ring Theory Purpose We assume knowledge of the notations of. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: This volume contains the proceedings of the ring theory session in honor of t. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: Generally. Ring Theory Purpose.
From www.researchgate.net
The Ring Theory of Personhood (RtoP) [28] Download Scientific Diagram Ring Theory Purpose X(y + z) = xy +. This volume contains the proceedings of the ring theory session in honor of t. Generally the rings we consider will not necessarily have an identity or be commutative. We assume knowledge of the notations of. Almost all interesting associative rings do have identities. If 1 = 0, then the ring consists of one element. Ring Theory Purpose.
From mysweetdumbbrain.substack.com
Does the Ring Theory Work in a Pandemic? Ring Theory Purpose This volume contains the proceedings of the ring theory session in honor of t. We assume knowledge of the notations of. X(y + z) = xy +. Generally the rings we consider will not necessarily have an identity or be commutative. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: A. Ring Theory Purpose.
From www.researchgate.net
(PDF) Some Basic Facts of Ring Theory Ring Theory Purpose A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: This volume contains the proceedings of the ring theory session in honor of t. Almost all interesting associative rings do have identities.. Ring Theory Purpose.
From www.youtube.com
Characteristics of a ring Ring Theory Ritzymaths YouTube Ring Theory Purpose We assume knowledge of the notations of. This volume contains the proceedings of the ring theory session in honor of t. X(y + z) = xy +. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: Almost all interesting associative rings do have identities. A ring is a set equipped with. Ring Theory Purpose.
From research.ctoam.com
Susan Silk's Ring Theory How to Support a Loved One with Cancer Ring Theory Purpose Almost all interesting associative rings do have identities. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: We assume knowledge of the notations of. X(y + z) = xy +. Generally the rings we consider will not necessarily have an identity or be commutative. If 1 = 0, then. Ring Theory Purpose.
From familytreedoula.com
Navigating Pregnancy Loss with the Help of Ring Theory Family Tree Ring Theory Purpose Generally the rings we consider will not necessarily have an identity or be commutative. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: We assume knowledge of the notations of. If 1 = 0, then the ring consists of one element 0; A ring is an additive (abelian) group. Ring Theory Purpose.
From www.penguinmagic.com
Ring Theory by Antoine Thomas DVD Ring Theory Purpose A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: If 1 = 0, then the ring consists of one element 0; X(y + z) = xy +. Generally the rings we consider will not necessarily have an identity or be commutative. This volume contains the proceedings of the ring. Ring Theory Purpose.
From www.researchgate.net
(PDF) Fundamental Notions in Ring Theory Ring Theory Purpose If 1 = 0, then the ring consists of one element 0; X(y + z) = xy +. A ring is a set equipped with two operations (usually referred to as addition and multiplication) that satisfy certain properties: We assume knowledge of the notations of. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying. Ring Theory Purpose.
From www.slideserve.com
PPT Algebra Review PowerPoint Presentation, free download ID1157524 Ring Theory Purpose A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: This volume contains the proceedings of the ring theory session in honor of t. X(y + z) = xy +. Generally the rings we consider will not necessarily have an identity or be commutative. A ring is an ordered triple \ (. Ring Theory Purpose.
From www.youtube.com
Ring Theory and Linear AlgebraI B.Sc(H) Mathematics, DU YouTube Ring Theory Purpose We assume knowledge of the notations of. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: X(y + z) = xy +. If 1 = 0, then the ring consists of one element 0; A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set. Ring Theory Purpose.
From www.youtube.com
Characteristic of a RingIntroductionRing Theory1BscMath(H)2nd Ring Theory Purpose Almost all interesting associative rings do have identities. This volume contains the proceedings of the ring theory session in honor of t. A ring is an additive (abelian) group r with an additional binary operation (multiplication), satisfying the distributive law: We assume knowledge of the notations of. If 1 = 0, then the ring consists of one element 0; A. Ring Theory Purpose.
From www.youtube.com
Ring theory introduction YouTube Ring Theory Purpose A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\) is a set and \ (+\) and \ (\cdot\) are binary operations on \ (r\). Generally the rings we consider will not necessarily have an identity or be commutative. If 1 = 0, then the ring consists of one element 0; Almost all interesting associative rings. Ring Theory Purpose.
From mentalhealthathome.org
Ring Theory Comfort In, Dump Out Mental Health Home Ring Theory Purpose We assume knowledge of the notations of. Almost all interesting associative rings do have identities. This volume contains the proceedings of the ring theory session in honor of t. X(y + z) = xy +. Generally the rings we consider will not necessarily have an identity or be commutative. If 1 = 0, then the ring consists of one element. Ring Theory Purpose.
From www.youtube.com
Ring theory/introduction to rings in abstract algebra YouTube Ring Theory Purpose Generally the rings we consider will not necessarily have an identity or be commutative. If 1 = 0, then the ring consists of one element 0; This volume contains the proceedings of the ring theory session in honor of t. X(y + z) = xy +. A ring is an ordered triple \ ( (r, + ,\cdot)\) where \ (r\). Ring Theory Purpose.