Magnetic Field Inside Current Carrying Wire Varies With R . the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? let's find the expression for the magnetic field inside a straight long wire. the field outside the coils is nearly zero. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. (b) this cutaway shows the magnetic field generated by the current in the solenoid. to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. B = μ0 ∙ itot 2π ∙ r2 ∙ r. The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. The magnetic field should still go in circular.
from www.doubtnut.com
B = μ0 ∙ itot 2π ∙ r2 ∙ r. The magnetic field should still go in circular. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. (b) this cutaway shows the magnetic field generated by the current in the solenoid. the field outside the coils is nearly zero. to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? let's find the expression for the magnetic field inside a straight long wire. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law.
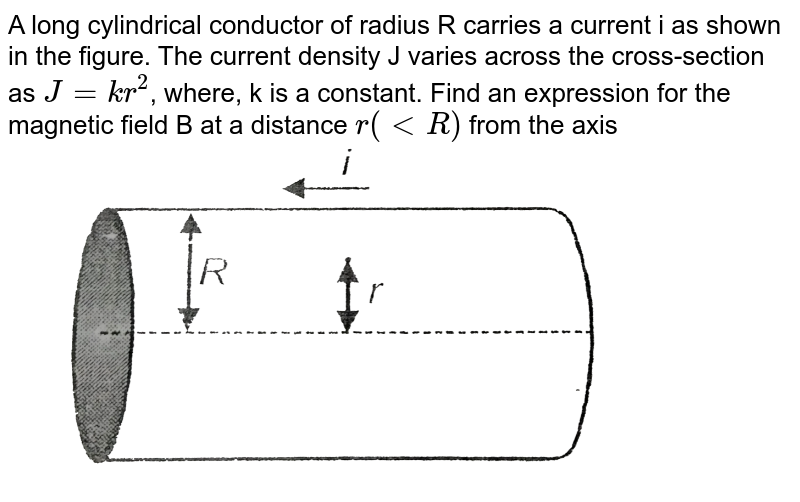
A long cylindrical conductor of radius R carries a current i as shown
Magnetic Field Inside Current Carrying Wire Varies With R what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. the field outside the coils is nearly zero. The magnetic field should still go in circular. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. let's find the expression for the magnetic field inside a straight long wire. B = μ0 ∙ itot 2π ∙ r2 ∙ r. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? (b) this cutaway shows the magnetic field generated by the current in the solenoid.
From www.youtube.com
Force Between Two Parallel Current Carrying Wires, Physics Magnetic Field Inside Current Carrying Wire Varies With R B = μ0 ∙ itot 2π ∙ r2 ∙ r. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? the field outside the coils is nearly zero. to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r.. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.youtube.com
Field due to the Current Carrying Wire of Infinite Length Magnetic Field Inside Current Carrying Wire Varies With R the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. the field outside the coils is nearly zero. to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. The above formula means the magnetic. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.paramhimalaya.com
field patterns produced by currentcarrying conductors Magnetic Field Inside Current Carrying Wire Varies With R The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. to find the magnetic field at a. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.youtube.com
field of a cylindrical conductor carrying uniform current Magnetic Field Inside Current Carrying Wire Varies With R let's find the expression for the magnetic field inside a straight long wire. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? (b) this cutaway shows the magnetic field generated by the current in the solenoid. the magnetic field inside a conductor with uniform current density. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.slideserve.com
PPT Field due to a CurrentCarrying Wire PowerPoint Magnetic Field Inside Current Carrying Wire Varies With R The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. what is the magnetic field due to the current at an. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.chegg.com
Solved A circular loop of radius r carries a current I as Magnetic Field Inside Current Carrying Wire Varies With R The magnetic field should still go in circular. the field outside the coils is nearly zero. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. (b) this cutaway shows the magnetic field generated by the current in the solenoid. the magnetic field. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.electricaltechnology.org
Oersted's Law of Field of a Current Carrying Wire Magnetic Field Inside Current Carrying Wire Varies With R (b) this cutaway shows the magnetic field generated by the current in the solenoid. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop?. Magnetic Field Inside Current Carrying Wire Varies With R.
From physics.stackexchange.com
What is the moments orientation of the free Magnetic Field Inside Current Carrying Wire Varies With R let's find the expression for the magnetic field inside a straight long wire. The magnetic field should still go in circular. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. The above formula means the magnetic field is zero at centre of cross section of the wire. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.doubtnut.com
A long cylindrical conductor of radius R carries a current i as shown Magnetic Field Inside Current Carrying Wire Varies With R the field outside the coils is nearly zero. The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. (b) this cutaway shows the magnetic field generated by the current in the solenoid. let's find the expression for the magnetic field inside. Magnetic Field Inside Current Carrying Wire Varies With R.
From 9to5science.com
[Solved] Electric field around a current carrying 9to5Science Magnetic Field Inside Current Carrying Wire Varies With R to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. the field outside the coils is nearly zero. B = μ0 ∙ itot 2π ∙ r2 ∙ r. let's find the expression for the magnetic field inside a straight long wire. the strength of the magnetic field. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.youtube.com
Field of a Straight Current Carrying Wire YouTube Magnetic Field Inside Current Carrying Wire Varies With R what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. the strength of the magnetic field created by current in a long straight wire is given by \[b. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.slideserve.com
PPT ELECTRODYNAMICS PowerPoint Presentation ID162570 Magnetic Field Inside Current Carrying Wire Varies With R what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. The above formula means the magnetic field is zero at centre of cross section of the wire and. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.dreamstime.com
Field Lines Around a Current Carrying Straight Wire Stock Magnetic Field Inside Current Carrying Wire Varies With R let's find the expression for the magnetic field inside a straight long wire. (b) this cutaway shows the magnetic field generated by the current in the solenoid. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? the strength of the magnetic field created by current in. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.teachoo.com
Field Due to Straight Current Carrying Conductor Teachoo Magnetic Field Inside Current Carrying Wire Varies With R let's find the expression for the magnetic field inside a straight long wire. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. the strength of. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.youtube.com
Ampere's Law field inside a long cylindrical conductor YouTube Magnetic Field Inside Current Carrying Wire Varies With R The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. (b) this cutaway shows the magnetic field generated by the current in the solenoid. The magnetic field should still go in circular. to find the magnetic field at a radius r inside. Magnetic Field Inside Current Carrying Wire Varies With R.
From pressbooks.online.ucf.edu
22.9 Fields Produced by Currents Ampere’s Law College Physics Magnetic Field Inside Current Carrying Wire Varies With R to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. let's find the expression for the magnetic field inside a straight long wire. The magnetic field should still. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.toppr.com
The flux density B at a distance r from a long straight wire Magnetic Field Inside Current Carrying Wire Varies With R what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. The magnetic field should still go in circular. let's find the expression for the magnetic field inside. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.chegg.com
Solved A long, straight wire of radius R carries a current I Magnetic Field Inside Current Carrying Wire Varies With R The magnetic field should still go in circular. (b) this cutaway shows the magnetic field generated by the current in the solenoid. the field outside the coils is nearly zero. let's find the expression for the magnetic field inside a straight long wire. what is the magnetic field due to the current at an arbitrary point p. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.slideserve.com
PPT Chapter 30 Sources of the field PowerPoint Presentation Magnetic Field Inside Current Carrying Wire Varies With R B = μ0 ∙ itot 2π ∙ r2 ∙ r. (b) this cutaway shows the magnetic field generated by the current in the solenoid. to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. what is the magnetic field due to the current at an arbitrary point p along. Magnetic Field Inside Current Carrying Wire Varies With R.
From finwise.edu.vn
List 93+ Pictures The Shape Of A Field Surrounding A Current Magnetic Field Inside Current Carrying Wire Varies With R The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. the magnetic field inside a conductor with. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.slideserve.com
PPT ELECTRODYNAMICS PowerPoint Presentation ID162570 Magnetic Field Inside Current Carrying Wire Varies With R (b) this cutaway shows the magnetic field generated by the current in the solenoid. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? The magnetic field should still go in circular. B = μ0 ∙ itot 2π ∙ r2 ∙ r. to find the magnetic field at. Magnetic Field Inside Current Carrying Wire Varies With R.
From mungfali.com
Field Around Current Carrying Wire Magnetic Field Inside Current Carrying Wire Varies With R The magnetic field should still go in circular. B = μ0 ∙ itot 2π ∙ r2 ∙ r. to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. (b) this cutaway shows the magnetic field generated by the current in the solenoid. the strength of the magnetic field created. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.slideserve.com
PPT Calculating the Field Due to a Current PowerPoint Magnetic Field Inside Current Carrying Wire Varies With R The magnetic field should still go in circular. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r.. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.flexiprep.com
Physics Class 12 NCERT Solutions Chapter 4 Moving Charges and Magnetic Field Inside Current Carrying Wire Varies With R to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. the field outside the coils is nearly zero. (b) this cutaway shows the magnetic field generated by the current in the solenoid. what is the magnetic field due to the current at an arbitrary point p along the. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.toppr.com
The current density vec j inside a long, solid cylindrical wire of Magnetic Field Inside Current Carrying Wire Varies With R to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. let's find the expression for the magnetic field inside a straight long wire. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. The magnetic field should still. Magnetic Field Inside Current Carrying Wire Varies With R.
From proper-cooking.info
Field Around A Wire Magnetic Field Inside Current Carrying Wire Varies With R the field outside the coils is nearly zero. to find the magnetic field at a radius r inside the wire, draw a circular loop of radius r. B = μ0 ∙ itot 2π ∙ r2 ∙ r. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law.. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.toppr.com
field B at the centre of a square of side a carrying current I Magnetic Field Inside Current Carrying Wire Varies With R let's find the expression for the magnetic field inside a straight long wire. what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? The magnetic field should still go in circular. B = μ0 ∙ itot 2π ∙ r2 ∙ r. The above formula means the magnetic field. Magnetic Field Inside Current Carrying Wire Varies With R.
From serc.carleton.edu
field around a wire carrying current Magnetic Field Inside Current Carrying Wire Varies With R The magnetic field should still go in circular. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. let's find the expression for the magnetic field inside a straight long wire. (b) this cutaway shows the magnetic field generated by the current in the. Magnetic Field Inside Current Carrying Wire Varies With R.
From electronics.stackexchange.com
field strength of wire (BiotSavart Law Magnetic Field Inside Current Carrying Wire Varies With R the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. B = μ0 ∙ itot 2π ∙ r2 ∙ r. the field outside the coils is nearly zero. the magnetic field inside a conductor with uniform current density j = i/πr 2 can. Magnetic Field Inside Current Carrying Wire Varies With R.
From brainly.in
Which diagram shows the field lines around a current carrying Magnetic Field Inside Current Carrying Wire Varies With R let's find the expression for the magnetic field inside a straight long wire. (b) this cutaway shows the magnetic field generated by the current in the solenoid. the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. to find the magnetic field at. Magnetic Field Inside Current Carrying Wire Varies With R.
From electronics.stackexchange.com
Why is the field inside a coaxial cable the same as it would Magnetic Field Inside Current Carrying Wire Varies With R the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. B = μ0 ∙ itot 2π ∙ r2 ∙ r. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. to find the. Magnetic Field Inside Current Carrying Wire Varies With R.
From pressbooks.bccampus.ca
7.0 Fields Produced by Currents Ampere’s Law Douglas Magnetic Field Inside Current Carrying Wire Varies With R B = μ0 ∙ itot 2π ∙ r2 ∙ r. let's find the expression for the magnetic field inside a straight long wire. The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. to find the magnetic field at a radius. Magnetic Field Inside Current Carrying Wire Varies With R.
From www.youtube.com
Force between two parallel currentcarrying wires YouTube Magnetic Field Inside Current Carrying Wire Varies With R what is the magnetic field due to the current at an arbitrary point p along the axis of the loop? B = μ0 ∙ itot 2π ∙ r2 ∙ r. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. the field outside the coils is nearly. Magnetic Field Inside Current Carrying Wire Varies With R.
From physics.stackexchange.com
Does the Internal field inside of a current Magnetic Field Inside Current Carrying Wire Varies With R The above formula means the magnetic field is zero at centre of cross section of the wire and it has a maximum value for r = r. B = μ0 ∙ itot 2π ∙ r2 ∙ r. the field outside the coils is nearly zero. the magnetic field inside a conductor with uniform current density j = i/πr. Magnetic Field Inside Current Carrying Wire Varies With R.
From physics.stackexchange.com
Field Direction a single one on a Magnetic Field Inside Current Carrying Wire Varies With R the strength of the magnetic field created by current in a long straight wire is given by \[b = \frac{\mu_{0}i}{2 \pi r} \left(long \quad. the magnetic field inside a conductor with uniform current density j = i/πr 2 can be found with ampere's law. B = μ0 ∙ itot 2π ∙ r2 ∙ r. The above formula means. Magnetic Field Inside Current Carrying Wire Varies With R.