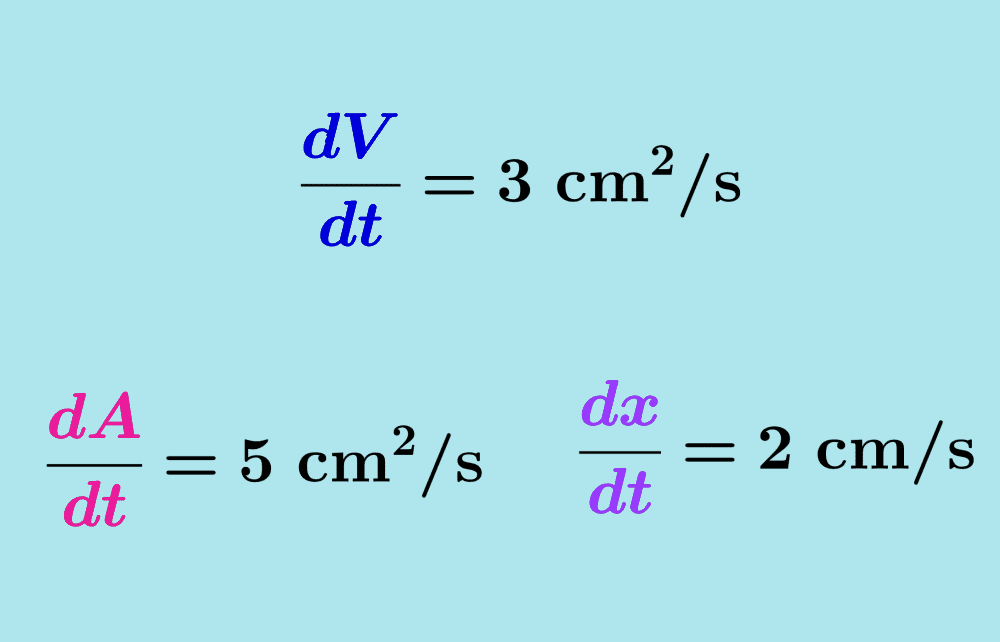Differential Equations Rate Of Change . The diagram above shows a cylindrical water tank. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. In particular we will look at mixing problems (modeling the amount of a. Water is flowing into the tank at a. Apply rates of change to displacement,. In this chapter, we introduce the concept of differential equations. Equations involving derivatives (ie rates of. In this section we will use first order differential equations to model physical situations. A differential equation is an equation that provides a description of a function's derivative, which means that it. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation.
from en.neurochispas.com
A differential equation is an equation for an unknown function that involves the derivative of the unknown function. The diagram above shows a cylindrical water tank. In this section we will use first order differential equations to model physical situations. A differential equation is an equation that provides a description of a function's derivative, which means that it. Equations involving derivatives (ie rates of. In particular we will look at mixing problems (modeling the amount of a. Apply rates of change to displacement,. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. In this chapter, we introduce the concept of differential equations.
Rate of Change with Derivatives Examples and Practice Neurochispas
Differential Equations Rate Of Change Apply rates of change to displacement,. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. In particular we will look at mixing problems (modeling the amount of a. Apply rates of change to displacement,. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. Water is flowing into the tank at a. The diagram above shows a cylindrical water tank. In this section we will use first order differential equations to model physical situations. A differential equation is an equation that provides a description of a function's derivative, which means that it. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. In this chapter, we introduce the concept of differential equations. Equations involving derivatives (ie rates of.
From www.linstitute.net
AQA A Level Maths Pure复习笔记7.4.3 Connected Rates of Change翰林国际教育 Differential Equations Rate Of Change In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. Apply rates of change to displacement,. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. Equations involving derivatives (ie rates of. In particular we will look at mixing problems. Differential Equations Rate Of Change.
From jmzobitz.github.io
Chapter 1 Models of Rates with Data Exploring Modeling with Data and Differential Equations Rate Of Change The diagram above shows a cylindrical water tank. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. Apply rates of change to displacement,. In this chapter, we introduce the concept of differential equations. A differential equation is an equation that provides a description of a function's. Differential Equations Rate Of Change.
From mathsux.org
Rate of Change Algebra Math Lessons Differential Equations Rate Of Change Calculate the average rate of change and explain how it differs from the instantaneous rate of change. Equations involving derivatives (ie rates of. In particular we will look at mixing problems (modeling the amount of a. Apply rates of change to displacement,. Water is flowing into the tank at a. A differential equation is an equation that provides a description. Differential Equations Rate Of Change.
From www.chegg.com
Solved Write a differential equation that fits the physical Differential Equations Rate Of Change In this section we will use first order differential equations to model physical situations. A differential equation is an equation that provides a description of a function's derivative, which means that it. Equations involving derivatives (ie rates of. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. Water is flowing into. Differential Equations Rate Of Change.
From www.youtube.com
Math 121 Relative Rate of Change with Calculus YouTube Differential Equations Rate Of Change In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. Apply rates of change to displacement,. In particular we will look at mixing problems (modeling the amount of a. A differential equation is an equation for an unknown function that involves the derivative of the unknown function.. Differential Equations Rate Of Change.
From mathsathome.com
How to Find the Average Rate of Change Differential Equations Rate Of Change Equations involving derivatives (ie rates of. Water is flowing into the tank at a. In particular we will look at mixing problems (modeling the amount of a. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. A differential equation is an equation that provides a description. Differential Equations Rate Of Change.
From www.ck12.org
Rate of Change Example 1 ( Video ) Algebra CK12 Foundation Differential Equations Rate Of Change A differential equation is an equation for an unknown function that involves the derivative of the unknown function. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. In this chapter, we introduce the concept of differential equations. Apply rates of change to displacement,. A differential equation. Differential Equations Rate Of Change.
From study.com
How to Find the Rate of Change Given a Graph of a Linear Function Differential Equations Rate Of Change Equations involving derivatives (ie rates of. Apply rates of change to displacement,. In particular we will look at mixing problems (modeling the amount of a. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. The diagram above shows a cylindrical water tank. Water is flowing into. Differential Equations Rate Of Change.
From calcworkshop.com
Average Rate Of Change In Calculus (w/ StepbyStep Examples!) Differential Equations Rate Of Change A differential equation is an equation that provides a description of a function's derivative, which means that it. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. In situations involving more than two variables. Differential Equations Rate Of Change.
From www.youtube.com
How to find the average rate of change from a formula Functions Differential Equations Rate Of Change A differential equation is an equation that provides a description of a function's derivative, which means that it. The diagram above shows a cylindrical water tank. In this section we will use first order differential equations to model physical situations. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. Equations involving. Differential Equations Rate Of Change.
From www.youtube.com
Average Rate of Change & the Derivative YouTube Differential Equations Rate Of Change In this chapter, we introduce the concept of differential equations. In particular we will look at mixing problems (modeling the amount of a. In this section we will use first order differential equations to model physical situations. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation.. Differential Equations Rate Of Change.
From www.youtube.com
Linear Equations Slopes and Rates of Change YouTube Differential Equations Rate Of Change Apply rates of change to displacement,. The diagram above shows a cylindrical water tank. A differential equation is an equation that provides a description of a function's derivative, which means that it. Water is flowing into the tank at a. Equations involving derivatives (ie rates of. A differential equation is an equation for an unknown function that involves the derivative. Differential Equations Rate Of Change.
From pathtogrow.com
What is the Rate Of Change Formula A Comprehensive Guide Differential Equations Rate Of Change Equations involving derivatives (ie rates of. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. A differential equation is an equation that provides a description of a function's. Differential Equations Rate Of Change.
From iitutor.com
SACE S2 Specialist Maths, Rates of Change & Differential Equ Differential Equations Rate Of Change Equations involving derivatives (ie rates of. In this section we will use first order differential equations to model physical situations. Water is flowing into the tank at a. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. Calculate the average rate of change and explain how. Differential Equations Rate Of Change.
From mathsathome.com
How to Find the Average Rate of Change Differential Equations Rate Of Change Equations involving derivatives (ie rates of. Water is flowing into the tank at a. In this chapter, we introduce the concept of differential equations. Apply rates of change to displacement,. In particular we will look at mixing problems (modeling the amount of a. In this section we will use first order differential equations to model physical situations. A differential equation. Differential Equations Rate Of Change.
From api-project-1022638073839.appspot.com
Rates of Change Algebra Socratic Differential Equations Rate Of Change In this chapter, we introduce the concept of differential equations. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. Water is flowing into the tank at a. In particular we will look at mixing problems (modeling the amount of a. A differential equation is an equation. Differential Equations Rate Of Change.
From www.coursehero.com
[Solved] Think about a differential equation as a rate of change Differential Equations Rate Of Change In this chapter, we introduce the concept of differential equations. A differential equation is an equation that provides a description of a function's derivative, which means that it. Equations involving derivatives (ie rates of. In particular we will look at mixing problems (modeling the amount of a. Water is flowing into the tank at a. Calculate the average rate of. Differential Equations Rate Of Change.
From www.youtube.com
Concept to Find Function from Rate of Change Antiderivatives for Differential Equations Rate Of Change Water is flowing into the tank at a. Apply rates of change to displacement,. A differential equation is an equation that provides a description of a function's derivative, which means that it. The diagram above shows a cylindrical water tank. Equations involving derivatives (ie rates of. In this section we will use first order differential equations to model physical situations.. Differential Equations Rate Of Change.
From www.youtube.com
Add Math Differentiation Introduction of rate of change YouTube Differential Equations Rate Of Change In this chapter, we introduce the concept of differential equations. A differential equation is an equation that provides a description of a function's derivative, which means that it. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. Equations involving derivatives (ie rates of. The diagram above. Differential Equations Rate Of Change.
From www.youtube.com
IB Rate of Change Differential Calculus Optimisation YouTube Differential Equations Rate Of Change Calculate the average rate of change and explain how it differs from the instantaneous rate of change. In this chapter, we introduce the concept of differential equations. In particular we will look at mixing problems (modeling the amount of a. The diagram above shows a cylindrical water tank. In this section we will use first order differential equations to model. Differential Equations Rate Of Change.
From www.pinterest.nz
How to Solve Differential Equations wikiHow Matemática, Equações Differential Equations Rate Of Change In this section we will use first order differential equations to model physical situations. Apply rates of change to displacement,. In this chapter, we introduce the concept of differential equations. In particular we will look at mixing problems (modeling the amount of a. The diagram above shows a cylindrical water tank. Equations involving derivatives (ie rates of. In situations involving. Differential Equations Rate Of Change.
From www.youtube.com
Changing Harvest Rate Differential Equations in Action YouTube Differential Equations Rate Of Change The diagram above shows a cylindrical water tank. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. A differential equation is an equation that provides a description of a function's derivative, which means that it. Equations involving derivatives (ie rates of. A differential equation is an. Differential Equations Rate Of Change.
From www.cuemath.com
Average Rate of Change Formula Learn Formula for Calculating the Differential Equations Rate Of Change Water is flowing into the tank at a. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. In particular we will look at mixing problems (modeling the amount of a. Apply rates of change. Differential Equations Rate Of Change.
From www.slideserve.com
PPT 2.4 Rates of change and tangent lines PowerPoint Presentation Differential Equations Rate Of Change Equations involving derivatives (ie rates of. In this section we will use first order differential equations to model physical situations. In particular we will look at mixing problems (modeling the amount of a. The diagram above shows a cylindrical water tank. In situations involving more than two variables you can use the chain rule to connect multiple rates of change. Differential Equations Rate Of Change.
From www.ck12.org
Rate of Change Overview ( Video ) Algebra CK12 Foundation Differential Equations Rate Of Change Calculate the average rate of change and explain how it differs from the instantaneous rate of change. The diagram above shows a cylindrical water tank. Apply rates of change to displacement,. A differential equation is an equation that provides a description of a function's derivative, which means that it. In this section we will use first order differential equations to. Differential Equations Rate Of Change.
From www.youtube.com
Differential Equations How to determine the value of the Rate of Differential Equations Rate Of Change The diagram above shows a cylindrical water tank. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. Water is flowing into the tank at a. In this chapter, we introduce the concept of differential. Differential Equations Rate Of Change.
From www.alevelh2maths.com
Differentiation Application Rate of Change ALevel H2 Maths Differential Equations Rate Of Change The diagram above shows a cylindrical water tank. In particular we will look at mixing problems (modeling the amount of a. Equations involving derivatives (ie rates of. Apply rates of change to displacement,. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. In this section we will use first order differential. Differential Equations Rate Of Change.
From www.expii.com
Rate of Change Definition & Example Expii Differential Equations Rate Of Change In particular we will look at mixing problems (modeling the amount of a. Apply rates of change to displacement,. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. In this section we will use first order differential equations to model physical situations. In situations involving more than two variables you can use. Differential Equations Rate Of Change.
From en.neurochispas.com
Rate of Change with Derivatives Examples and Practice Neurochispas Differential Equations Rate Of Change In this chapter, we introduce the concept of differential equations. The diagram above shows a cylindrical water tank. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. Apply. Differential Equations Rate Of Change.
From www.youtube.com
SE Chap 8 Differential Rate Equation YouTube Differential Equations Rate Of Change Calculate the average rate of change and explain how it differs from the instantaneous rate of change. In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation. The diagram above shows a cylindrical water tank. A differential equation is an equation that provides a description of a. Differential Equations Rate Of Change.
From www.coursehero.com
[Solved] The relative rate of change of a differentiable function y = f Differential Equations Rate Of Change A differential equation is an equation for an unknown function that involves the derivative of the unknown function. The diagram above shows a cylindrical water tank. In this section we will use first order differential equations to model physical situations. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. In particular we. Differential Equations Rate Of Change.
From www.slideserve.com
PPT Differential Equations PowerPoint Presentation, free download Differential Equations Rate Of Change Calculate the average rate of change and explain how it differs from the instantaneous rate of change. In this section we will use first order differential equations to model physical situations. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. Water is flowing into the tank at a. Equations involving derivatives. Differential Equations Rate Of Change.
From mathsathome.com
How to Find the Average Rate of Change Differential Equations Rate Of Change Apply rates of change to displacement,. Water is flowing into the tank at a. In this chapter, we introduce the concept of differential equations. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. Equations involving derivatives (ie rates of. A differential equation is an equation that provides a description of a. Differential Equations Rate Of Change.
From mathsathome.com
How to Find the Average Rate of Change Differential Equations Rate Of Change A differential equation is an equation for an unknown function that involves the derivative of the unknown function. The diagram above shows a cylindrical water tank. Apply rates of change to displacement,. Calculate the average rate of change and explain how it differs from the instantaneous rate of change. A differential equation is an equation that provides a description of. Differential Equations Rate Of Change.
From www.youtube.com
Differentiation Connected Rates of Change Example 1 ExamSolutions Differential Equations Rate Of Change Calculate the average rate of change and explain how it differs from the instantaneous rate of change. A differential equation is an equation for an unknown function that involves the derivative of the unknown function. In this section we will use first order differential equations to model physical situations. Apply rates of change to displacement,. Water is flowing into the. Differential Equations Rate Of Change.