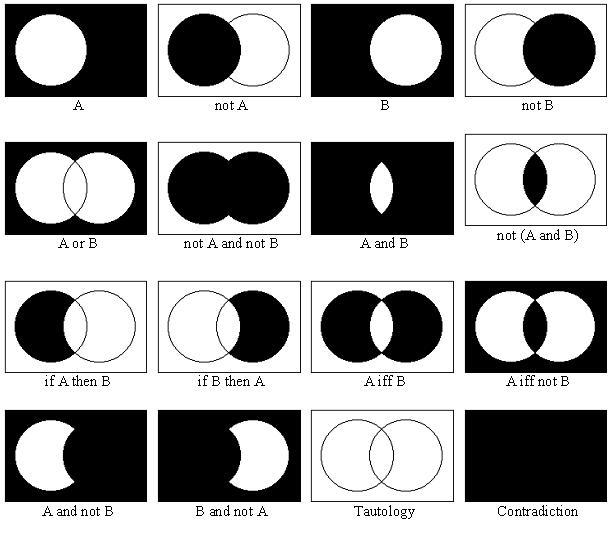
What Is A Bar In Set Theory . $$\bar{b} = b^c = b' = \{x \mid. set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. set is a collection of objects, called its elements. $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. The table below depicts such relationship symbols, along with their meanings and examples: similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. We can list each element (or member) of a set inside curly. guide to ∈ and ⊆. 35 rows a set is a collection of things, usually numbers. In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. We write x 2 a to mean that x is an element of a set a, we also say that x.
from paperpandao1o.blogspot.com
set is a collection of objects, called its elements. set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. $$\bar{b} = b^c = b' = \{x \mid. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. The table below depicts such relationship symbols, along with their meanings and examples: We can list each element (or member) of a set inside curly. guide to ∈ and ⊆. similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. 35 rows a set is a collection of things, usually numbers.
Set Theory
What Is A Bar In Set Theory 35 rows a set is a collection of things, usually numbers. $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. We can list each element (or member) of a set inside curly. set is a collection of objects, called its elements. $$\bar{b} = b^c = b' = \{x \mid. We write x 2 a to mean that x is an element of a set a, we also say that x. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. guide to ∈ and ⊆. 35 rows a set is a collection of things, usually numbers. similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. The table below depicts such relationship symbols, along with their meanings and examples:
From paperpandao1o.blogspot.com
Set Theory What Is A Bar In Set Theory guide to ∈ and ⊆. $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. set theory symbols are used to identify a specific set as well as to determine/show. What Is A Bar In Set Theory.
From notebahadur.com
SET THEORY (Defination,Venn diagram,formuls) NOTE BAHADUR What Is A Bar In Set Theory We can list each element (or member) of a set inside curly. similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. guide to ∈ and ⊆. In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. $i$ is. What Is A Bar In Set Theory.
From sirhunte.teachable.com
SECTION 3 SET THEORY Mr Hunte's Mathematics Academy What Is A Bar In Set Theory In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. $$\bar{b} = b^c = b' = \{x \mid. We can list each element (or member) of a set inside curly. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. guide to ∈ and ⊆. 35. What Is A Bar In Set Theory.
From www.cuemath.com
Sets Definition, Symbols, Examples Set Theory What Is A Bar In Set Theory The table below depicts such relationship symbols, along with their meanings and examples: the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set. What Is A Bar In Set Theory.
From exoqqckld.blob.core.windows.net
What Does 2 Sets Mean at Frank Clemons blog What Is A Bar In Set Theory $$\bar{b} = b^c = b' = \{x \mid. set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. $i$. What Is A Bar In Set Theory.
From www.youtube.com
Partitions of a Set Set Theory YouTube What Is A Bar In Set Theory set is a collection of objects, called its elements. similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. The table below depicts such relationship symbols, along with. What Is A Bar In Set Theory.
From leverageedu.com
Set Theory Formulas, Questions & Referance Books Leverage Edu What Is A Bar In Set Theory similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. We can list each element (or member) of a set inside curly. guide to ∈ and ⊆. In. What Is A Bar In Set Theory.
From www.youtube.com
Set Theory Part 4 Set Difference and Symmetric Difference YouTube What Is A Bar In Set Theory In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. We write x 2 a to mean that x is an element of a set a, we also say that x. The table below depicts such relationship symbols, along with their meanings and examples: similar to other fields in mathematics, set. What Is A Bar In Set Theory.
From math.stackexchange.com
correct Set theory notations. Mathematics Stack Exchange What Is A Bar In Set Theory 35 rows a set is a collection of things, usually numbers. The table below depicts such relationship symbols, along with their meanings and examples: $$\bar{b} = b^c = b' = \{x \mid. We write x 2 a to mean that x is an element of a set a, we also say that x. similar to other fields in. What Is A Bar In Set Theory.
From exoqqckld.blob.core.windows.net
What Does 2 Sets Mean at Frank Clemons blog What Is A Bar In Set Theory guide to ∈ and ⊆. similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. 35 rows a set is a collection of things, usually numbers. The table below depicts such relationship symbols, along with their meanings and examples: set theory symbols are used to identify. What Is A Bar In Set Theory.
From www.slideshare.net
Set theory and relation What Is A Bar In Set Theory set is a collection of objects, called its elements. $$\bar{b} = b^c = b' = \{x \mid. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. 35 rows a set is a collection of things, usually numbers. We can list each element (or member) of a set inside curly. set theory symbols. What Is A Bar In Set Theory.
From www.slideserve.com
PPT Chapter 9 Morphological Image Processing (Digital Image What Is A Bar In Set Theory $$\bar{b} = b^c = b' = \{x \mid. set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. In our first lecture on sets and set theory, we introduced a bunch of new symbols. What Is A Bar In Set Theory.
From www.youtube.com
Set Theory Example Combining Operations YouTube What Is A Bar In Set Theory We can list each element (or member) of a set inside curly. The table below depicts such relationship symbols, along with their meanings and examples: $$\bar{b} = b^c = b' = \{x \mid. We write x 2 a to mean that x is an element of a set a, we also say that x. set is a collection of. What Is A Bar In Set Theory.
From cbselibrary.com
What are the Types of Relations in Set Theory CBSE Library What Is A Bar In Set Theory set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. similar to other fields in mathematics, set theory often. What Is A Bar In Set Theory.
From www.youtube.com
Set Theory Example Union YouTube What Is A Bar In Set Theory similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. guide to ∈ and ⊆. We can list each element (or member) of a set inside curly. $i$ is some set used for. What Is A Bar In Set Theory.
From www.slideserve.com
PPT Basics of Set Theory PowerPoint Presentation, free download ID What Is A Bar In Set Theory 35 rows a set is a collection of things, usually numbers. guide to ∈ and ⊆. similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. We can list each element (or member) of a set inside curly. The table below depicts such relationship symbols, along with. What Is A Bar In Set Theory.
From www.youtube.com
Sets Formulas Set Theory Formula Sets Set Theory Formula of What Is A Bar In Set Theory set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. We can list each element (or member) of a set inside curly. guide to ∈ and ⊆. $i$ is some set used. What Is A Bar In Set Theory.
From thirdspacelearning.com
Set Notation GCSE Maths Steps, Examples & Worksheet What Is A Bar In Set Theory set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. guide to ∈ and ⊆. We can list each element (or member) of a set inside curly. The table below depicts such relationship. What Is A Bar In Set Theory.
From www.youtube.com
SET THEORY Math Animation YouTube What Is A Bar In Set Theory We write x 2 a to mean that x is an element of a set a, we also say that x. $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. set is a collection. What Is A Bar In Set Theory.
From www.youtube.com
Set Theory Types of Sets, Unions and Intersections YouTube What Is A Bar In Set Theory In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. the complement of the set. What Is A Bar In Set Theory.
From www.slideserve.com
PPT Set Theory PowerPoint Presentation, free download ID2398274 What Is A Bar In Set Theory We write x 2 a to mean that x is an element of a set a, we also say that x. $$\bar{b} = b^c = b' = \{x \mid. The table below depicts such relationship symbols, along with their meanings and examples: We can list each element (or member) of a set inside curly. the complement of the set. What Is A Bar In Set Theory.
From onlinemathcenter.com
Math Symbols and Their Meanings Set Theory OMC Math Blog What Is A Bar In Set Theory We write x 2 a to mean that x is an element of a set a, we also say that x. $$\bar{b} = b^c = b' = \{x \mid. guide to ∈ and ⊆. The table below depicts such relationship symbols, along with their meanings and examples: In our first lecture on sets and set theory, we introduced a. What Is A Bar In Set Theory.
From tinytram.com
TinyTram Math Set Theory What Is A Bar In Set Theory We can list each element (or member) of a set inside curly. guide to ∈ and ⊆. 35 rows a set is a collection of things, usually numbers. set is a collection of objects, called its elements. similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to. What Is A Bar In Set Theory.
From www.youtube.com
Introduction to Functions. Set Theory Notation. Examples. Abstract What Is A Bar In Set Theory In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. $$\bar{b} = b^c = b' = \{x \mid. $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. set theory symbols are used to identify a specific set as well as. What Is A Bar In Set Theory.
From www.slideshare.net
Set Theory What Is A Bar In Set Theory The table below depicts such relationship symbols, along with their meanings and examples: We can list each element (or member) of a set inside curly. $$\bar{b} = b^c = b' = \{x \mid. In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. We write x 2 a to mean that x. What Is A Bar In Set Theory.
From www.pinterest.jp
Set Theory Definitions Handout Worksheet Homeschool Discrete What Is A Bar In Set Theory The table below depicts such relationship symbols, along with their meanings and examples: guide to ∈ and ⊆. 35 rows a set is a collection of things, usually numbers. We write x 2 a to mean that x is an element of a set a, we also say that x. $$\bar{b} = b^c = b' = \{x \mid.. What Is A Bar In Set Theory.
From manuallistgelsemine.z13.web.core.windows.net
Venn Diagram Union Of Sets What Is A Bar In Set Theory similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. $$\bar{b} = b^c = b' = \{x \mid. set is a collection of objects, called its elements. 35 rows a set is a collection of things, usually numbers. $i$ is some set used for indexing the. What Is A Bar In Set Theory.
From studylib.net
Set Theory Definitions What Is A Bar In Set Theory set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. guide to ∈ and ⊆. In our first lecture. What Is A Bar In Set Theory.
From fixlibrarycoblasbi.z13.web.core.windows.net
Set Theory Venn Diagram Calculator What Is A Bar In Set Theory set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. We can list each element (or member) of a set inside curly. $$\bar{b} = b^c = b' = \{x \mid. the complement of. What Is A Bar In Set Theory.
From www.geogebra.org
SET TheoryExample 1 (For grade 9) GeoGebra What Is A Bar In Set Theory $$\bar{b} = b^c = b' = \{x \mid. In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. the complement of the set $b$, also commonly denoted as $b'$ or $b^c$. 35 rows a set is a collection of things, usually numbers. set is a collection of objects, called. What Is A Bar In Set Theory.
From www.youtube.com
1. Basics of Set Theory Sets Gate YouTube What Is A Bar In Set Theory guide to ∈ and ⊆. In our first lecture on sets and set theory, we introduced a bunch of new symbols and terminology. The table below depicts such relationship symbols, along with their meanings and examples: 35 rows a set is a collection of things, usually numbers. We can list each element (or member) of a set inside. What Is A Bar In Set Theory.
From www.youtube.com
Set Theory 101 Understanding the Symbols and Notations Important What Is A Bar In Set Theory 35 rows a set is a collection of things, usually numbers. set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. the complement of the set $b$, also commonly denoted as $b'$. What Is A Bar In Set Theory.
From www.youtube.com
Set Theory Proof Example YouTube What Is A Bar In Set Theory set theory symbols are used to identify a specific set as well as to determine/show a relationship between distinct sets or relationships inside a set, such as the relationship between a set and its constituent. similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying. In our first. What Is A Bar In Set Theory.
From studylib.net
Basic Concepts of Set Theory Symbols & Terminology Defining Sets What Is A Bar In Set Theory We write x 2 a to mean that x is an element of a set a, we also say that x. $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer. What Is A Bar In Set Theory.
From thirdspacelearning.com
Set Notation GCSE Maths Steps, Examples & Worksheet What Is A Bar In Set Theory $i$ is some set used for indexing the elements in $m$, which must exist since otherwise the subscript of. We can list each element (or member) of a set inside curly. 35 rows a set is a collection of things, usually numbers. set theory symbols are used to identify a specific set as well as to determine/show. What Is A Bar In Set Theory.