Are Corners Critical Points . However, a function need not have a local extremum at a critical point. Describe how to use critical points to locate absolute extrema over a closed. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not defined. Critical points, also known as stationary points (?), is any point where the derivative is equal to 0. This can be found using the same method as above. A continuous function over a. (corners and cusps make thomas cuss. Let us see how to find the critical points of a function by its. If a function has a local extremum, the point at which it occurs must be a critical point. No train can travel on such. Explain how to find the critical points of a function over a closed interval; In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to.
from www.studocu.com
However, a function need not have a local extremum at a critical point. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not defined. No train can travel on such. A continuous function over a. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. (corners and cusps make thomas cuss. Let us see how to find the critical points of a function by its. If a function has a local extremum, the point at which it occurs must be a critical point. This can be found using the same method as above. Describe how to use critical points to locate absolute extrema over a closed.
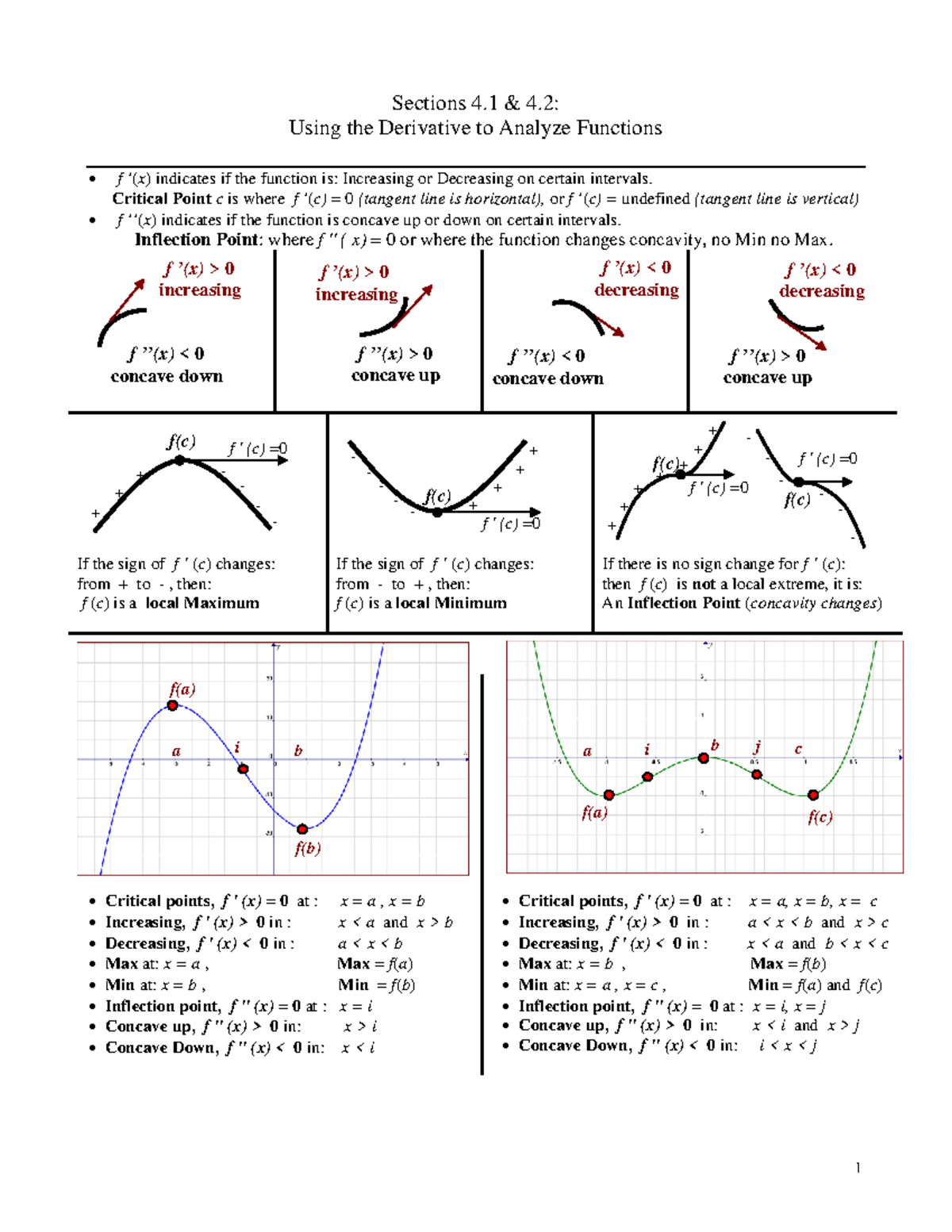
Sec41 Critical and Inflection Points Sections 4 & 4 Using the
Are Corners Critical Points This can be found using the same method as above. If a function has a local extremum, the point at which it occurs must be a critical point. A continuous function over a. Let us see how to find the critical points of a function by its. Describe how to use critical points to locate absolute extrema over a closed. No train can travel on such. (corners and cusps make thomas cuss. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not defined. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. This can be found using the same method as above. However, a function need not have a local extremum at a critical point. Explain how to find the critical points of a function over a closed interval; Critical points, also known as stationary points (?), is any point where the derivative is equal to 0. In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative.
From www.researchgate.net
4 Critical points and curves on a plane (a) the nodal point, (b) the Are Corners Critical Points (corners and cusps make thomas cuss. No train can travel on such. In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative. Let us see how to find the critical points of a function by its. A critical point of a function y = f(x) is a. Are Corners Critical Points.
From www.alamy.com
Red color of corner label banner with word HACCP (Hazard Analysis Are Corners Critical Points In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. If a function has a local extremum, the point at which it occurs must be a critical point. A continuous function over a. However, a function need not have a local extremum at a critical point. Critical points, also known as. Are Corners Critical Points.
From www.slideserve.com
PPT Mastering Mathematical Formulas How to Identify Critical Points Are Corners Critical Points (corners and cusps make thomas cuss. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. Critical points, also known as stationary points (?), is any point where the derivative is equal to 0. In this section we will define critical points for functions of two variables and discuss a method. Are Corners Critical Points.
From studylib.net
CURVE SKETCHING (Critical Points) Are Corners Critical Points Explain how to find the critical points of a function over a closed interval; Critical points, also known as stationary points (?), is any point where the derivative is equal to 0. However, a function need not have a local extremum at a critical point. (corners and cusps make thomas cuss. A critical point of a function y = f(x). Are Corners Critical Points.
From www.slideshare.net
11X1 T09 02 critical points Are Corners Critical Points If a function has a local extremum, the point at which it occurs must be a critical point. However, a function need not have a local extremum at a critical point. In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative. Explain how to find the critical. Are Corners Critical Points.
From articles.outlier.org
Critical Points Your Calculus 101 Guide Outlier Are Corners Critical Points A continuous function over a. In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative. However, a function need not have a local extremum at a critical point. Let us see how to find the critical points of a function by its. Critical points, also known as. Are Corners Critical Points.
From www.studocu.com
Sec41 Critical and Inflection Points Sections 4 & 4 Using the Are Corners Critical Points A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not defined. A continuous function over a. In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative.. Are Corners Critical Points.
From www.coursehero.com
[Solved] 1. Find the critical points, absolute maximum and absolute Are Corners Critical Points No train can travel on such. A continuous function over a. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not defined. However, a function need not have a local extremum at a critical point. Critical points, also known. Are Corners Critical Points.
From www.researchgate.net
Determination of critical points. Boundary points (a), and critical Are Corners Critical Points (corners and cusps make thomas cuss. A continuous function over a. Critical points, also known as stationary points (?), is any point where the derivative is equal to 0. If a function has a local extremum, the point at which it occurs must be a critical point. A critical point of a function y = f(x) is a point (c,. Are Corners Critical Points.
From www.slideshare.net
Critical points Are Corners Critical Points In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not defined. Critical points, also known as stationary points (?), is. Are Corners Critical Points.
From www.youtube.com
Finding Critical Points YouTube Are Corners Critical Points In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not defined. Describe how to use critical. Are Corners Critical Points.
From www.studocu.com
chapter 49 three critical points ATI Nursing Education 3 Critical Are Corners Critical Points However, a function need not have a local extremum at a critical point. Let us see how to find the critical points of a function by its. A continuous function over a. If a function has a local extremum, the point at which it occurs must be a critical point. Explain how to find the critical points of a function. Are Corners Critical Points.
From www.researchgate.net
Critical points of A. Download Scientific Diagram Are Corners Critical Points This can be found using the same method as above. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not. Are Corners Critical Points.
From www.youtube.com
Critical Points from a Graph YouTube Are Corners Critical Points In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. Critical points, also known as stationary points (?), is any point where the derivative is equal to 0. Let us see how to find the critical points of a function by its. If a function has a local extremum, the point. Are Corners Critical Points.
From www.youtube.com
Finding Critical Points YouTube Are Corners Critical Points No train can travel on such. Explain how to find the critical points of a function over a closed interval; Let us see how to find the critical points of a function by its. A continuous function over a. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. In this. Are Corners Critical Points.
From www.showme.com
ShowMe critical points Are Corners Critical Points Let us see how to find the critical points of a function by its. No train can travel on such. (corners and cusps make thomas cuss. If a function has a local extremum, the point at which it occurs must be a critical point. Describe how to use critical points to locate absolute extrema over a closed. A continuous function. Are Corners Critical Points.
From www.slideshare.net
11X1 T09 02 critical points Are Corners Critical Points (corners and cusps make thomas cuss. If a function has a local extremum, the point at which it occurs must be a critical point. In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative. A critical point of a function y = f(x) is a point (c,. Are Corners Critical Points.
From math.stackexchange.com
real analysis Reconstructing a function from its critical points and Are Corners Critical Points (corners and cusps make thomas cuss. If a function has a local extremum, the point at which it occurs must be a critical point. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. Critical points, also known as stationary points (?), is any point where the derivative is equal to. Are Corners Critical Points.
From jbacamath.weebly.com
AP Calculus AB Are Corners Critical Points A continuous function over a. Let us see how to find the critical points of a function by its. This can be found using the same method as above. However, a function need not have a local extremum at a critical point. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key. Are Corners Critical Points.
From www.sdpuo.com
The Complete Guide to Finding Critical Points in Calculus Definitions Are Corners Critical Points In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative. No train can travel on such. This can be found using the same method as above. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. (corners and. Are Corners Critical Points.
From www.youtube.com
Finding critical points where undefined YouTube Are Corners Critical Points Explain how to find the critical points of a function over a closed interval; If a function has a local extremum, the point at which it occurs must be a critical point. Let us see how to find the critical points of a function by its. A continuous function over a. A critical point of a function y = f(x). Are Corners Critical Points.
From www.jirka.org
Stability and classification of isolated critical points Are Corners Critical Points A continuous function over a. Let us see how to find the critical points of a function by its. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either. Are Corners Critical Points.
From www.numerade.com
SOLVEDFind all critical points. Indicate whether each such point gives Are Corners Critical Points (corners and cusps make thomas cuss. Describe how to use critical points to locate absolute extrema over a closed. Let us see how to find the critical points of a function by its. However, a function need not have a local extremum at a critical point. In this section we will define critical points for functions of two variables and. Are Corners Critical Points.
From www.youtube.com
Section 4.1 Finding Critical Points from a Graph YouTube Are Corners Critical Points This can be found using the same method as above. However, a function need not have a local extremum at a critical point. Describe how to use critical points to locate absolute extrema over a closed. In this section we will define critical points for functions of two variables and discuss a method for determining if they are relative. No. Are Corners Critical Points.
From www.studocu.com
Critical Points 1 practice math homework CRITICAL POINTS PART 1 Are Corners Critical Points This can be found using the same method as above. No train can travel on such. If a function has a local extremum, the point at which it occurs must be a critical point. Let us see how to find the critical points of a function by its. A critical point of a function y = f(x) is a point. Are Corners Critical Points.
From courses.lumenlearning.com
Extrema and Critical Points Calculus I Are Corners Critical Points No train can travel on such. If a function has a local extremum, the point at which it occurs must be a critical point. This can be found using the same method as above. Let us see how to find the critical points of a function by its. In this section we will define critical points for functions of two. Are Corners Critical Points.
From www.youtube.com
Learn Calculus The Three Types of Critical Points YouTube Are Corners Critical Points If a function has a local extremum, the point at which it occurs must be a critical point. Critical points, also known as stationary points (?), is any point where the derivative is equal to 0. In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. In this section we will. Are Corners Critical Points.
From thinkingpathwayz.weebly.com
Compass Points THINKING PATHWAYS Are Corners Critical Points (corners and cusps make thomas cuss. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not defined. This can be found using the same method as above. A continuous function over a. Describe how to use critical points to. Are Corners Critical Points.
From docslib.org
What Is a Corner Point? • How Should We Define Corner Points? • Under Are Corners Critical Points This can be found using the same method as above. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either the derivative is 0 (or) the derivative is not defined. If a function has a local extremum, the point at which it occurs must be a critical point.. Are Corners Critical Points.
From www.youtube.com
What are Critical Points ?? YouTube Are Corners Critical Points This can be found using the same method as above. A continuous function over a. However, a function need not have a local extremum at a critical point. No train can travel on such. Describe how to use critical points to locate absolute extrema over a closed. In many cases, corner points represent the boundaries of feasible regions in constrained. Are Corners Critical Points.
From www.researchgate.net
The critical point ωt = π/4. Download Scientific Diagram Are Corners Critical Points (corners and cusps make thomas cuss. This can be found using the same method as above. Explain how to find the critical points of a function over a closed interval; Let us see how to find the critical points of a function by its. If a function has a local extremum, the point at which it occurs must be a. Are Corners Critical Points.
From hartleymath.com
HartleyMath Maxima and Minima Are Corners Critical Points No train can travel on such. A continuous function over a. However, a function need not have a local extremum at a critical point. This can be found using the same method as above. Explain how to find the critical points of a function over a closed interval; (corners and cusps make thomas cuss. In many cases, corner points represent. Are Corners Critical Points.
From www.chegg.com
Solved Find the critical point(s) and classify them as local Are Corners Critical Points A continuous function over a. Let us see how to find the critical points of a function by its. This can be found using the same method as above. (corners and cusps make thomas cuss. Describe how to use critical points to locate absolute extrema over a closed. A critical point of a function y = f(x) is a point. Are Corners Critical Points.
From socratic.org
How are critical points related to local and absolute extrema? Socratic Are Corners Critical Points In many cases, corner points represent the boundaries of feasible regions in constrained optimization scenarios, making them key to. (corners and cusps make thomas cuss. However, a function need not have a local extremum at a critical point. A critical point of a function y = f(x) is a point (c, f(c)) on the graph of f(x) at which either. Are Corners Critical Points.
From www.slideserve.com
PPT How should we define corner points? PowerPoint Presentation, free Are Corners Critical Points Describe how to use critical points to locate absolute extrema over a closed. A continuous function over a. Critical points, also known as stationary points (?), is any point where the derivative is equal to 0. This can be found using the same method as above. In many cases, corner points represent the boundaries of feasible regions in constrained optimization. Are Corners Critical Points.