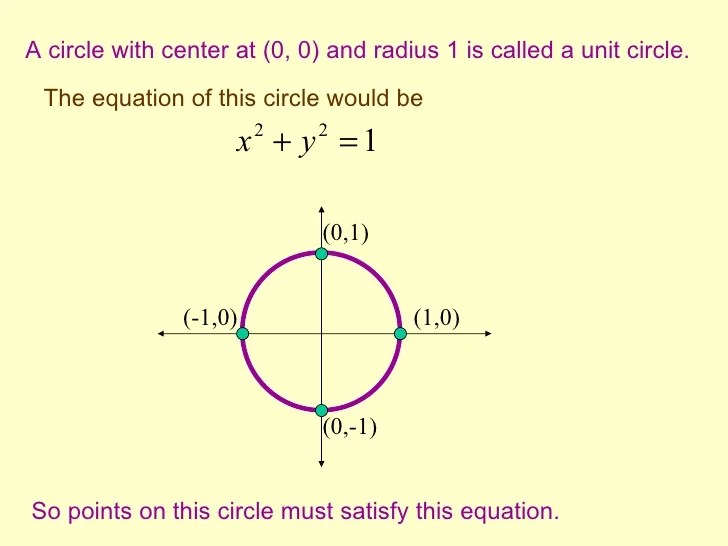
Circular Function Value . The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. Derivatives of sin x and cos x. As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. What are the values of the six circular functions of q? The logic of radian measure; The other four functions are derived using. Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. The values of the sine and cosine follow from the definitions and are the coordinates of point p. This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. It is worth taking the time to memorize the tangent and cotangent values of the common angles summarized below.
from www.slideshare.net
This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). The other four functions are derived using. It is worth taking the time to memorize the tangent and cotangent values of the common angles summarized below. Derivatives of sin x and cos x. Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. What are the values of the six circular functions of q? Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. The logic of radian measure;
Circular functions
Circular Function Value Derivatives of sin x and cos x. The other four functions are derived using. Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. It is worth taking the time to memorize the tangent and cotangent values of the common angles summarized below. The logic of radian measure; The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. What are the values of the six circular functions of q? Derivatives of sin x and cos x. The values of the sine and cosine follow from the definitions and are the coordinates of point p. As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles.
From educationalsitevd.wordpress.com
How to find the exact values of the six circular function Circular Function Value The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. The other four functions are derived using. The logic of radian measure; What are the values of the six circular functions of q? It is worth taking the time to memorize the tangent and cotangent. Circular Function Value.
From www.chegg.com
Solved The figure shows an angle θ in standard position with Circular Function Value This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. Derivatives of sin x and cos x. The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. The values. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value The values of the sine and cosine follow from the definitions and are the coordinates of point p. The logic of radian measure; Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. The other four functions are derived using. Derivatives of sin x and cos x. Coupling theorem 10.6 with. Circular Function Value.
From www.slideserve.com
PPT 3.3 Definition III Circular Functions PowerPoint Presentation Circular Function Value The other four functions are derived using. Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. Derivatives of sin x and cos x. The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. What are. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value The other four functions are derived using. This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. What are the values of the six circular functions of q? The logic of radian measure; It is worth taking the time to memorize the tangent and. Circular Function Value.
From quizlet.com
Find each exact circular function value. \sin \left(\f Quizlet Circular Function Value The other four functions are derived using. It is worth taking the time to memorize the tangent and cotangent values of the common angles summarized below. The logic of radian measure; The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. Coupling theorem 10.6 with. Circular Function Value.
From socratic.org
How to find exact values of circular functions? Socratic Circular Function Value This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. It is worth taking the time to memorize the tangent and cotangent values of the common angles summarized below. What are the values of the six circular functions of q? Again, your teacher may. Circular Function Value.
From www.numerade.com
Find the exact circular function value for each o… Circular Function Value The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. The other four functions are derived using. The values of the sine and cosine follow from the definitions and are the coordinates of point p. Again, your teacher may have demonstrate how you can get. Circular Function Value.
From www.studypool.com
SOLUTION The six circular functions Studypool Circular Function Value The logic of radian measure; The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. The values of the sine and cosine follow from the definitions and are the coordinates of point p. Derivatives of sin x and cos x. The other four functions are. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). What are the values of the six circular functions of q? This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles.. Circular Function Value.
From freevcenotes.com
Circular Functions VCE Methods Circular Function Value This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. The other four functions are derived using. As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). Coupling theorem 10.6 with. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value The values of the sine and cosine follow from the definitions and are the coordinates of point p. Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. It is worth taking the time to memorize the tangent and cotangent values of the common angles summarized below. This is an important observation because it allows us. Circular Function Value.
From freevcenotes.com
Circular Functions VCE Methods Circular Function Value Derivatives of sin x and cos x. The other four functions are derived using. Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. What are the values of the six circular functions of q? This is an important observation because it allows us to define the sine and cosine as. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. What are the values of the six circular functions of q? The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. The other four functions are derived using. As we. Circular Function Value.
From www.youtube.com
GRAPHING CIRCULAR FUNCTIONS (Part 1 Introduction) YouTube Circular Function Value Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. What are the values of the six circular functions of q? As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). This is an important observation because it. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value Derivatives of sin x and cos x. As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. The values of the sine and cosine follow from the definitions and are the coordinates of. Circular Function Value.
From www.geogebra.org
Trigonometric/circular functions GeoGebra Circular Function Value This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. The logic of radian measure; Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. The values of the sine and cosine follow from the. Circular Function Value.
From quizlet.com
Determine thw exact circular function value. \cos \frac Quizlet Circular Function Value What are the values of the six circular functions of q? As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. It. Circular Function Value.
From study.com
Circular Functions Equations & Examples Video & Lesson Transcript Circular Function Value Derivatives of sin x and cos x. The other four functions are derived using. Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). The x and y. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value What are the values of the six circular functions of q? The other four functions are derived using. The values of the sine and cosine follow from the definitions and are the coordinates of point p. Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. The logic of radian measure; Derivatives of sin x and. Circular Function Value.
From www.bartleby.com
Answered Find the exact circular function value.… bartleby Circular Function Value Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead. Circular Function Value.
From www.ck12.org
Circular Functions of Real Numbers CK12 Foundation Circular Function Value Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. The logic of radian measure; It is worth taking the time to memorize the tangent and. Circular Function Value.
From www.youtube.com
Exact Values of Circular Function YouTube Circular Function Value As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. The other four functions are derived using. It is worth taking the time to memorize the tangent and cotangent values of the common. Circular Function Value.
From www.youtube.com
8.2a Part 1 Circular Function Values YouTube Circular Function Value This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles. Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. The other four functions are derived using. Derivatives of sin x and cos x. The logic of radian measure; It. Circular Function Value.
From www.youtube.com
Circular Functions YouTube Circular Function Value Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). What are the values of the six circular functions of q? The values of the sine and cosine. Circular Function Value.
From www.youtube.com
Section 1.5 Finding the Values of the Circular Functions YouTube Circular Function Value What are the values of the six circular functions of q? As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). Derivatives of sin x and cos x. The values of the sine and cosine follow from the definitions and are the coordinates of point p. The. Circular Function Value.
From www.youtube.com
SIX CIRCULAR FUNCTIONS YouTube Circular Function Value Derivatives of sin x and cos x. Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. The x and y coordinates for each point along the circle may be ascertained by reading off the values on. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. This is. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. What are the values of the six circular functions of q? Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) =. Circular Function Value.
From www.slideserve.com
PPT 3.3 Definition III Circular Functions PowerPoint Presentation Circular Function Value Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. The other four functions are derived using. Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. The x and y coordinates for each point along the circle may be ascertained by reading off the values on. Circular Function Value.
From precalculusrubio2022group3.wordpress.com
The Six Circular Functions The Calculus Orienteer A Guide Circular Function Value Coupling theorem 10.6 with the reference angle theorem, theorem 10.2, we get the following. Derivatives of sin x and cos x. It is worth taking the time to memorize the tangent and cotangent values of the common angles summarized below. Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. As. Circular Function Value.
From www.slideshare.net
Circular functions Circular Function Value Again, your teacher may have demonstrate how you can get all of the formulae below form the unit circle. The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. The other four functions are derived using. This is an important observation because it allows us. Circular Function Value.
From quizlet.com
topic 3. circular functions and trigonometry Diagram Quizlet Circular Function Value It is worth taking the time to memorize the tangent and cotangent values of the common angles summarized below. The logic of radian measure; As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). Derivatives of sin x and cos x. What are the values of the. Circular Function Value.
From www.cuemath.com
Unit circle Solved Examples Geometry Cuemath Circular Function Value What are the values of the six circular functions of q? As we saw in section 10.2, we can use the pythagorean identity, cos2(θ) + sin2(θ) = 1, to find cos(θ) by knowing sin(θ). This is an important observation because it allows us to define the sine and cosine as functions of real numbers instead of as functions of angles.. Circular Function Value.