Universal Property Of One Point Compactification . Theorem 2.3 a space has a. To see a part of this, assume y is. In bishop's constructive development of analysis, metric spaces are. Then we have the following universal property: The commutativity $f = \phi \circ g$ forces the definition of $g$: Let x x be a locally compact space, and let i: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Given a topological space x, we wish to construct a compact space y by appending one point:
from hidenori-shinohara.github.io
The commutativity $f = \phi \circ g$ forces the definition of $g$: To see a part of this, assume y is. Given a topological space x, we wish to construct a compact space y by appending one point: Theorem 2.3 a space has a. Then we have the following universal property: Let x x be a locally compact space, and let i: In bishop's constructive development of analysis, metric spaces are. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to.
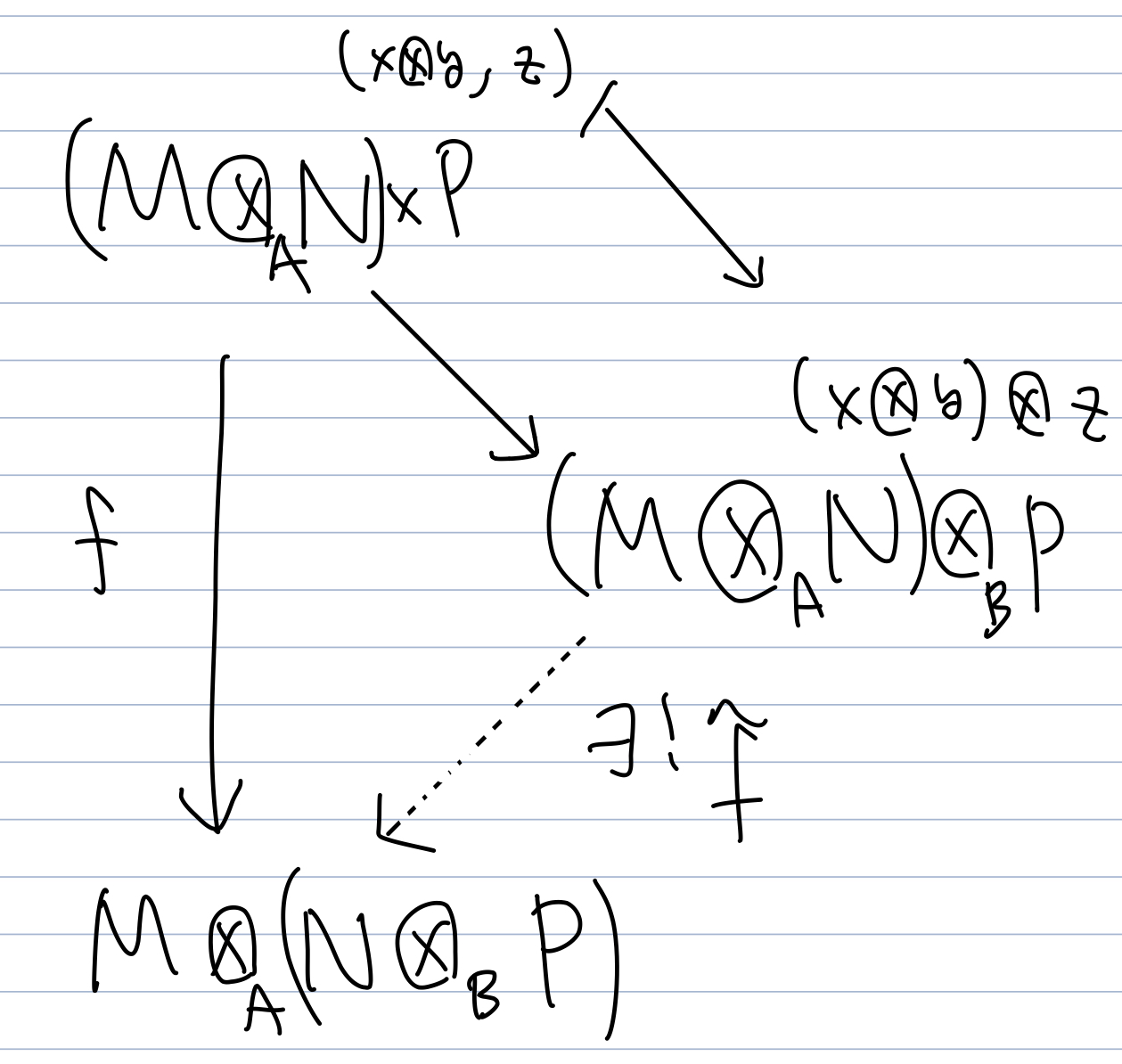
An application of the universal property of a tensor product
Universal Property Of One Point Compactification To see a part of this, assume y is. Let x x be a locally compact space, and let i: Given a topological space x, we wish to construct a compact space y by appending one point: To see a part of this, assume y is. Then we have the following universal property: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Theorem 2.3 a space has a. The commutativity $f = \phi \circ g$ forces the definition of $g$: In bishop's constructive development of analysis, metric spaces are.
From quizizz.com
Properties of Matter Review Quizizz Universal Property Of One Point Compactification Given a topological space x, we wish to construct a compact space y by appending one point: To see a part of this, assume y is. The commutativity $f = \phi \circ g$ forces the definition of $g$: Then we have the following universal property: In bishop's constructive development of analysis, metric spaces are. If $x \in x$, then $g(x). Universal Property Of One Point Compactification.
From studylib.net
Universal Properties of Impure Programming Languages Universal Property Of One Point Compactification In bishop's constructive development of analysis, metric spaces are. Given a topological space x, we wish to construct a compact space y by appending one point: To see a part of this, assume y is. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. The commutativity $f = \phi \circ g$ forces the definition of. Universal Property Of One Point Compactification.
From joirymvgi.blob.core.windows.net
Example Of Universal Solvent In Biology at Thomas Dimauro blog Universal Property Of One Point Compactification To see a part of this, assume y is. Given a topological space x, we wish to construct a compact space y by appending one point: In bishop's constructive development of analysis, metric spaces are. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Let x x be a locally compact space, and let i:. Universal Property Of One Point Compactification.
From upsystems.com.au
Universal Property Systems as your Real Estate Marketing Provider Universal Property Of One Point Compactification In bishop's constructive development of analysis, metric spaces are. Theorem 2.3 a space has a. Let x x be a locally compact space, and let i: To see a part of this, assume y is. Given a topological space x, we wish to construct a compact space y by appending one point: If $x \in x$, then $g(x) \in g[x]$. Universal Property Of One Point Compactification.
From www.youtube.com
Complete Derivation Universal Property of the Tensor Product YouTube Universal Property Of One Point Compactification Let x x be a locally compact space, and let i: Given a topological space x, we wish to construct a compact space y by appending one point: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. The commutativity $f = \phi \circ g$ forces the definition of $g$: To see a part of this,. Universal Property Of One Point Compactification.
From math.stackexchange.com
linear algebra How to prove the uniqueness of the universal property Universal Property Of One Point Compactification To see a part of this, assume y is. In bishop's constructive development of analysis, metric spaces are. Then we have the following universal property: Given a topological space x, we wish to construct a compact space y by appending one point: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Let x x be. Universal Property Of One Point Compactification.
From universalproperty.com
Find An Insurance Agent Universal Property & Casualty Insurance Universal Property Of One Point Compactification Given a topological space x, we wish to construct a compact space y by appending one point: Let x x be a locally compact space, and let i: The commutativity $f = \phi \circ g$ forces the definition of $g$: Theorem 2.3 a space has a. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to.. Universal Property Of One Point Compactification.
From www.mdpi.com
Entropy Free FullText Universal Property of Quantum Gravity Universal Property Of One Point Compactification The commutativity $f = \phi \circ g$ forces the definition of $g$: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. In bishop's constructive development of analysis, metric spaces are. To see a part of this, assume y is. Let x x be a locally compact space, and let i: Given a topological space x,. Universal Property Of One Point Compactification.
From math.stackexchange.com
abstract algebra Construction of Free Module as Adjunction Aluffi Universal Property Of One Point Compactification To see a part of this, assume y is. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Given a topological space x, we wish to construct a compact space y by appending one point: Then we have the following universal property: In bishop's constructive development of analysis, metric spaces are. Theorem 2.3 a space. Universal Property Of One Point Compactification.
From slideplayer.com
dark matter Properties stable nonrelativistic nonbaryonic ppt download Universal Property Of One Point Compactification To see a part of this, assume y is. Given a topological space x, we wish to construct a compact space y by appending one point: Then we have the following universal property: Theorem 2.3 a space has a. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Let x x be a locally compact. Universal Property Of One Point Compactification.
From joiieypbm.blob.core.windows.net
Example Of Solvent Water at Nicholas Matthews blog Universal Property Of One Point Compactification Given a topological space x, we wish to construct a compact space y by appending one point: Let x x be a locally compact space, and let i: Theorem 2.3 a space has a. Then we have the following universal property: In bishop's constructive development of analysis, metric spaces are. The commutativity $f = \phi \circ g$ forces the definition. Universal Property Of One Point Compactification.
From www.cambridge.org
The complexification of a compact group (Chapter 12) Lectures on Lie Universal Property Of One Point Compactification Let x x be a locally compact space, and let i: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Then we have the following universal property: The commutativity $f = \phi \circ g$ forces the definition of $g$: Given a topological space x, we wish to construct a compact space y by appending one. Universal Property Of One Point Compactification.
From www.semanticscholar.org
Figure 1 from Universal intermittent properties of particle Universal Property Of One Point Compactification Then we have the following universal property: In bishop's constructive development of analysis, metric spaces are. To see a part of this, assume y is. The commutativity $f = \phi \circ g$ forces the definition of $g$: Theorem 2.3 a space has a. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Let x x. Universal Property Of One Point Compactification.
From www.scribd.com
The Universal Property of The Quotient PDF Group (Mathematics Universal Property Of One Point Compactification To see a part of this, assume y is. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Given a topological space x, we wish to construct a compact space y by appending one point: Theorem 2.3 a space has a. Let x x be a locally compact space, and let i: The commutativity $f. Universal Property Of One Point Compactification.
From animalia-life.club
Properties Of Water Polarity Universal Property Of One Point Compactification Then we have the following universal property: Theorem 2.3 a space has a. Let x x be a locally compact space, and let i: In bishop's constructive development of analysis, metric spaces are. The commutativity $f = \phi \circ g$ forces the definition of $g$: To see a part of this, assume y is. If $x \in x$, then $g(x). Universal Property Of One Point Compactification.
From studylib.net
Universal Properties of the TwoDimensional KuramotoSivashinsky Universal Property Of One Point Compactification To see a part of this, assume y is. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Let x x be a locally compact space, and let i: In bishop's constructive development of analysis, metric spaces are. Then we have the following universal property: The commutativity $f = \phi \circ g$ forces the definition. Universal Property Of One Point Compactification.
From universal-property.org
Ours The Case for Universal Property Universal Property Of One Point Compactification If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. The commutativity $f = \phi \circ g$ forces the definition of $g$: Theorem 2.3 a space has a. Given a topological space x, we wish to construct a compact space y by appending one point: Then we have the following universal property: Let x x be. Universal Property Of One Point Compactification.
From math.stackexchange.com
abstract algebra Dummit and Foote Universal Property of Tensor Universal Property Of One Point Compactification Theorem 2.3 a space has a. To see a part of this, assume y is. Then we have the following universal property: Let x x be a locally compact space, and let i: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. The commutativity $f = \phi \circ g$ forces the definition of $g$: Given. Universal Property Of One Point Compactification.
From www.researchgate.net
(PDF) Universal properties of boundary and interface charges in Universal Property Of One Point Compactification The commutativity $f = \phi \circ g$ forces the definition of $g$: To see a part of this, assume y is. Let x x be a locally compact space, and let i: Given a topological space x, we wish to construct a compact space y by appending one point: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must. Universal Property Of One Point Compactification.
From universalproperty.com.au
Our Team Universal Property Universal Property Of One Point Compactification Let x x be a locally compact space, and let i: In bishop's constructive development of analysis, metric spaces are. To see a part of this, assume y is. Given a topological space x, we wish to construct a compact space y by appending one point: Then we have the following universal property: If $x \in x$, then $g(x) \in. Universal Property Of One Point Compactification.
From www.mdpi.com
Entropy Free FullText Universal Property of Quantum Gravity Universal Property Of One Point Compactification If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Then we have the following universal property: Given a topological space x, we wish to construct a compact space y by appending one point: In bishop's constructive development of analysis, metric spaces are. To see a part of this, assume y is. The commutativity $f =. Universal Property Of One Point Compactification.
From joirymvgi.blob.core.windows.net
Example Of Universal Solvent In Biology at Thomas Dimauro blog Universal Property Of One Point Compactification The commutativity $f = \phi \circ g$ forces the definition of $g$: Given a topological space x, we wish to construct a compact space y by appending one point: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. To see a part of this, assume y is. Then we have the following universal property: Let. Universal Property Of One Point Compactification.
From www.slideserve.com
PPT 1º THE MOLECULE 2º PHYSICAL PROPERTIES 3º STATES OF WATER 4º THE Universal Property Of One Point Compactification If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. To see a part of this, assume y is. Theorem 2.3 a space has a. Let x x be a locally compact space, and let i: The commutativity $f = \phi \circ g$ forces the definition of $g$: Given a topological space x, we wish to. Universal Property Of One Point Compactification.
From math.stackexchange.com
category theory What is a universal property? Mathematics Stack Universal Property Of One Point Compactification To see a part of this, assume y is. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Then we have the following universal property: Let x x be a locally compact space, and let i: The commutativity $f = \phi \circ g$ forces the definition of $g$: Theorem 2.3 a space has a. Given. Universal Property Of One Point Compactification.
From www.slideserve.com
PPT The Properties of Water PowerPoint Presentation, free download Universal Property Of One Point Compactification To see a part of this, assume y is. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Given a topological space x, we wish to construct a compact space y by appending one point: In bishop's constructive development of analysis, metric spaces are. Theorem 2.3 a space has a. Let x x be a. Universal Property Of One Point Compactification.
From hidenori-shinohara.github.io
An application of the universal property of a tensor product Universal Property Of One Point Compactification In bishop's constructive development of analysis, metric spaces are. The commutativity $f = \phi \circ g$ forces the definition of $g$: Given a topological space x, we wish to construct a compact space y by appending one point: Then we have the following universal property: Let x x be a locally compact space, and let i: Theorem 2.3 a space. Universal Property Of One Point Compactification.
From universalproperty.com
About Us Universal Property & Casualty Insurance Universal Property Of One Point Compactification Given a topological space x, we wish to construct a compact space y by appending one point: In bishop's constructive development of analysis, metric spaces are. Theorem 2.3 a space has a. Let x x be a locally compact space, and let i: The commutativity $f = \phi \circ g$ forces the definition of $g$: Then we have the following. Universal Property Of One Point Compactification.
From www.studocu.com
Universal properties of languageD No one knows just how this Universal Property Of One Point Compactification In bishop's constructive development of analysis, metric spaces are. To see a part of this, assume y is. Then we have the following universal property: Theorem 2.3 a space has a. Given a topological space x, we wish to construct a compact space y by appending one point: If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map. Universal Property Of One Point Compactification.
From www.scribd.com
Universal Properties of Cells PDF Cell (Biology) Metabolism Universal Property Of One Point Compactification Theorem 2.3 a space has a. Given a topological space x, we wish to construct a compact space y by appending one point: Let x x be a locally compact space, and let i: To see a part of this, assume y is. In bishop's constructive development of analysis, metric spaces are. The commutativity $f = \phi \circ g$ forces. Universal Property Of One Point Compactification.
From www.upmanagement.org
Universal Property Management Universal Property Of One Point Compactification If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. Theorem 2.3 a space has a. Then we have the following universal property: Let x x be a locally compact space, and let i: Given a topological space x, we wish to construct a compact space y by appending one point: In bishop's constructive development of. Universal Property Of One Point Compactification.
From www.researchgate.net
(PDF) Internal Direct Products and the Universal Property of Direct Universal Property Of One Point Compactification Let x x be a locally compact space, and let i: To see a part of this, assume y is. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. The commutativity $f = \phi \circ g$ forces the definition of $g$: In bishop's constructive development of analysis, metric spaces are. Given a topological space x,. Universal Property Of One Point Compactification.
From www.linkedin.com
Universal Property & Casualty Insurance Company LinkedIn Universal Property Of One Point Compactification Then we have the following universal property: Theorem 2.3 a space has a. In bishop's constructive development of analysis, metric spaces are. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. To see a part of this, assume y is. The commutativity $f = \phi \circ g$ forces the definition of $g$: Let x x. Universal Property Of One Point Compactification.
From math.stackexchange.com
abstract algebra A difficulty in understanding the universal property Universal Property Of One Point Compactification In bishop's constructive development of analysis, metric spaces are. Let x x be a locally compact space, and let i: Then we have the following universal property: The commutativity $f = \phi \circ g$ forces the definition of $g$: Theorem 2.3 a space has a. To see a part of this, assume y is. Given a topological space x, we. Universal Property Of One Point Compactification.
From www.youtube.com
Universal property YouTube Universal Property Of One Point Compactification Given a topological space x, we wish to construct a compact space y by appending one point: To see a part of this, assume y is. The commutativity $f = \phi \circ g$ forces the definition of $g$: Let x x be a locally compact space, and let i: Theorem 2.3 a space has a. Then we have the following. Universal Property Of One Point Compactification.
From www.youtube.com
대수 03 _pre. Quotient field of an ID(Construction, Universal property Universal Property Of One Point Compactification Given a topological space x, we wish to construct a compact space y by appending one point: Let x x be a locally compact space, and let i: To see a part of this, assume y is. If $x \in x$, then $g(x) \in g[x]$ and $\phi$ must map $g(x)$ to. The commutativity $f = \phi \circ g$ forces the. Universal Property Of One Point Compactification.