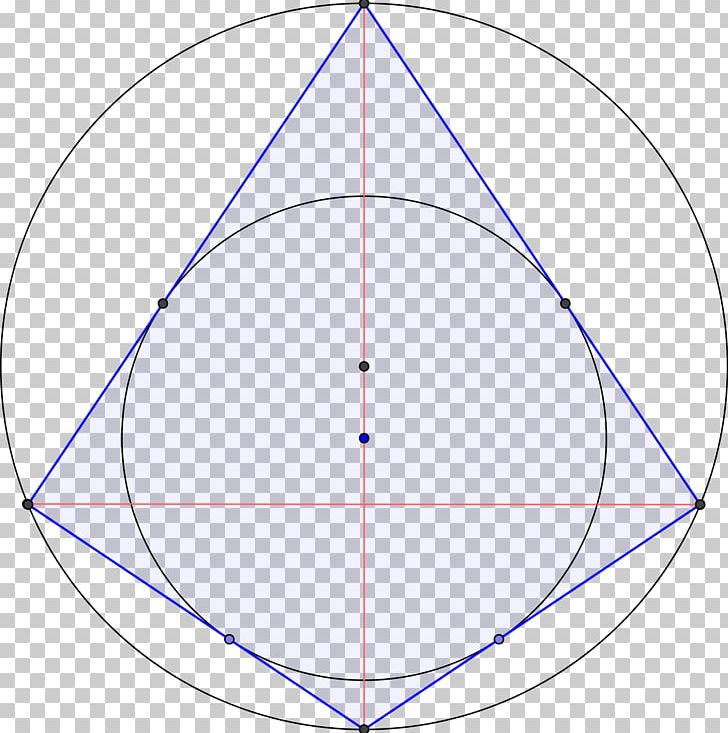
Can A Kite Be Inscribed In A Circle at Tina Rooney blog

Can A Kite Be Inscribed In A Circle. How exactly would one generalize the area of a kite inscribed within a circle? A kite is said to be right when it can be inscribed in a circle, that is, when the vertices are on a circumference. Prove kite, given circle and radii. The four points o, p, q, r are also the vertices of a kite, k. $a$, $b$, $c$ and $d$ lie in alphabetical order on a circle so that abcd forms a kite. The points o, p, q, r lie on a circle as shown in the diagram below. The kites that are also cyclic quadrilaterals (i.e. The question is as follows: Relative to the origin o, the coordinates. It is equivalent to saying that the circumference is circumscribed to the kite. See the problem statement, strategy and proof. Through a lot of calculation, which i do think was actually way more complicated then required,. $ab = da = 8 cm$. Oq is a diameter of the circle. 18 rows a kite with three equal 108° angles and one 36° angle forms the convex hull of the lute of pythagoras.

The kites that are also cyclic quadrilaterals (i.e. Oq is a diameter of the circle. The question is as follows: $ab = da = 8 cm$. Through a lot of calculation, which i do think was actually way more complicated then required,. A kite is said to be right when it can be inscribed in a circle, that is, when the vertices are on a circumference. The four points o, p, q, r are also the vertices of a kite, k. Prove kite, given circle and radii. Learn how to prove that when a kite is inscribed in a circle, the axis of symmetry of the kite is the diameter of the circle. 18 rows a kite with three equal 108° angles and one 36° angle forms the convex hull of the lute of pythagoras.

Right Kite Circle Inscribed Figure Quadrilateral PNG, Clipart, Angle

Can A Kite Be Inscribed In A Circle $a$, $b$, $c$ and $d$ lie in alphabetical order on a circle so that abcd forms a kite. How exactly would one generalize the area of a kite inscribed within a circle? 18 rows a kite with three equal 108° angles and one 36° angle forms the convex hull of the lute of pythagoras. The question is as follows: Oq is a diameter of the circle. Through a lot of calculation, which i do think was actually way more complicated then required,. Relative to the origin o, the coordinates. The points o, p, q, r lie on a circle as shown in the diagram below. $a$, $b$, $c$ and $d$ lie in alphabetical order on a circle so that abcd forms a kite. See the problem statement, strategy and proof. The kites that are also cyclic quadrilaterals (i.e. Prove kite, given circle and radii. It is equivalent to saying that the circumference is circumscribed to the kite. $ab = da = 8 cm$. A kite is said to be right when it can be inscribed in a circle, that is, when the vertices are on a circumference. Learn how to prove that when a kite is inscribed in a circle, the axis of symmetry of the kite is the diameter of the circle.