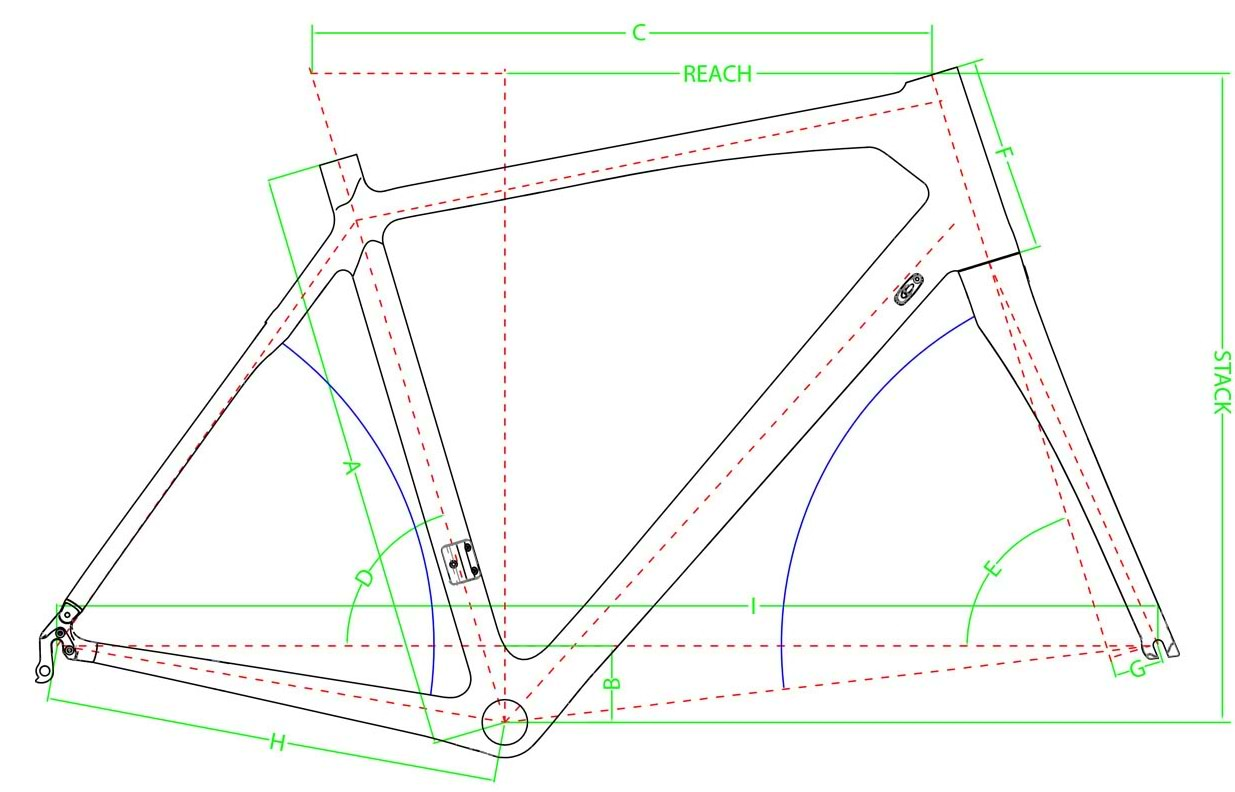
Cycle Definition Geometry . Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. This concept is crucial in. I receive a lot of questions about bicycle frame geometry, so. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. Suppose that x is an algebric variety of dimension d over a field f. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. It forms a closed loop or. An algebric cycle of dimension m in x is a formal.
from www.ribblecycles.co.uk
An algebric cycle of dimension m in x is a formal. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. I receive a lot of questions about bicycle frame geometry, so. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. Suppose that x is an algebric variety of dimension d over a field f. This concept is crucial in. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. It forms a closed loop or.
Bike Sizing Guide Ribble Cycles Ribble Cycles
Cycle Definition Geometry In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. An algebric cycle of dimension m in x is a formal. It forms a closed loop or. Suppose that x is an algebric variety of dimension d over a field f. This concept is crucial in. I receive a lot of questions about bicycle frame geometry, so. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated.
From biketips.com
Bike Geometry Explained A Beginner's Guide Cycle Definition Geometry It forms a closed loop or. Suppose that x is an algebric variety of dimension d over a field f. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. This concept is crucial in. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties. Cycle Definition Geometry.
From www.futura-sciences.com
Définition Cycle de Milankovitch Théorie de Milutin Milankovitch Cycle Definition Geometry In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. Suppose that x is an algebric variety of dimension d over a field f. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. This concept is crucial in. It. Cycle Definition Geometry.
From jralong.com
Making Sense of Bicycle Geometry Just Riding Along Cycle Definition Geometry In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. I receive a lot of questions about bicycle frame geometry, so. This concept is crucial in.. Cycle Definition Geometry.
From www.planetarycycles.com
Velotric T1 StepThru Cycles Houston, TX Bike Shop Cycle Definition Geometry Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. I receive a lot of questions about bicycle frame geometry, so. An algebric cycle of dimension m in x is. Cycle Definition Geometry.
From geometrygeeks.bike
Understanding Bike Geometry Cycle Definition Geometry In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. It forms a closed loop or. Suppose that x is an algebric variety of dimension d over a field f.. Cycle Definition Geometry.
From www.youtube.com
What are Hamiltonian Cycles and Paths? [Graph Theory] YouTube Cycle Definition Geometry In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. An algebric cycle of dimension m in x is a formal. This concept is crucial in. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. In graph theory, a. Cycle Definition Geometry.
From www.pinterest.com.mx
Circle Theorems for GCSE and iGCSE. More information and maths revision Cycle Definition Geometry In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. This concept is crucial in. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. In geometry, cycles refer to closed paths or circuits formed by a sequence of points. Cycle Definition Geometry.
From www.dreamstime.com
Geometric Cycle Diagrams with 3, 4, 5, 6, 7 and 8 Options, Steps or Cycle Definition Geometry I receive a lot of questions about bicycle frame geometry, so. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. Suppose that x is an. Cycle Definition Geometry.
From thecolcollective.com
Road Bike Geometry and What to Look For Learn The Col Collective Cycle Definition Geometry This concept is crucial in. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. I receive a lot of questions about bicycle frame geometry, so. Suppose that x is an algebric variety of dimension d over a field f. In graph theory, a cycle is a path that. Cycle Definition Geometry.
From notability.com
Euclidean Geometry Theorems Notability Gallery Cycle Definition Geometry A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. It forms a closed loop or. An algebric cycle of dimension m in x is a formal.. Cycle Definition Geometry.
From www.singletracks.com
MTB Frame Geometry Part 1 How It Fits Singletracks Mountain Bike News Cycle Definition Geometry An algebric cycle of dimension m in x is a formal. Suppose that x is an algebric variety of dimension d over a field f. It forms a closed loop or. This concept is crucial in. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. Algebraic cycles are. Cycle Definition Geometry.
From www.collinsdictionary.com
Cycle definition and meaning Collins English Dictionary Cycle Definition Geometry I receive a lot of questions about bicycle frame geometry, so. An algebric cycle of dimension m in x is a formal. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. In graph theory, a cycle is a path that starts and ends at the same vertex while. Cycle Definition Geometry.
From www.batchbicycles.com
The Kids Bicycle Geometry Chart Batch Bicycles Cycle Definition Geometry Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. I receive a lot of questions about bicycle frame geometry, so. A cycle in graph theory is a path that. Cycle Definition Geometry.
From www.cazoommaths.com
Proving Circle Theorems Cyclic Quadrilaterals Worksheet Fun and Cycle Definition Geometry Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. Suppose that x is an algebric variety of dimension d over a field f. I receive a lot of questions about bicycle frame geometry, so. This concept is crucial in. A cycle in graph theory is a path that starts and ends. Cycle Definition Geometry.
From recklesscognition.wordpress.com
Bicycle geometry. A brief look into how it effects your ride. Bicycle Cycle Definition Geometry An algebric cycle of dimension m in x is a formal. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. I receive a lot of questions about bicycle frame geometry, so. Suppose that x is an algebric variety of dimension d over a field f. In geometry, cycles. Cycle Definition Geometry.
From www.youtube.com
Definition of Chords in Cycles Graph Theory, Chordless Cycles YouTube Cycle Definition Geometry Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. It forms a closed loop or. An algebric cycle of dimension m in x is a formal. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. In geometry, cycles refer. Cycle Definition Geometry.
From www.cyclingweekly.com
Mountain bike versus hybrid What's the difference? review Cycling Weekly Cycle Definition Geometry This concept is crucial in. Suppose that x is an algebric variety of dimension d over a field f. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. I receive a lot of questions about bicycle frame geometry, so. An algebric cycle of dimension m in x is a formal. It. Cycle Definition Geometry.
From electricbikeaction.com
The Importance of Mountain Bike Geometry Electric Bike Action Cycle Definition Geometry In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. This concept is crucial in. It forms a closed loop or. A cycle in graph theory. Cycle Definition Geometry.
From mungfali.com
Geometry All Circle Theorems Cycle Definition Geometry It forms a closed loop or. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. I receive a lot of questions about bicycle frame geometry, so. This concept is. Cycle Definition Geometry.
From www.pinterest.com.au
Geometry and Measures Posters Math poster, Circle theorems, Math charts Cycle Definition Geometry Suppose that x is an algebric variety of dimension d over a field f. This concept is crucial in. An algebric cycle of dimension m in x is a formal. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. It forms a closed loop or. In geometry, cycles. Cycle Definition Geometry.
From blog.jonesbikes.com
Spaceframe Geometry Jones Bikes Blog Cycle Definition Geometry Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. It forms a closed loop or. I receive a lot of questions about bicycle frame geometry, so. An algebric cycle. Cycle Definition Geometry.
From www.semanticscholar.org
Figure 1 from Cycles and components in geometric graphs adjacency Cycle Definition Geometry An algebric cycle of dimension m in x is a formal. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. It forms a closed loop or.. Cycle Definition Geometry.
From www.ma.utexas.edu
Algebraic Cycles Cycle Definition Geometry In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices. Cycle Definition Geometry.
From triaero.com
The Beginners Guide to Road Bike Geometry Triaero Cycle Definition Geometry In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. This concept is crucial in. Suppose that x is an algebric variety of dimension d over a field f. An algebric cycle of dimension m in x is a formal. A cycle in graph theory is a path. Cycle Definition Geometry.
From peacecommission.kdsg.gov.ng
Understanding Bike Frame Geometry USJ CYCLES Cycle Definition Geometry Suppose that x is an algebric variety of dimension d over a field f. It forms a closed loop or. An algebric cycle of dimension m in x is a formal. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. A cycle in graph theory is a. Cycle Definition Geometry.
From www.universalcycles.com
Universal Cycles Sizing and Geometry Charts Cycle Definition Geometry This concept is crucial in. It forms a closed loop or. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. Suppose that x is an algebric variety of dimension d over a field f. An algebric cycle of dimension m in x is a formal. Algebraic cycles are. Cycle Definition Geometry.
From www.universalcycles.com
Universal Cycles Sizing and Geometry Charts Cycle Definition Geometry An algebric cycle of dimension m in x is a formal. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. It forms a closed loop or. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. This concept is. Cycle Definition Geometry.
From www.stevehoggbikefitting.com
FRAME GEOMETRY FOR ROAD BIKES How it all works The Steve Hogg Bike Cycle Definition Geometry It forms a closed loop or. I receive a lot of questions about bicycle frame geometry, so. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. An algebric cycle of dimension m in x is a formal. This concept is crucial in. Suppose that x is an algebric variety of dimension. Cycle Definition Geometry.
From www.yellowjersey.co.uk
Bike Geometry Explained Cycle Definition Geometry In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. Suppose that x is an algebric variety of dimension d over a field f. A cycle. Cycle Definition Geometry.
From www.merkabici.es
Bike geometry Everything you need to know about it Merkabici Cycle Definition Geometry Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. This concept is crucial in. It forms a closed loop or. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. An algebric cycle of dimension m in x is. Cycle Definition Geometry.
From www.yellowjersey.co.uk
Bike Geometry Explained Cycle Definition Geometry I receive a lot of questions about bicycle frame geometry, so. This concept is crucial in. A cycle in graph theory is a path that starts and ends at the same vertex with no other vertices repeated. An algebric cycle of dimension m in x is a formal. It forms a closed loop or. In graph theory, a cycle is. Cycle Definition Geometry.
From www.ribblecycles.co.uk
Bike Sizing Guide Ribble Cycles Ribble Cycles Cycle Definition Geometry Suppose that x is an algebric variety of dimension d over a field f. It forms a closed loop or. In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. This concept is crucial in. An algebric cycle of dimension m in x is a formal. I receive. Cycle Definition Geometry.
From bmp-willy.blogspot.com
Measure Of An Angle Definition Geometry / Angles are measured with Cycle Definition Geometry It forms a closed loop or. I receive a lot of questions about bicycle frame geometry, so. Algebraic cycles are crucial in defining intersection numbers, which represent how two subvarieties intersect within a given variety,. This concept is crucial in. An algebric cycle of dimension m in x is a formal. A cycle in graph theory is a path that. Cycle Definition Geometry.
From bikexchange.com
Bicycle Geometry 101 Guide Cycle Definition Geometry Suppose that x is an algebric variety of dimension d over a field f. An algebric cycle of dimension m in x is a formal. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. A cycle in graph theory is a path that starts and ends at. Cycle Definition Geometry.
From www.bikecad.ca
Measuring realworld bicycle geometry www.bikecad.ca Cycle Definition Geometry In graph theory, a cycle is a path that starts and ends at the same vertex while visiting other vertices exactly once. Suppose that x is an algebric variety of dimension d over a field f. In geometry, cycles refer to closed paths or circuits formed by a sequence of points connected by edges, creating a loop without. A cycle. Cycle Definition Geometry.