Boundary Of Point Set . a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real numbers not in. \(d\) is said to be open if. boundary point of a set. boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). a point which is a member of the set closure of a given set s and the set closure of its complement set. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary.
from calcworkshop.com
the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). a point which is a member of the set closure of a given set s and the set closure of its complement set. \(d\) is said to be open if. boundary point of a set. a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real numbers not in. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement.
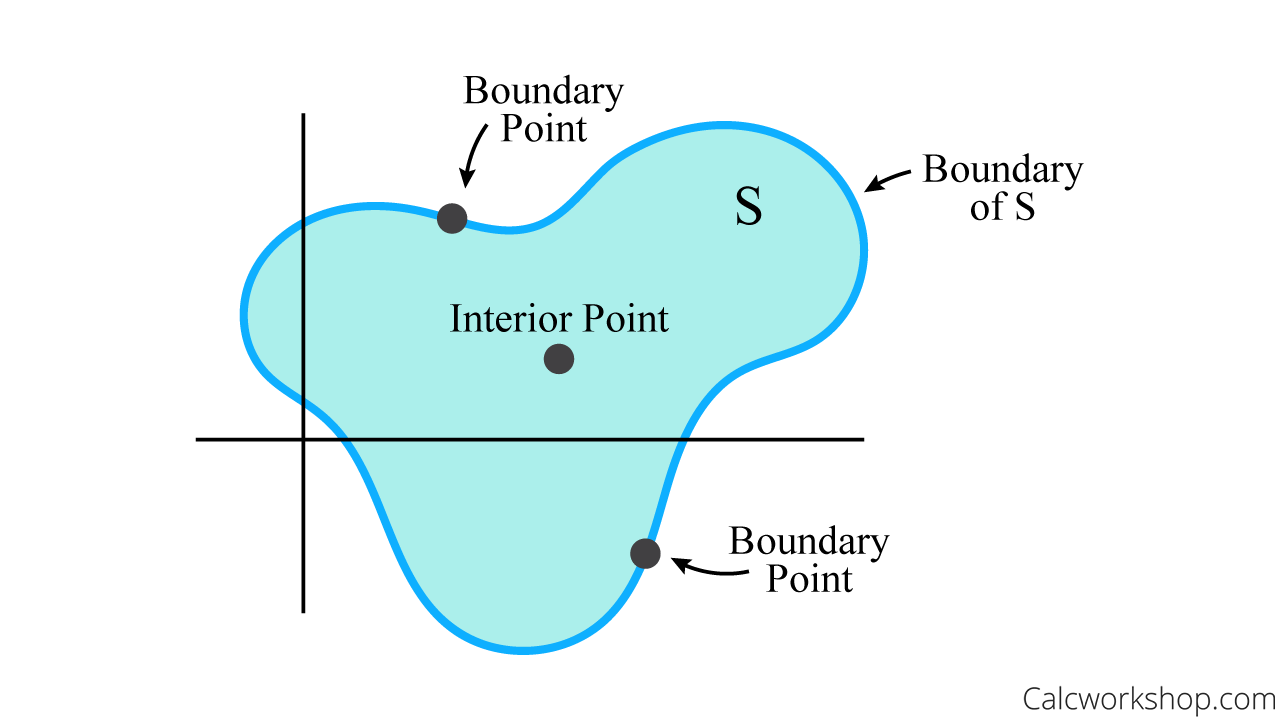
Extrema Of Multivariable Functions (Explained w/ StepbyStep Examples!)
Boundary Of Point Set a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. \(d\) is said to be open if. a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real numbers not in. a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a point which is a member of the set closure of a given set s and the set closure of its complement set. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). boundary point of a set.
From www.researchgate.net
Building boundary of point set by Alpha Shapes algorithm. Download Boundary Of Point Set a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. a point which is a member of the set closure of a given set s and the set closure of its complement set. \(d\) is said to be open if. boundary. Boundary Of Point Set.
From www.youtube.com
Interior Point, Exterior Point, Boundary Point, Isolated Point, Limit Boundary Of Point Set boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the. Boundary Of Point Set.
From www.slideserve.com
PPT Chapter 2 Linear Relations & Functions PowerPoint Presentation Boundary Of Point Set \(d\) is said to be open if. a point which is a member of the set closure of a given set s and the set closure of its complement set. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. boundary of a. Boundary Of Point Set.
From www.youtube.com
Frontier/Boundary Points with exampleHow to find frontier points Boundary Of Point Set \(d\) is said to be open if. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. . Boundary Of Point Set.
From mathoverflow.net
mg.metric geometry Determine the boundary points of a set of points Boundary Of Point Set a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real numbers not in. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). \(d\) is said to be open if. boundary. Boundary Of Point Set.
From www.youtube.com
Solve the Quadratic Inequality Using Boundary Points (Critical Points Boundary Of Point Set a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a boundary point of a set \(s\). Boundary Of Point Set.
From github.com
GitHub Geodan/buildingboundary Traces the boundary of a set of Boundary Of Point Set boundary point of a set. a point which is a member of the set closure of a given set s and the set closure of its complement set. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. boundary of a set. Boundary Of Point Set.
From avidemia.com
3.4 Open and Closed Sets Avidemia Boundary Of Point Set a point which is a member of the set closure of a given set s and the set closure of its complement set. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. boundary of a set as the set of points all. Boundary Of Point Set.
From www.youtube.com
401.8 Isolated and boundary points YouTube Boundary Of Point Set Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. \(d\) is said to be open if. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). a point which is a. Boundary Of Point Set.
From stackoverflow.com
python How to get the mean curve(a set of points) of a boundary(a set Boundary Of Point Set boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. a point which is a member of the set closure of. Boundary Of Point Set.
From www.youtube.com
Solve a Quadratic Inequality Using Boundary Points (Critical Points) EX Boundary Of Point Set a point which is a member of the set closure of a given set s and the set closure of its complement set. a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. boundary of a set as the set of. Boundary Of Point Set.
From www.researchgate.net
An example of boundary points. The dataset is divided into two Boundary Of Point Set the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. a boundary point of a set \(s\) of real numbers is one that is a limit. Boundary Of Point Set.
From www.researchgate.net
A set of equations is formulated at a set of boundary points chosen on Boundary Of Point Set a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real numbers not in. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). a boundary point is, therefore, a point all. Boundary Of Point Set.
From www.youtube.com
Boundary points and boundary of a set in Topology YouTube Boundary Of Point Set a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. a boundary point of a set \(s\) of real numbers is. Boundary Of Point Set.
From math.stackexchange.com
metric spaces Understanding the idea of a Limit Point (Topology Boundary Of Point Set a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). boundary point of a set. a point which is. Boundary Of Point Set.
From www.numerade.com
SOLVED Prove A limit point of a set S is either a interior point Or Boundary Of Point Set a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. \(d\) is said to be open if. a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real. Boundary Of Point Set.
From www.pngwing.com
Boundary Point Topological space Topology Closed set, boundary, angle Boundary Of Point Set \(d\) is said to be open if. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a boundary point is, therefore,. Boundary Of Point Set.
From gis.stackexchange.com
qgis Converting point sets to polygon boundaries? Geographic Boundary Of Point Set a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a point which is a member of. Boundary Of Point Set.
From www.slideserve.com
PPT MAT 3730 Complex Variables PowerPoint Presentation, free download Boundary Of Point Set \(d\) is said to be open if. a point which is a member of the set closure of a given set s and the set closure of its complement set. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a boundary point. Boundary Of Point Set.
From www.youtube.com
Finding the Interior, Exterior, and Boundary of a Set Topology YouTube Boundary Of Point Set a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. boundary point of a set. a point which is a member of the set closure of a given set s and the set closure of its complement set. \(d\) is said. Boundary Of Point Set.
From www.youtube.com
Metric Spaces (BOUNDED SETS, BOUNDARY OF A SET & CONTINUOUS MAPPINGS Boundary Of Point Set the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. Let a a be a subset of a topological space x. Boundary Of Point Set.
From www.researchgate.net
Figure shows more examples of 2D Points sets and the decision boundary Boundary Of Point Set the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. boundary of a set as the set of points all of whose. Boundary Of Point Set.
From imgbin.com
Interior Point Open Set Boundary PNG, Clipart, Area, Boundary, Closure Boundary Of Point Set a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. \(d\) is said to be open if. boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. a boundary point of. Boundary Of Point Set.
From gis.stackexchange.com
qgis Converting point sets to polygon boundaries? Geographic Boundary Of Point Set Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). \(d\) is said to be open if. a boundary point is, therefore,. Boundary Of Point Set.
From www.slideserve.com
PPT Topology PowerPoint Presentation, free download ID9252540 Boundary Of Point Set a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real numbers not in. a point which is a member of the set closure of a given set s and the set closure of its complement set. Let a a be a subset of. Boundary Of Point Set.
From www.youtube.com
Geometry, Level 4 of 6, Example 1, Interior and boundary points of Boundary Of Point Set \(d\) is said to be open if. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. . Boundary Of Point Set.
From www.researchgate.net
Instance point with adjacent points in the pointset domain of the Boundary Of Point Set \(d\) is said to be open if. a point which is a member of the set closure of a given set s and the set closure of its complement set. boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. a boundary point is, therefore, a point. Boundary Of Point Set.
From www.everydayhealth.com
Boundary Setting What It Is, Why It’s Good for You, and How to Practice It Boundary Of Point Set \(d\) is said to be open if. a point which is a member of the set closure of a given set s and the set closure of its complement set. boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. a boundary point is, therefore, a point. Boundary Of Point Set.
From www.youtube.com
3 Operations on functions Interior point Boundary point C7 Boundary Of Point Set boundary point of a set. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a boundary point is, therefore, a. Boundary Of Point Set.
From www.youtube.com
Closure of a set in a topological space Dense Set Suppose Math with Boundary Of Point Set a point which is a member of the set closure of a given set s and the set closure of its complement set. \(d\) is said to be open if. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). boundary of a set as the. Boundary Of Point Set.
From www.youtube.com
Verification of all properties of Boundary points of a set with an Boundary Of Point Set a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real numbers not in. \(d\) is said to be open if. a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point. Boundary Of Point Set.
From calcworkshop.com
Extrema Of Multivariable Functions (Explained w/ StepbyStep Examples!) Boundary Of Point Set \(d\) is said to be open if. a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real numbers not in. the set of interior points in d constitutes its interior, \(\mathrm{int}(d)\), and the set of boundary points its boundary, \(\partial d\). a. Boundary Of Point Set.
From www.researchgate.net
Showing the region and boundary as the set of critical points where the Boundary Of Point Set a point which is a member of the set closure of a given set s and the set closure of its complement set. \(d\) is said to be open if. boundary point of a set. boundary of a set as the set of points all of whose neighborhoods intersect both the set and its complement. the. Boundary Of Point Set.
From stackoverflow.com
python Boundary points from a set of coordinates Stack Overflow Boundary Of Point Set \(d\) is said to be open if. boundary point of a set. Let a a be a subset of a topological space x x, a point x ∈ x x ∈ x is said to be boundary. a point which is a member of the set closure of a given set s and the set closure of its. Boundary Of Point Set.
From www.youtube.com
Isolated and accumulation points YouTube Boundary Of Point Set a boundary point of a set \(s\) of real numbers is one that is a limit point both of \(s\) and the set of real numbers not in. a boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in s and at least one point not in s. a point which. Boundary Of Point Set.