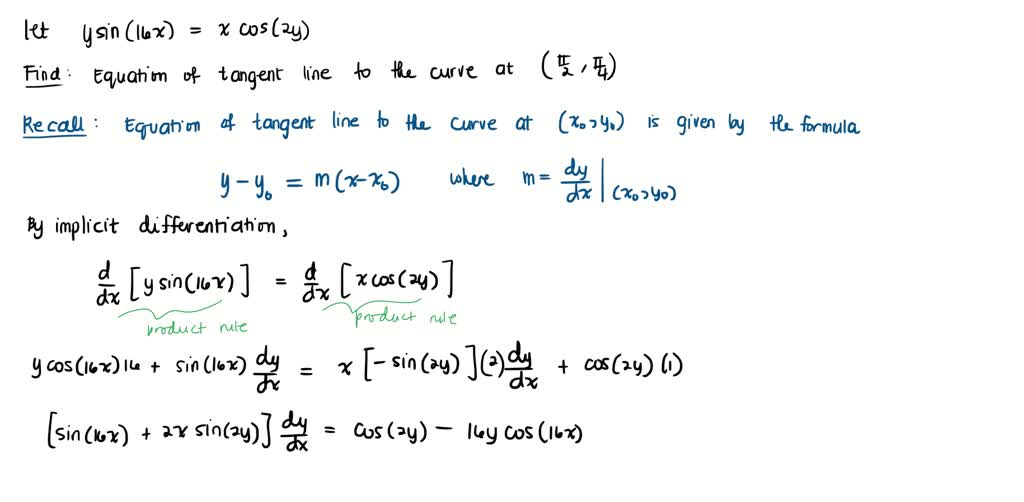Tangent Line Using Implicit Differentiation . Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). We have already studied how to find equations of. Collect all the dy dx on one side. Using implicit differentiation to find a tangent line. So here are a few examples finding the equations of tangent lines to. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ Differentiate with respect to x: How to do implicit differentiation. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). Use implicit differentiation to determine the equation of a tangent line. Differentiate with respect to x. The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. D dx (x 2) + d dx (y 2) = d. X 2 + y 2 = r 2. By using implicit differentiation, we can find the equation of a tangent.
from www.numerade.com
Use implicit differentiation to determine the equation of a tangent line. Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ Differentiate with respect to x. Collect all the dy dx on one side. D dx (x 2) + d dx (y 2) = d. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). By using implicit differentiation, we can find the equation of a tangent. We have already studied how to find equations of. Using implicit differentiation to find a tangent line.
SOLVED Use implicit differentiation to find an equation of the tangent
Tangent Line Using Implicit Differentiation We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). So here are a few examples finding the equations of tangent lines to. Differentiate with respect to x. By using implicit differentiation, we can find the equation of a tangent. Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). D dx (x 2) + d dx (y 2) = d. Using implicit differentiation to find a tangent line. Collect all the dy dx on one side. Differentiate with respect to x: X 2 + y 2 = r 2. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. We have already studied how to find equations of. Use implicit differentiation to determine the equation of a tangent line. How to do implicit differentiation. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$
From www.youtube.com
How to find the tangent line at a specific point using Implicit Tangent Line Using Implicit Differentiation D dx (x 2) + d dx (y 2) = d. By using implicit differentiation, we can find the equation of a tangent. X 2 + y 2 = r 2. Differentiate with respect to x. The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. Differentiate with respect to x:. Tangent Line Using Implicit Differentiation.
From www.numerade.com
SOLVED 'Show, using implicit differentiation; that any tangent line at Tangent Line Using Implicit Differentiation Using implicit differentiation to find a tangent line. By using implicit differentiation, we can find the equation of a tangent. So here are a few examples finding the equations of tangent lines to. How to do implicit differentiation. X 2 + y 2 = r 2. The typical way to get used to implicit differentiation is to play with problems. Tangent Line Using Implicit Differentiation.
From www.wikihow.com
How to Do Implicit Differentiation 7 Steps (with Pictures) Tangent Line Using Implicit Differentiation We have already studied how to find equations of. How to do implicit differentiation. Differentiate with respect to x: Collect all the dy dx on one side. Differentiate with respect to x. Use implicit differentiation to determine the equation of a tangent line. So here are a few examples finding the equations of tangent lines to. D dx (x 2). Tangent Line Using Implicit Differentiation.
From www.youtube.com
MAT190 Chapter 3 Equation of a Tangent Line Using Implicit Tangent Line Using Implicit Differentiation Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ So here are a few examples finding the equations of tangent lines to. Collect all the dy dx on one side. By using implicit differentiation, we can find the equation of a tangent. Differentiate with respect to x. X 2 +. Tangent Line Using Implicit Differentiation.
From www.numerade.com
SOLVED point) Use implicit differentiation to find an equation of the Tangent Line Using Implicit Differentiation How to do implicit differentiation. Collect all the dy dx on one side. Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). Differentiate with respect to x: The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. By. Tangent Line Using Implicit Differentiation.
From www.youtube.com
equation of the tangent line to the ellipse using implicit Tangent Line Using Implicit Differentiation Use implicit differentiation to determine the equation of a tangent line. D dx (x 2) + d dx (y 2) = d. The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. Using implicit differentiation to find a tangent line. X 2 + y 2 = r 2. Differentiate with respect. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Implicit Differentiation Example Locations of Horizontal and Vertical Tangent Line Using Implicit Differentiation X 2 + y 2 = r 2. Use implicit differentiation to determine the equation of a tangent line. How to do implicit differentiation. The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. By using implicit differentiation, we can find the equation of a tangent. Using implicit differentiation to find. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Find equation of tangent line using implicit differentiation to find Tangent Line Using Implicit Differentiation How to do implicit differentiation. Collect all the dy dx on one side. Using implicit differentiation to find a tangent line. Differentiate with respect to x. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). Use implicit differentiation to determine the equation of a tangent line. X 2 + y 2 = r 2.. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Cu3L4b Implicit Differentiation pt II Vertical and Horizontal Tangent Tangent Line Using Implicit Differentiation Collect all the dy dx on one side. The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). How to do implicit differentiation. So here are a few examples. Tangent Line Using Implicit Differentiation.
From www.numerade.com
SOLVEDShow, using implicit differentiation, that any tangent line at a Tangent Line Using Implicit Differentiation Collect all the dy dx on one side. Using implicit differentiation to find a tangent line. How to do implicit differentiation. Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). Differentiate with respect to x. Differentiate with respect to x: We have already studied how to find. Tangent Line Using Implicit Differentiation.
From mathsathome.com
How to Find the Equation of a Tangent Line Tangent Line Using Implicit Differentiation By using implicit differentiation, we can find the equation of a tangent. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). The typical way to get used to implicit differentiation is to play with problems. Tangent Line Using Implicit Differentiation.
From www.pinterest.com
Equation of the Tangent Line with Implicit Differentiation Example 4 Tangent Line Using Implicit Differentiation Collect all the dy dx on one side. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ Using implicit differentiation to find a tangent line. We have already studied how to find equations of. The typical way to get used to implicit differentiation is to play with problems involving tangent. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Implicit Differentiation Finding an equation of the tangent line at a Tangent Line Using Implicit Differentiation Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). Collect all the dy dx on one side. Differentiate with respect to x: Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ Using implicit differentiation to find a. Tangent Line Using Implicit Differentiation.
From www.coursehero.com
[Solved] Use implicit differentiation to find the equation of the Tangent Line Using Implicit Differentiation Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). So here are a few examples finding the equations of tangent lines to. Using implicit differentiation to find a tangent line. Differentiate with respect to x. By using implicit differentiation, we can find the equation of a tangent.. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Equation of the Tangent Line with Implicit Differentiation Example 4 Tangent Line Using Implicit Differentiation Using implicit differentiation to find a tangent line. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). Use implicit differentiation to determine the equation of a tangent line.. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Tangent Line Using Implicit Differentiation YouTube Tangent Line Using Implicit Differentiation X 2 + y 2 = r 2. Differentiate with respect to x: Using implicit differentiation to find a tangent line. We have already studied how to find equations of. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). Differentiate with respect to x. The typical way to get used to implicit differentiation is. Tangent Line Using Implicit Differentiation.
From www.youtube.com
HOW TO FIND EQUATION OF TANGENT LINE WITH IMPLICIT DIFFERENTIATION Tangent Line Using Implicit Differentiation Differentiate with respect to x: Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). X 2 + y 2 = r 2. The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. Use implicit differentiation to find an. Tangent Line Using Implicit Differentiation.
From www.nagwa.com
Question Video Finding the Equation of the Tangent to a Curve Defined Tangent Line Using Implicit Differentiation By using implicit differentiation, we can find the equation of a tangent. Differentiate with respect to x. We have already studied how to find equations of. How to do implicit differentiation. Collect all the dy dx on one side. D dx (x 2) + d dx (y 2) = d. We use implicit differentiation to find derivatives of implicitly defined. Tangent Line Using Implicit Differentiation.
From www.youtube.com
How to use implicit differentiation to find an equation of the tangent Tangent Line Using Implicit Differentiation Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ Differentiate with respect to x. We have already studied how to find equations of. X 2 + y 2 = r 2. By using implicit differentiation, we can find the equation of a tangent. Use implicit differentiation to determine the equation. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Findinding the Tangent Line Using Implicit Differentiation. Openstax Tangent Line Using Implicit Differentiation Collect all the dy dx on one side. Differentiate with respect to x. Using implicit differentiation to find a tangent line. Differentiate with respect to x: Use implicit differentiation to determine the equation of a tangent line. We have already studied how to find equations of. Use implicit differentiation to find an equation of the tangent line to the curve. Tangent Line Using Implicit Differentiation.
From www.kristakingmath.com
Equation of the tangent line using implicit differentiation — Krista Tangent Line Using Implicit Differentiation Collect all the dy dx on one side. The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. By using implicit differentiation, we can find the equation of a tangent. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ We use. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Equation of the Tangent Line Using Implicit Differentiation Calculus 1 Tangent Line Using Implicit Differentiation We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). Collect all the dy dx on one side. So here are a few examples finding the equations of tangent lines to. Use implicit differentiation to determine the equation of a tangent line. Differentiate with respect to x. Using implicit differentiation to find a tangent line.. Tangent Line Using Implicit Differentiation.
From www.numerade.com
SOLVED Find the equation of the tangent line to the curve at the given Tangent Line Using Implicit Differentiation D dx (x 2) + d dx (y 2) = d. Differentiate with respect to x. So here are a few examples finding the equations of tangent lines to. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). We have already studied how to find equations of. By using implicit differentiation, we can find. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Derivatives 20 Finding Tangent Lines Using Implicit Differentiation Tangent Line Using Implicit Differentiation The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. We have already studied how to find equations of. Differentiate with respect to x: Collect all the dy dx on one side. D dx (x 2) + d dx (y 2) = d. Using implicit differentiation to find a tangent line.. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Tangent Line and Implicit Differentiation Finding Equation of Tangent Tangent Line Using Implicit Differentiation D dx (x 2) + d dx (y 2) = d. Use implicit differentiation to determine the equation of a tangent line. Differentiate with respect to x: Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by. Tangent Line Using Implicit Differentiation.
From www.numerade.com
SOLVED Use implicit differentiation to find an equation of the tangent Tangent Line Using Implicit Differentiation X 2 + y 2 = r 2. By using implicit differentiation, we can find the equation of a tangent. We have already studied how to find equations of. Differentiate with respect to x: Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ So here are a few examples finding. Tangent Line Using Implicit Differentiation.
From www.youtube.com
equations of tangent line and normal line using implicit Tangent Line Using Implicit Differentiation So here are a few examples finding the equations of tangent lines to. We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). Collect all the dy dx on one side. By using implicit differentiation, we can find the equation of a tangent. Use implicit differentiation to determine the equation of a tangent line. Differentiate. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Using implicit differentiation to find the equation of tangent line Tangent Line Using Implicit Differentiation Use implicit differentiation to determine the equation of a tangent line. How to do implicit differentiation. The typical way to get used to implicit differentiation is to play with problems involving tangent lines to curves. By using implicit differentiation, we can find the equation of a tangent. Use implicit differentiation to find an equation of the tangent line to the. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Find equation of tangent line with implicit differentiation for x^2 Tangent Line Using Implicit Differentiation By using implicit differentiation, we can find the equation of a tangent. So here are a few examples finding the equations of tangent lines to. How to do implicit differentiation. Use implicit differentiation to determine the equation of a tangent line. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$. Tangent Line Using Implicit Differentiation.
From www.numerade.com
SOLVED 'Show, using implicit differentiation, that any tangent line at Tangent Line Using Implicit Differentiation Differentiate with respect to x: Collect all the dy dx on one side. Differentiate with respect to x. D dx (x 2) + d dx (y 2) = d. Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). So here are a few examples finding the equations. Tangent Line Using Implicit Differentiation.
From www.youtube.com
Tangent Line, Implicit Differentiation Horizontal and Vertical Tangent Tangent Line Using Implicit Differentiation So here are a few examples finding the equations of tangent lines to. Collect all the dy dx on one side. Differentiate with respect to x. Use implicit differentiation to determine the equation of a tangent line. Differentiate with respect to x: How to do implicit differentiation. D dx (x 2) + d dx (y 2) = d. Use implicit. Tangent Line Using Implicit Differentiation.
From www.numerade.com
SOLVED Use implicit differentiation to find an equation for the Tangent Line Using Implicit Differentiation Collect all the dy dx on one side. Differentiate with respect to x: How to do implicit differentiation. By using implicit differentiation, we can find the equation of a tangent. So here are a few examples finding the equations of tangent lines to. The typical way to get used to implicit differentiation is to play with problems involving tangent lines. Tangent Line Using Implicit Differentiation.
From www.youtube.com
3.6 Implicit Differentiation (Equation of a Tangent Line) YouTube Tangent Line Using Implicit Differentiation So here are a few examples finding the equations of tangent lines to. Use implicit differentiation to find an equation of the tangent line to the curve at the given point $(2,4)$ D dx (x 2) + d dx (y 2) = d. Use implicit differentiation to determine the equation of a tangent line. By using implicit differentiation, we can. Tangent Line Using Implicit Differentiation.
From www.pinterest.com
Equation of the Tangent Line with Implicit Differentiation x^2 Tangent Line Using Implicit Differentiation How to do implicit differentiation. D dx (x 2) + d dx (y 2) = d. Differentiate with respect to x. Use implicit differentiation to determine the equation of a tangent line. Using implicit differentiation to find a tangent line. Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical. Tangent Line Using Implicit Differentiation.
From www.numerade.com
SOLVED Find an equation of the tangent line to the graph of the Tangent Line Using Implicit Differentiation Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). We use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). D dx (x 2) + d dx (y 2) = d. By using implicit differentiation, we can find the equation of a tangent.. Tangent Line Using Implicit Differentiation.