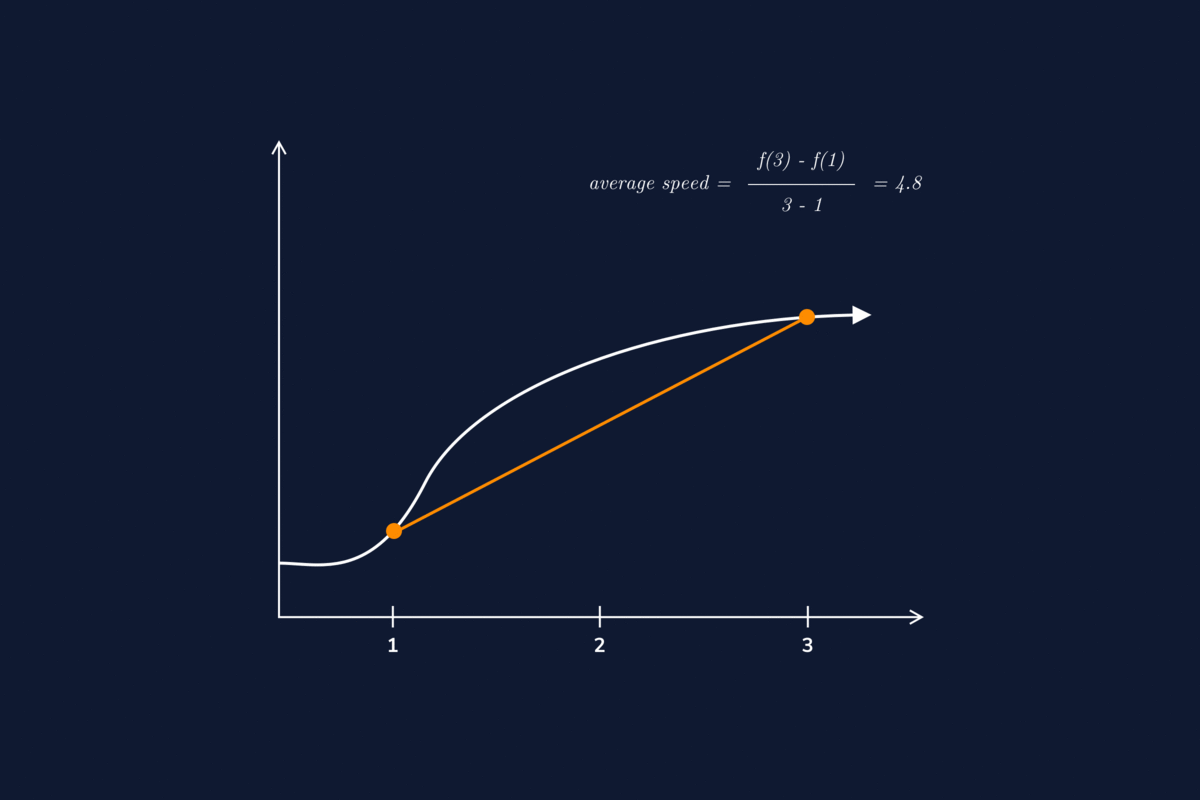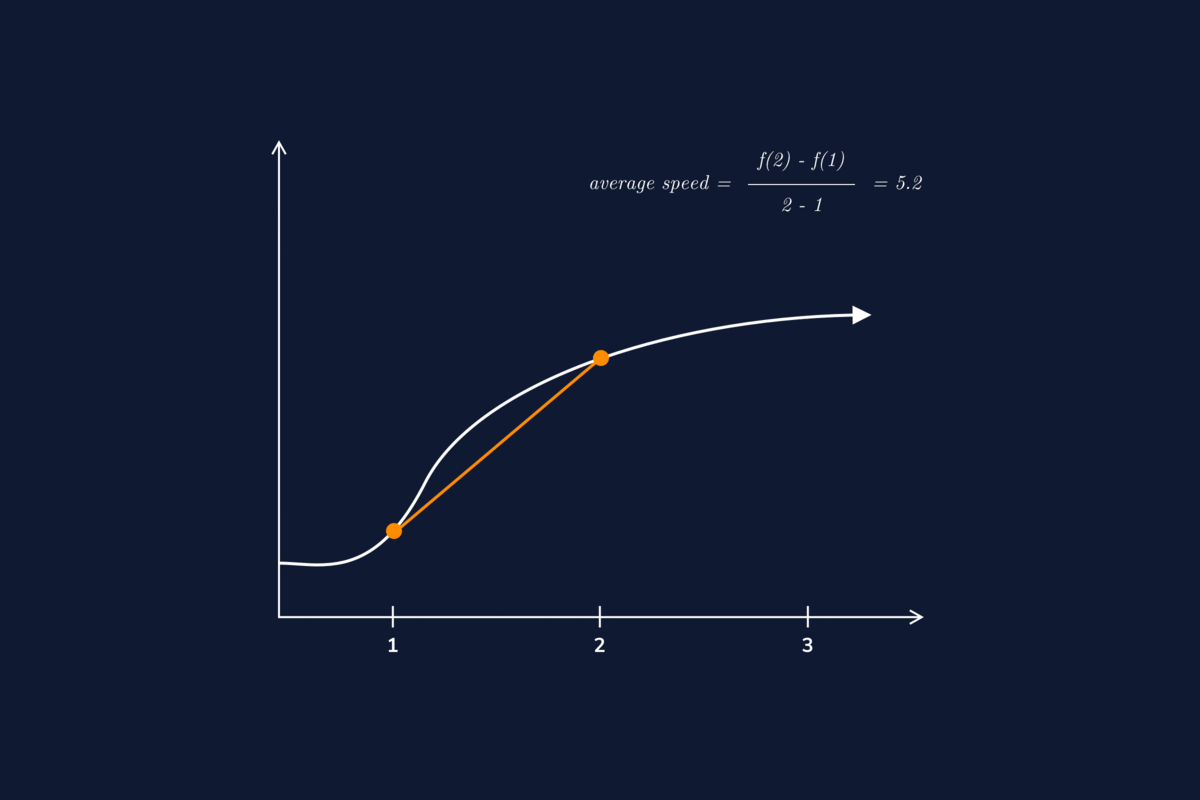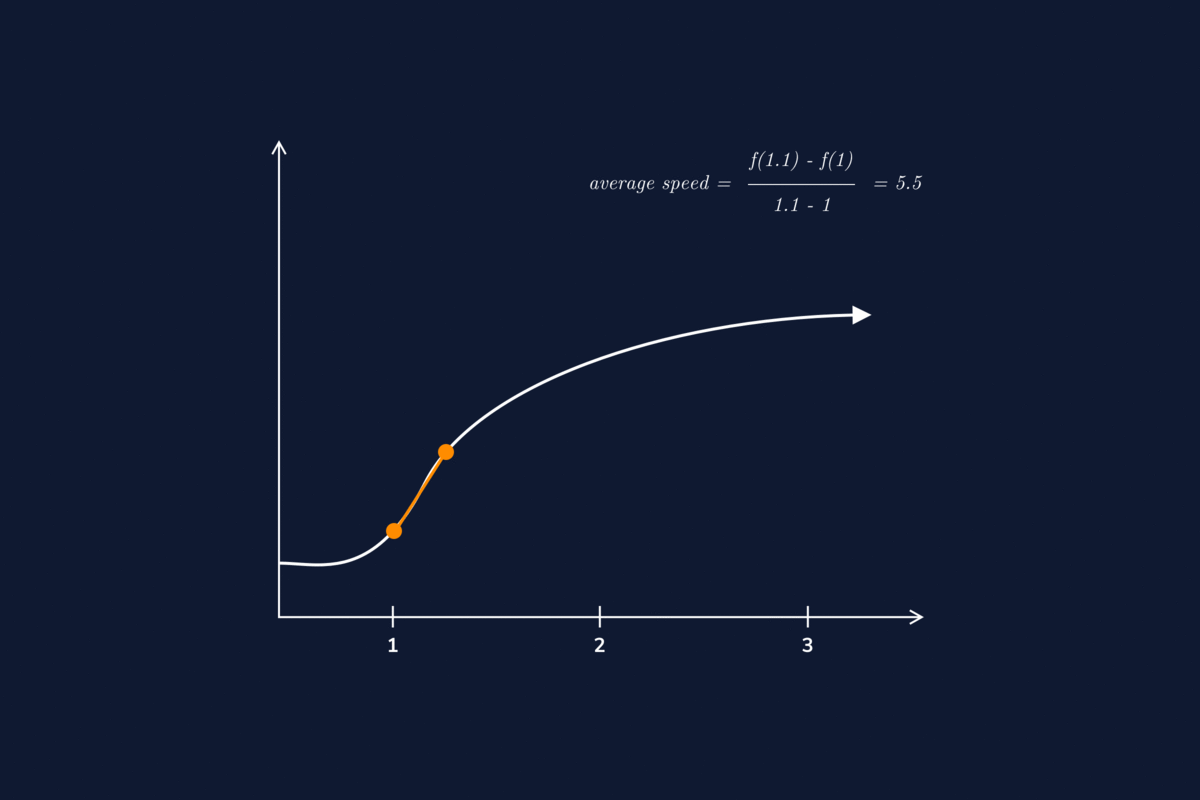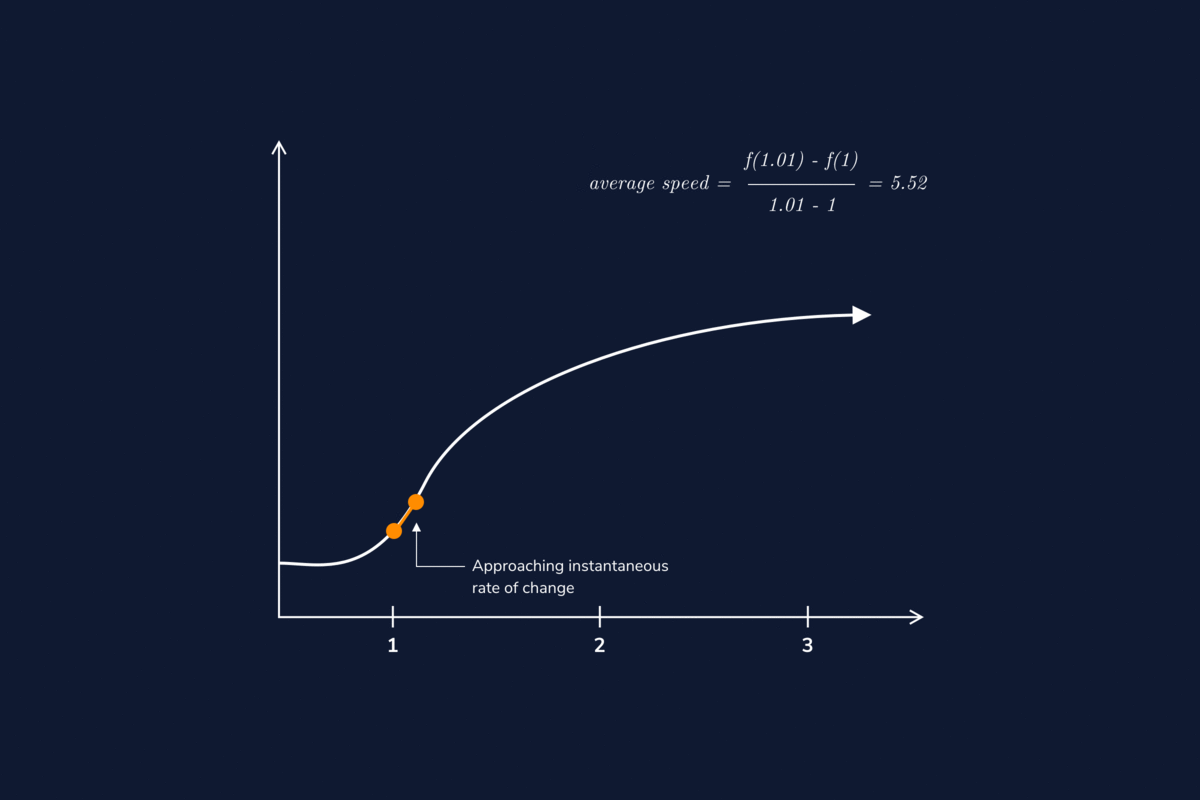Differential Velocity Calculus . Example 3.1.1 velocity as derivative of position. But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. Displacement, velocity and acceleration can be expressed as functions of time. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. Integral calculus gives us a more complete formulation of kinematics. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). Chapter 10 velocity, acceleration, and calculus. The first derivative of position is velocity, and the second derivative is acceleration. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Connection at the center of differential calculus. If we express these quantities as functions, they can be related by derivatives.
from www.codecademy.com
If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Connection at the center of differential calculus. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. Integral calculus gives us a more complete formulation of kinematics. Example 3.1.1 velocity as derivative of position. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. Displacement, velocity and acceleration can be expressed as functions of time. Chapter 10 velocity, acceleration, and calculus. If we express these quantities as functions, they can be related by derivatives.
Differential Calculus Differential Calculus Cheatsheet Codecademy
Differential Velocity Calculus If we express these quantities as functions, they can be related by derivatives. But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. Displacement, velocity and acceleration can be expressed as functions of time. Integral calculus gives us a more complete formulation of kinematics. If we express these quantities as functions, they can be related by derivatives. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. The first derivative of position is velocity, and the second derivative is acceleration. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. Example 3.1.1 velocity as derivative of position. Connection at the center of differential calculus. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Chapter 10 velocity, acceleration, and calculus. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\).
From www.showme.com
Examples with Displacement, Velocity and Acceleration Math, MOTION Differential Velocity Calculus In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. Chapter 10 velocity, acceleration, and calculus. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Let \(r(t)\) be a differentiable. Differential Velocity Calculus.
From www.youtube.com
Terminal velocity differential equation Lecture 8 Differential Differential Velocity Calculus Integral calculus gives us a more complete formulation of kinematics. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. Displacement, velocity and acceleration can be expressed as functions of time. Example 3.1.1 velocity as derivative of position. The first derivative of position is velocity, and the second derivative. Differential Velocity Calculus.
From mavink.com
Average Velocity Equation Differential Velocity Calculus If we express these quantities as functions, they can be related by derivatives. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. Connection at the center of differential calculus. Example 3.1.1 velocity as derivative. Differential Velocity Calculus.
From www.youtube.com
미적분26미분과 거리 속도가속도differential and integral calculusDifferential and Differential Velocity Calculus Integral calculus gives us a more complete formulation of kinematics. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. Chapter 10 velocity, acceleration, and calculus. Example 3.1.1 velocity as derivative of position. The first derivative of position is velocity, and the second derivative is acceleration. If we express. Differential Velocity Calculus.
From www.youtube.com
The total differential Calculus in a Nutshell LetThereBeMath Differential Velocity Calculus If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Integral calculus gives us a more complete formulation of kinematics. If we express these quantities as functions, they can be related by derivatives. Displacement, velocity and acceleration can be expressed as functions of time. 7 rows calculus is. Differential Velocity Calculus.
From mr-mathematics.com
Modelling Motion with Differential Equations Differential Velocity Calculus The first derivative of position is velocity, and the second derivative is acceleration. Integral calculus gives us a more complete formulation of kinematics. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at. Differential Velocity Calculus.
From www.chegg.com
Solved A differential equation for the velocity v of a Differential Velocity Calculus Connection at the center of differential calculus. If we express these quantities as functions, they can be related by derivatives. Integral calculus gives us a more complete formulation of kinematics. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. In this section we look at some applications of. Differential Velocity Calculus.
From www.youtube.com
Velocity Calculus Based Introduction YouTube Differential Velocity Calculus But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. Displacement, velocity and acceleration can be expressed as functions of time. Example 3.1.1 velocity as derivative of position. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). Chapter 10 velocity, acceleration, and calculus. The. Differential Velocity Calculus.
From mathsathome.com
How to Find Displacement, Velocity and Acceleration Differential Velocity Calculus If we express these quantities as functions, they can be related by derivatives. The first derivative of position is velocity, and the second derivative is acceleration. Integral calculus gives us a more complete formulation of kinematics. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). 7 rows calculus is an advanced. Differential Velocity Calculus.
From www.wikihow.com
How to Calculate Average Velocity 12 Steps (with Pictures) Differential Velocity Calculus The first derivative of position is velocity, and the second derivative is acceleration. But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. Chapter 10 velocity, acceleration, and calculus. Integral calculus gives us a more complete formulation of kinematics. In this section we look at some applications of the derivative by focusing on. Differential Velocity Calculus.
From www.youtube.com
Motion along a curve finding velocity magnitude AP Calculus BC Differential Velocity Calculus Connection at the center of differential calculus. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. Example 3.1.1 velocity as derivative of position. Let \(r(t)\). Differential Velocity Calculus.
From www.youtube.com
Interpreting change in speed from velocitytime graph Differential Differential Velocity Calculus If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Chapter 10 velocity, acceleration, and calculus. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). But we cannot predict where dy=dx equals y= x:therefore we now find other ways. Differential Velocity Calculus.
From math.wonderhowto.com
How to Use differential equations to solve for velocity « Math Differential Velocity Calculus Connection at the center of differential calculus. The first derivative of position is velocity, and the second derivative is acceleration. If we express these quantities as functions, they can be related by derivatives. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Integral calculus gives us a. Differential Velocity Calculus.
From www.physicsbootcamp.org
Position, Velocity, Acceleration Summary Differential Velocity Calculus If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Chapter 10 velocity, acceleration, and calculus. Displacement, velocity and acceleration can be expressed as functions of time. The first derivative of position is velocity, and the second derivative is acceleration. Integral calculus gives us a more complete formulation. Differential Velocity Calculus.
From www.ibphysicstutor.net
Topic 2 Differential Velocity Calculus Example 3.1.1 velocity as derivative of position. If we express these quantities as functions, they can be related by derivatives. Chapter 10 velocity, acceleration, and calculus. Integral calculus gives us a more complete formulation of kinematics. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. In this section. Differential Velocity Calculus.
From www.youtube.com
First Equation of Motion Derivation by Calculus Method and Use YouTube Differential Velocity Calculus 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. Displacement, velocity and acceleration can be expressed as functions of time. Integral calculus gives us a more complete formulation of kinematics. But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. Example. Differential Velocity Calculus.
From www.youtube.com
Velocity And Acceleration Solution Differential Equations in Action Differential Velocity Calculus Integral calculus gives us a more complete formulation of kinematics. Connection at the center of differential calculus. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). The first derivative of position is velocity, and the second derivative is acceleration. 7 rows calculus is an advanced math topic,. Differential Velocity Calculus.
From www.chegg.com
Solved Human Terminal velocity is Viņ120 mph using the Differential Velocity Calculus But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate. Differential Velocity Calculus.
From www.youtube.com
Fundamental Theorem of Calculus Using Position and Velocity YouTube Differential Velocity Calculus Example 3.1.1 velocity as derivative of position. But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. If we express these quantities as functions, they can be related by derivatives. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). 7. Differential Velocity Calculus.
From www.youtube.com
Velocity and Acceleration Problems Differential Calculus YouTube Differential Velocity Calculus Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the. Differential Velocity Calculus.
From www.youtube.com
Estimating Velocity Differential Equations in Action YouTube Differential Velocity Calculus In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Connection at the center of differential calculus. Displacement, velocity and acceleration. Differential Velocity Calculus.
From mathsathome.com
How to Find Displacement, Velocity and Acceleration Differential Velocity Calculus Displacement, velocity and acceleration can be expressed as functions of time. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). If we express these quantities as functions, they can be. Differential Velocity Calculus.
From www.youtube.com
Differential Calculus (Feliciano and Uy) Exercise 3.7_Related Rates Differential Velocity Calculus But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. Connection at the center of differential calculus. Integral calculus gives us a more complete formulation of kinematics. If we express these quantities as functions, they can be related by derivatives. Let \(r(t)\) be a differentiable vector valued function representing the position vector of. Differential Velocity Calculus.
From www.tessshebaylo.com
Equation For Velocity Tessshebaylo Differential Velocity Calculus Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). Integral calculus gives us a more complete formulation of kinematics. Chapter 10 velocity, acceleration, and calculus. Example 3.1.1 velocity as derivative of position. Connection at the center of differential calculus. The first derivative of position is velocity, and the second derivative is. Differential Velocity Calculus.
From www.youtube.com
Differential calculus Point moves after 2secs S=2t^2+3t find average Differential Velocity Calculus In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. Chapter 10 velocity, acceleration, and calculus. But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. The first derivative of position is velocity, and the second. Differential Velocity Calculus.
From empoweryourknowledgeandhappytrivia.wordpress.com
Velocity Formula KnowItAll Differential Velocity Calculus 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. If we express these quantities as functions, they can be related by. Differential Velocity Calculus.
From www.coursehero.com
[Solved] Differential Equations Find the velocity at any time t of a 6 Differential Velocity Calculus If we express these quantities as functions, they can be related by derivatives. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. The first derivative of position is velocity, and the second derivative is acceleration. Example 3.1.1 velocity as derivative of position.. Differential Velocity Calculus.
From www.scribd.com
Differential Calculus PDF Maxima And Minima Velocity Differential Velocity Calculus The first derivative of position is velocity, and the second derivative is acceleration. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). Integral calculus gives us a more complete formulation of kinematics. Chapter 10 velocity, acceleration, and calculus. If we express these quantities as functions, they can be related by derivatives.. Differential Velocity Calculus.
From www.slideserve.com
PPT Chapter 6 Differential Calculus PowerPoint Presentation, free Differential Velocity Calculus 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Integral calculus gives us a more complete formulation of kinematics. The first derivative of position is velocity,. Differential Velocity Calculus.
From www.studypool.com
SOLUTION Calculus 1 2 1 the tangent and velocity problem Studypool Differential Velocity Calculus Integral calculus gives us a more complete formulation of kinematics. The first derivative of position is velocity, and the second derivative is acceleration. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). Connection at the center of differential calculus. In this section we look at some applications of the derivative by. Differential Velocity Calculus.
From www.youtube.com
Calculus The Tangent And Velocity Problems YouTube Differential Velocity Calculus But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover a. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). Displacement, velocity and acceleration. Differential Velocity Calculus.
From www.codecademy.com
Differential Calculus Differential Calculus Cheatsheet Codecademy Differential Velocity Calculus If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Integral calculus gives us a more complete formulation of kinematics. Let \(r(t)\) be a differentiable vector valued function representing the position vector of a particle at time \(t\). Connection at the center of differential calculus. Chapter 10 velocity,. Differential Velocity Calculus.
From askfilo.com
ity with Answer in notation of differential calculus, the velocity is Differential Velocity Calculus Example 3.1.1 velocity as derivative of position. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. Chapter 10 velocity, acceleration, and calculus. Integral calculus gives us a more complete formulation of kinematics. But we cannot predict where dy=dx equals y= x:therefore we now find other ways to recover. Differential Velocity Calculus.
From www.slideserve.com
PPT Differential Calculus PowerPoint Presentation, free download ID Differential Velocity Calculus Displacement, velocity and acceleration can be expressed as functions of time. Chapter 10 velocity, acceleration, and calculus. Connection at the center of differential calculus. 7 rows calculus is an advanced math topic, but it makes deriving two of the three equations of motion much simpler. In this section we look at some applications of the derivative by focusing on the. Differential Velocity Calculus.
From www.showme.com
AP CALC Interpreting graphs 4 velocity & acceleration Math, Velocity Differential Velocity Calculus The first derivative of position is velocity, and the second derivative is acceleration. Example 3.1.1 velocity as derivative of position. Displacement, velocity and acceleration can be expressed as functions of time. If acceleration a (t) is known, we can use integral calculus to derive expressions for velocity v (t) and position x (t). Chapter 10 velocity, acceleration, and calculus. In. Differential Velocity Calculus.