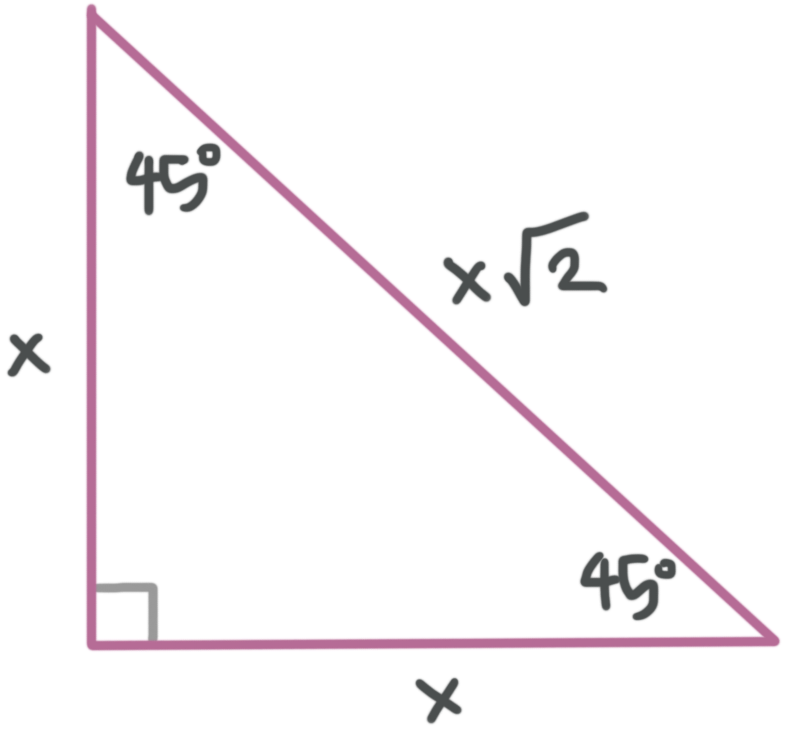
Triangle Special Angles . If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Explains a simple pictorial way to remember basic reference angle values. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of. We can precisely evaluate the trigonometric functions for these special angles without a calculator. Use the special right triangle rations to solve special right triangles. Provides other memory aids for the values of trigonometric ratios for. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Scroll down the page if you need more examples and. Then we will use the pythagorean theorem to find the remaining side length.
from
The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of. The most frequently studied right triangles, the special right triangles, are the 30, 60,. We can precisely evaluate the trigonometric functions for these special angles without a calculator. Use the special right triangle rations to solve special right triangles. Then we will use the pythagorean theorem to find the remaining side length. Scroll down the page if you need more examples and. Provides other memory aids for the values of trigonometric ratios for. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Explains a simple pictorial way to remember basic reference angle values.
Triangle Special Angles The most frequently studied right triangles, the special right triangles, are the 30, 60,. We can precisely evaluate the trigonometric functions for these special angles without a calculator. Use the special right triangle rations to solve special right triangles. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Explains a simple pictorial way to remember basic reference angle values. Provides other memory aids for the values of trigonometric ratios for. Scroll down the page if you need more examples and. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Then we will use the pythagorean theorem to find the remaining side length. The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of.
From
Triangle Special Angles Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Provides other memory aids for the values of trigonometric ratios for. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Scroll down the page if you need more examples and. We can precisely evaluate the trigonometric functions for these special angles. Triangle Special Angles.
From
Triangle Special Angles The most frequently studied right triangles, the special right triangles, are the 30, 60,. The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of. Then we will use the pythagorean theorem to find the remaining side length. Use the special right triangle rations to solve special right. Triangle Special Angles.
From www.vecteezy.com
Special Right Triangle with Angles 30, 60, 90 degrees vintage Triangle Special Angles Use the special right triangle rations to solve special right triangles. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Explains a simple pictorial way to remember basic reference angle values. Scroll down the. Triangle Special Angles.
From
Triangle Special Angles We can precisely evaluate the trigonometric functions for these special angles without a calculator. Use the special right triangle rations to solve special right triangles. Explains a simple pictorial way to remember basic reference angle values. Then we will use the pythagorean theorem to find the remaining side length. The most frequently studied right triangles, the special right triangles, are. Triangle Special Angles.
From
Triangle Special Angles Use the special right triangle rations to solve special right triangles. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Provides other memory aids for the values of trigonometric ratios for. We can precisely evaluate the trigonometric functions for these special. Triangle Special Angles.
From
Triangle Special Angles Then we will use the pythagorean theorem to find the remaining side length. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg. Triangle Special Angles.
From e-gmat.com
Properties of Triangle types & formulas [Video & Practice] Triangle Special Angles Provides other memory aids for the values of trigonometric ratios for. Explains a simple pictorial way to remember basic reference angle values. Scroll down the page if you need more examples and. Use the special right triangle rations to solve special right triangles. We can precisely evaluate the trigonometric functions for these special angles without a calculator. If we are. Triangle Special Angles.
From www.youtube.com
Trigonometry Special triangles YouTube Triangle Special Angles Scroll down the page if you need more examples and. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Use the special right triangle rations to solve special right triangles. Then we will use the pythagorean theorem to find the remaining side length. We can precisely evaluate the trigonometric functions for these special angles without. Triangle Special Angles.
From
Triangle Special Angles Explains a simple pictorial way to remember basic reference angle values. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Provides other memory aids for the values of trigonometric ratios for. The key characteristic of special angles is that their sine,. Triangle Special Angles.
From mathmonks.com
Special Right Triangles Definition, Formula, Examples Triangle Special Angles If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Provides other memory aids for the values of trigonometric ratios for. The key characteristic of special angles is that their sine, cosine, and tangent values. Triangle Special Angles.
From www.varsitytutors.com
Special triangles HiSET Math Triangle Special Angles If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Explains a simple pictorial way to remember basic reference angle values. Then we will use the pythagorean theorem to find the remaining side length. Use. Triangle Special Angles.
From www.alamy.com
The image shows a special triangle rectangle with angles of 45, 45 and Triangle Special Angles Explains a simple pictorial way to remember basic reference angle values. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Provides other memory aids for the values of trigonometric ratios for. The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of. We. Triangle Special Angles.
From
Triangle Special Angles Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Provides other memory aids for the values of trigonometric ratios for. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse).. Triangle Special Angles.
From owlcation.com
A Full Guide to the 306090 Triangle (With Formulas and Examples Triangle Special Angles Scroll down the page if you need more examples and. Provides other memory aids for the values of trigonometric ratios for. The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of. We can precisely evaluate the trigonometric functions for these special angles without a calculator. Use the. Triangle Special Angles.
From
Triangle Special Angles Provides other memory aids for the values of trigonometric ratios for. Then we will use the pythagorean theorem to find the remaining side length. The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of. Scroll down the page if you need more examples and. If we are. Triangle Special Angles.
From calcworkshop.com
Special Right Triangles (Fully Explained w/ 19 Examples!) Triangle Special Angles Explains a simple pictorial way to remember basic reference angle values. Use the special right triangle rations to solve special right triangles. Provides other memory aids for the values of trigonometric ratios for. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. We can precisely evaluate the trigonometric functions for these special angles without a. Triangle Special Angles.
From gogeometry.com
Special Right Triangle 3060, 4545, 3753. Elearning. Triangle Special Angles Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. We can precisely evaluate the trigonometric functions for these special angles without a calculator. Scroll down the page if you need more examples and. Explains a simple pictorial way to remember basic reference angle values. Provides other memory aids for the values of trigonometric ratios for.. Triangle Special Angles.
From matterofmath.com
Special Right Triangles 30 60 90 and 45 45 90 Triangles · Matter of Math Triangle Special Angles Use the special right triangle rations to solve special right triangles. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Provides other memory aids for the values of trigonometric ratios for. Scroll down the. Triangle Special Angles.
From www.tes.com
Geometry Angles in a triangle special cases Year 6 Teaching Resources Triangle Special Angles Use the special right triangle rations to solve special right triangles. Then we will use the pythagorean theorem to find the remaining side length. Explains a simple pictorial way to remember basic reference angle values. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to. Triangle Special Angles.
From mathsux.org
special triangles Archives MathSux^2 Triangle Special Angles Use the special right triangle rations to solve special right triangles. We can precisely evaluate the trigonometric functions for these special angles without a calculator. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots. Triangle Special Angles.
From
Triangle Special Angles Then we will use the pythagorean theorem to find the remaining side length. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Scroll down the page if you need more examples and. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Use the special right triangle rations to solve special. Triangle Special Angles.
From
Triangle Special Angles If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Use the special right triangle rations to solve special right triangles.. Triangle Special Angles.
From
Triangle Special Angles Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Use the special right triangle rations to solve special right triangles. Scroll down the page if you need more examples and. Provides other memory aids for the values of trigonometric ratios for. The key characteristic of special angles is that their sine, cosine, and tangent values. Triangle Special Angles.
From www.youtube.com
Solving triangles with special angles YouTube Triangle Special Angles Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Then we will use the pythagorean theorem to find the remaining side length. Provides other memory aids for the values of trigonometric ratios for. Use the special right triangle rations to solve special right triangles. We can precisely evaluate the trigonometric functions for these special angles. Triangle Special Angles.
From
Triangle Special Angles Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Provides other memory aids for the values of trigonometric ratios for. Explains a simple pictorial way to remember basic reference angle values. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios. Triangle Special Angles.
From
Triangle Special Angles Explains a simple pictorial way to remember basic reference angle values. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). The key characteristic of special angles is that their sine, cosine, and tangent values. Triangle Special Angles.
From mathmonks.com
Isosceles Triangle Definition, Properties, Types, Formulas Triangle Special Angles The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of. We can precisely evaluate the trigonometric functions for these special angles without a calculator. The most frequently studied right triangles, the special right triangles, are the 30, 60,. If we are given a right triangle with one. Triangle Special Angles.
From
Triangle Special Angles Provides other memory aids for the values of trigonometric ratios for. Scroll down the page if you need more examples and. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Trigonometric special angles —. Triangle Special Angles.
From
Triangle Special Angles Explains a simple pictorial way to remember basic reference angle values. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Use the special right triangle rations to solve special right triangles. Provides other memory aids for the values of trigonometric ratios for. If we are given a right triangle with one acute angle and side. Triangle Special Angles.
From
Triangle Special Angles If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). Scroll down the page if you need more examples and. The key characteristic of special angles is that their sine, cosine, and tangent values are. Triangle Special Angles.
From www.youtube.com
454590 Triangles, Special Right Triangle Trigonometry YouTube Triangle Special Angles Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Use the special right triangle rations to solve special right triangles. If we are given a right triangle with one acute angle and side length known, we will first utilize our special. Triangle Special Angles.
From
Triangle Special Angles Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). The key characteristic of special angles is that their sine, cosine,. Triangle Special Angles.
From
Triangle Special Angles We can precisely evaluate the trigonometric functions for these special angles without a calculator. Provides other memory aids for the values of trigonometric ratios for. The key characteristic of special angles is that their sine, cosine, and tangent values are either exact fractions or square roots (surds) of. Scroll down the page if you need more examples and. Explains a. Triangle Special Angles.
From
Triangle Special Angles Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Scroll down the page if you need more examples and. Explains a simple pictorial way to remember basic reference angle values. Provides other memory aids for the values of trigonometric ratios for. The key characteristic of special angles is that their sine, cosine, and tangent values. Triangle Special Angles.
From
Triangle Special Angles Provides other memory aids for the values of trigonometric ratios for. The most frequently studied right triangles, the special right triangles, are the 30, 60,. Trigonometric special angles — 30o, 45o, and 60o — generate rather straightforward trigonometric values. Then we will use the pythagorean theorem to find the remaining side length. The key characteristic of special angles is that. Triangle Special Angles.