Differential Well Defined . A function \ (f\) is differentiable at a point \ (x_0\) if. — a solution to a partial differential equation that is a continuous function of its values on the boundary is. But \(\tfrac{0}{0}\) is not defined. 1) \ (f\) is continuous at \ (x_0\). — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. definitions relating to differentiability.
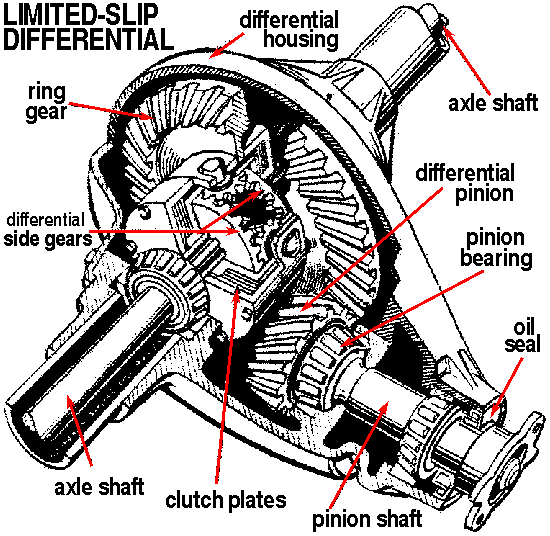
from www.dieselplace.com
— a solution to a partial differential equation that is a continuous function of its values on the boundary is. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. 1) \ (f\) is continuous at \ (x_0\). — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. definitions relating to differentiability. But \(\tfrac{0}{0}\) is not defined. A function \ (f\) is differentiable at a point \ (x_0\) if.
Info Types of differentials explained Diesel Place
Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). definitions relating to differentiability. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). But \(\tfrac{0}{0}\) is not defined. 1) \ (f\) is continuous at \ (x_0\). A function \ (f\) is differentiable at a point \ (x_0\) if. — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. — a solution to a partial differential equation that is a continuous function of its values on the boundary is.
From www.coursehero.com
[Solved] Verify that the given differential equation is exact; then Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). 1) \ (f\) is continuous at \ (x_0\). A function \ (f\) is differentiable at a point \ (x_0\) if. definitions relating to differentiability. — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to. Differential Well Defined.
From www.sodialed.com
differential height definition RC Car Glossary Differential Well Defined — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. definitions relating to differentiability. 1) \ (f\) is continuous at \ (x_0\). furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. — a solution to a partial differential equation. Differential Well Defined.
From www.dieselplace.com
Info Types of differentials explained Diesel Place Differential Well Defined — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. definitions relating to differentiability. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). — a solution to a partial differential equation that is a continuous function of its values on the. Differential Well Defined.
From chemistnotes.com
Differential Thermal AnalysisPrinciple, Detailed Instrumentation, and Differential Well Defined A function \ (f\) is differentiable at a point \ (x_0\) if. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. 1) \ (f\) is continuous at \ (x_0\). But \(\tfrac{0}{0}\) is not. Differential Well Defined.
From www.cuemath.com
Differential Equation Meaning, Types, Order, Degree & Solution Cuemath Differential Well Defined A function \ (f\) is differentiable at a point \ (x_0\) if. — a solution to a partial differential equation that is a continuous function of its values on the boundary is. — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. furthermore, if a function of one variable is differentiable at a. Differential Well Defined.
From medium.com
Differential Equations Data Analysis Center Medium Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). A function \ (f\) is differentiable at a point \ (x_0\) if. definitions relating to differentiability. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no. Differential Well Defined.
From www.theengineeringprojects.com
Differential Analysis of Fluid Flow The Engineering Projects Differential Well Defined — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. — a solution to a partial differential equation that is a continuous function of its values on the boundary is. A function \ (f\) is differentiable at a point \ (x_0\) if. — the differential of x, denoted dx , is any nonzero. Differential Well Defined.
From www.youtube.com
🔵02 Order and Degree of a Differential Equation Exercise YouTube Differential Well Defined — a solution to a partial differential equation that is a continuous function of its values on the boundary is. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. A function \. Differential Well Defined.
From www.slideserve.com
PPT Differential Leveling PowerPoint Presentation, free download ID Differential Well Defined But \(\tfrac{0}{0}\) is not defined. — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. definitions relating to differentiability. — a solution to a partial differential equation that is a continuous function of its values on the boundary is. furthermore, if a function of one variable is differentiable at a point, the. Differential Well Defined.
From electrical-engineering-portal.com
Four Special Differential Protections And Their Respective CT Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. 1) \ (f\) is continuous at \ (x_0\). — as \(x\) tends to \(a\text{,}\) the. Differential Well Defined.
From www.testandmeasurementtips.com
Sorting out balanced cables and differential signaling Differential Well Defined 1) \ (f\) is continuous at \ (x_0\). A function \ (f\) is differentiable at a point \ (x_0\) if. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. definitions. Differential Well Defined.
From www.dieselplace.com
Info Types of differentials explained Diesel Place Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). But \(\tfrac{0}{0}\) is not defined. — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. — a solution to a partial differential equation that is a continuous function of its values on the. Differential Well Defined.
From studylib.net
Chapter 2 Systems Defined by Differential or Difference Equations Differential Well Defined — a solution to a partial differential equation that is a continuous function of its values on the boundary is. definitions relating to differentiability. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). 1) \ (f\) is continuous at \ (x_0\). — as \(x\) tends. Differential Well Defined.
From nearsay.com
What Is a Differential? New York Transmission Service Ontario NearSay Differential Well Defined — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. 1) \ (f\) is continuous at \ (x_0\). definitions relating to differentiability. A function \ (f\) is differentiable at a point \ (x_0\) if. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small. Differential Well Defined.
From www.researchgate.net
Examples of how the differential acts. The differential is defined by Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). — a solution to a partial differential equation that is a continuous function of its values on the boundary is. A function \ (f\) is differentiable at a point \ (x_0\) if. furthermore, if a function of. Differential Well Defined.
From www.cuemath.com
Differential Calculus Terms, Formulas, Rules, Examples Differential Well Defined — a solution to a partial differential equation that is a continuous function of its values on the boundary is. 1) \ (f\) is continuous at \ (x_0\). But \(\tfrac{0}{0}\) is not defined. definitions relating to differentiability. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number).. Differential Well Defined.
From www.researchgate.net
Differential growth shapes. (a) Examples of folding geometries that Differential Well Defined 1) \ (f\) is continuous at \ (x_0\). — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. definitions relating to differentiability. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). A function \ (f\) is differentiable at a point \ (x_0\). Differential Well Defined.
From www.slideserve.com
PPT Differential Diagnoses PowerPoint Presentation, free download Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). A function \ (f\) is differentiable at a point \ (x_0\) if. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. definitions relating to. Differential Well Defined.
From www.mrclutchnw.com
Differential Rebuilding Mr. Clutch Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). definitions relating to differentiability. But \(\tfrac{0}{0}\) is not defined. A function \ (f\) is differentiable at a point \ (x_0\) if. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth”. Differential Well Defined.
From www.pinterest.co.uk
Types of Differentials and How They Work? Automotive engineering, Car Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). — a solution to a partial differential equation that is a continuous function of its values on the boundary is. A function \ (f\) is differentiable at a point \ (x_0\) if. — as \(x\) tends to. Differential Well Defined.
From www.carexpert.com.au
Differentials explained CarExpert Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). A function \ (f\) is differentiable at a point \ (x_0\) if. — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. But \(\tfrac{0}{0}\) is not defined. furthermore, if a function of one. Differential Well Defined.
From www.youtube.com
How A DIfferential Works Differential Animation X Engineering YouTube Differential Well Defined 1) \ (f\) is continuous at \ (x_0\). — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. A function \ (f\) is differentiable at a point \ (x_0\) if. But \(\tfrac{0}{0}\). Differential Well Defined.
From www.researchgate.net
(PDF) Differential equations defined on algebraic curves Differential Well Defined A function \ (f\) is differentiable at a point \ (x_0\) if. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). definitions relating to differentiability. 1) \ (f\) is continuous at \ (x_0\). But \(\tfrac{0}{0}\) is not defined. — a solution to a partial differential equation. Differential Well Defined.
From www.researchgate.net
(PDF) WellDefined Solvability of Some DifferentialDifference Differential Well Defined 1) \ (f\) is continuous at \ (x_0\). — a solution to a partial differential equation that is a continuous function of its values on the boundary is. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. — as \(x\) tends to \(a\text{,}\) the. Differential Well Defined.
From www.youtube.com
Differential Geometry Lecture 15 part 1 Shape Operator Defined YouTube Differential Well Defined A function \ (f\) is differentiable at a point \ (x_0\) if. — a solution to a partial differential equation that is a continuous function of its values on the boundary is. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. definitions relating to. Differential Well Defined.
From e2e.ti.com
Differential pairs what you really need to know Analog Technical Differential Well Defined — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). — a solution to a partial differential equation that is a continuous function of its values on the boundary is. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at. Differential Well Defined.
From www.researchgate.net
Differential capacity dí µí± ∕dí µí± as well as differential pressure Differential Well Defined definitions relating to differentiability. But \(\tfrac{0}{0}\) is not defined. 1) \ (f\) is continuous at \ (x_0\). — a solution to a partial differential equation that is a continuous function of its values on the boundary is. A function \ (f\) is differentiable at a point \ (x_0\) if. furthermore, if a function of one variable is. Differential Well Defined.
From schools.studyrate.in
Differential calculus Defined and explained with examples Study Rate Differential Well Defined definitions relating to differentiability. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. 1) \ (f\) is continuous at \ (x_0\). — as. Differential Well Defined.
From www.mech4study.com
Differential Gear Working mech4study Differential Well Defined 1) \ (f\) is continuous at \ (x_0\). — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). definitions relating to differentiability. — a solution to a partial differential equation that is. Differential Well Defined.
From www.researchgate.net
Differential diagnosis of a welldefined radiolucent bone image Differential Well Defined — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. — a solution to a partial differential equation that is a continuous function of its values on the boundary is. . Differential Well Defined.
From thereviewstories.com
What is Differential Types of Differential Locking & Open Differential Differential Well Defined — a solution to a partial differential equation that is a continuous function of its values on the boundary is. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). 1) \ (f\) is continuous at \ (x_0\). A function \ (f\) is differentiable at a point \. Differential Well Defined.
From www.slideserve.com
PPT Differential Leveling PowerPoint Presentation ID3215747 Differential Well Defined — as \(x\) tends to \(a\text{,}\) the numerator and denominator both tend to zero. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). — a solution to a partial differential equation that is a continuous function of its values on the boundary is. A function \. Differential Well Defined.
From www.researchgate.net
Fig. S6. The differential stability gradient is conserved in clusters Differential Well Defined — a solution to a partial differential equation that is a continuous function of its values on the boundary is. definitions relating to differentiability. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small number). furthermore, if a function of one variable is differentiable at a point,. Differential Well Defined.
From innovationdiscoveries.space
DIFFERENTIAL FUNCTIONS WORKING PRINCIPLES AND CLASSIFICATION Differential Well Defined furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. definitions relating to differentiability. A function \ (f\) is differentiable at a point \ (x_0\) if. — the differential of x, denoted dx , is any nonzero real number (usually taken to be a small. Differential Well Defined.
From www.drillingformulas.com
Differential Sticking Causes Stuck Pipe Drilling Formulas and Differential Well Defined 1) \ (f\) is continuous at \ (x_0\). But \(\tfrac{0}{0}\) is not defined. furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners. A function \ (f\) is differentiable at a point \ (x_0\) if. — as \(x\) tends to \(a\text{,}\) the numerator and denominator both. Differential Well Defined.