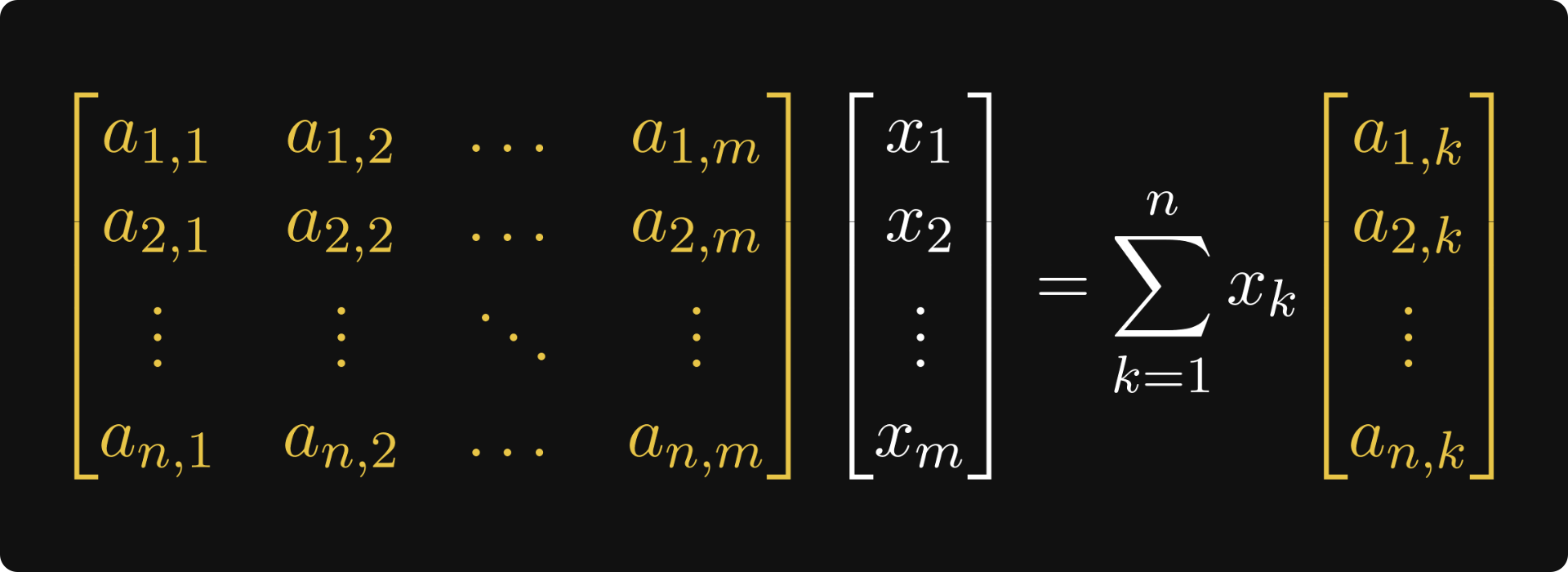
Julia Matrix Vector Multiplication . Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. One of the friendliest problems for vectorization is matrix multiplication. Vector) @boundscheck size (a, 2) == length (x) || throw. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. Specifically, i want to evaluate the. As we can see, julia found. In front of the operator or function call to indicate you want elementwise multiplication and not an. We can allocate a vector by typing:
from thepalindrome.org
Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. We can allocate a vector by typing: One of the friendliest problems for vectorization is matrix multiplication. Specifically, i want to evaluate the. As we can see, julia found. In front of the operator or function call to indicate you want elementwise multiplication and not an. Vector) @boundscheck size (a, 2) == length (x) || throw. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing.
Epsilons, no. 2 Understanding matrix multiplication
Julia Matrix Vector Multiplication Vector) @boundscheck size (a, 2) == length (x) || throw. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. As we can see, julia found. In front of the operator or function call to indicate you want elementwise multiplication and not an. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. We can allocate a vector by typing: Vector) @boundscheck size (a, 2) == length (x) || throw. Specifically, i want to evaluate the. One of the friendliest problems for vectorization is matrix multiplication.
From nicmens.weebly.com
Matrix by vector multiplication matlab nicmens Julia Matrix Vector Multiplication Specifically, i want to evaluate the. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. One of the friendliest problems for vectorization is matrix multiplication. As we can see, julia found. We can allocate a vector by typing: In front of the operator or function call to indicate you want elementwise multiplication. Julia Matrix Vector Multiplication.
From rumble.com
Matrix Multiplication Julia Matrix Vector Multiplication As we can see, julia found. We can allocate a vector by typing: Vector) @boundscheck size (a, 2) == length (x) || throw. One of the friendliest problems for vectorization is matrix multiplication. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. In front of the operator. Julia Matrix Vector Multiplication.
From www.chegg.com
Consider a parallel matrix vector multiplication Julia Matrix Vector Multiplication Specifically, i want to evaluate the. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. One of the friendliest problems for vectorization is matrix multiplication. In front of the operator or function call to indicate you want elementwise multiplication and not an. Vector) @boundscheck size (a, 2) == length (x) || throw. We can allocate a vector by typing: As we can see, julia. Julia Matrix Vector Multiplication.
From www.youtube.com
Matrixvector and Matrixmatrix Multiplication YouTube Julia Matrix Vector Multiplication Vector) @boundscheck size (a, 2) == length (x) || throw. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. One of the friendliest problems for vectorization is matrix multiplication. In front of the operator or function call to indicate you want elementwise multiplication and not an. As. Julia Matrix Vector Multiplication.
From blog.csdn.net
Matrix in Julia (Julia ไธญ็็ฉ้ต๏ผCSDNๅๅฎข Julia Matrix Vector Multiplication Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. We can allocate a vector by typing: Specifically, i want to evaluate the. As we can see, julia found. In front of the operator or function call to indicate you want elementwise multiplication and not an. Vector) @boundscheck size (a, 2) == length (x) || throw. Multiplication with the identity operator i is a noop. Julia Matrix Vector Multiplication.
From ninamclean.weebly.com
Matrix multiplication Nina McLean Julia Matrix Vector Multiplication One of the friendliest problems for vectorization is matrix multiplication. In front of the operator or function call to indicate you want elementwise multiplication and not an. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. Given m ร k matrix ๐, and k ร n. Julia Matrix Vector Multiplication.
From www.slideserve.com
PPT Systolic Arrays MatrixVector Multiplication PowerPoint Julia Matrix Vector Multiplication Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. In front of the operator or function call to indicate you want elementwise multiplication and not an. Vector) @boundscheck size (a, 2) == length (x) || throw. As we can see, julia found. Given m ร k. Julia Matrix Vector Multiplication.
From www.chegg.com
Solved 2.2 MatrixVector Multiplication Problem 10 (1 Julia Matrix Vector Multiplication Vector) @boundscheck size (a, 2) == length (x) || throw. One of the friendliest problems for vectorization is matrix multiplication. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. In front of the operator or function call to indicate you want elementwise multiplication and not an. Multiplication. Julia Matrix Vector Multiplication.
From digitalsystemdesign.in
ScalarVector Multiplication Digital System Design Julia Matrix Vector Multiplication Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. One of the friendliest problems for vectorization is matrix multiplication. Vector) @boundscheck size (a, 2) == length (x) || throw. We can allocate a vector by typing: Multiplication with the identity operator i is a noop (except for. Julia Matrix Vector Multiplication.
From www.chegg.com
Question 12 Matrix Vector Multiplication Given Julia Matrix Vector Multiplication Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Vector) @boundscheck size (a, 2) == length (x) || throw. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. As we can see, julia. Julia Matrix Vector Multiplication.
From blog.csdn.net
Matrix in Julia (Julia ไธญ็็ฉ้ต๏ผCSDNๅๅฎข Julia Matrix Vector Multiplication Specifically, i want to evaluate the. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. As we can see, julia found. In front of. Julia Matrix Vector Multiplication.
From github.com
Could sparse matrixvector multiplication be optimized ยท Issue 35829 Julia Matrix Vector Multiplication Vector) @boundscheck size (a, 2) == length (x) || throw. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. One of the friendliest problems for vectorization is matrix multiplication. As we can see, julia found. In front of the operator or function call to indicate you. Julia Matrix Vector Multiplication.
From ccssmathanswers.com
Multiplication of Two Matrices Definition, Formula, Properties Julia Matrix Vector Multiplication As we can see, julia found. We can allocate a vector by typing: One of the friendliest problems for vectorization is matrix multiplication. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Specifically, i want to evaluate the. Vector) @boundscheck size (a, 2) == length (x) || throw. In front of the operator or function call to indicate you want elementwise multiplication and not. Julia Matrix Vector Multiplication.
From www.chegg.com
Solved Matrix/Vector Multiplication A matrix, A, can be Julia Matrix Vector Multiplication In front of the operator or function call to indicate you want elementwise multiplication and not an. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. We can allocate a vector by typing: Vector) @boundscheck size (a, 2) == length (x) || throw. As we can. Julia Matrix Vector Multiplication.
From www.youtube.com
Matrix Vector Multiplication by MapReduce Hadoop HDFS and MapReduce Julia Matrix Vector Multiplication Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. Specifically, i want to evaluate the. Vector) @boundscheck size (a, 2) == length (x) || throw. We can allocate a vector by typing: As we can see, julia found. In front of the operator or function call to indicate you want elementwise multiplication. Julia Matrix Vector Multiplication.
From mbernste.github.io
Matrixvector multiplication Matthew N. Bernstein Julia Matrix Vector Multiplication Specifically, i want to evaluate the. One of the friendliest problems for vectorization is matrix multiplication. In front of the operator or function call to indicate you want elementwise multiplication and not an. We can allocate a vector by typing: Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. Function jgemvavx!(๐ฒ, ๐,. Julia Matrix Vector Multiplication.
From debmoran.blogspot.com
Matrix Vector Multiplication Mapreduce Example Deb Moran's Julia Matrix Vector Multiplication Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. We can allocate a vector by typing: As we can see, julia found. One of the friendliest problems for vectorization is matrix multiplication. Specifically, i want to evaluate the. Given m ร k matrix ๐, and k. Julia Matrix Vector Multiplication.
From vimsky.com
Julia vec()็จๆณๅไปฃ็ ็คบไพ ็บฏๅๅคฉ็ฉบ Julia Matrix Vector Multiplication Vector) @boundscheck size (a, 2) == length (x) || throw. As we can see, julia found. In front of the operator or function call to indicate you want elementwise multiplication and not an. One of the friendliest problems for vectorization is matrix multiplication. We can allocate a vector by typing: Specifically, i want to evaluate the. Function jgemvavx!(๐ฒ, ๐, ๐ฑ). Julia Matrix Vector Multiplication.
From blog.csdn.net
Matrix in Julia (Julia ไธญ็็ฉ้ต๏ผCSDNๅๅฎข Julia Matrix Vector Multiplication Vector) @boundscheck size (a, 2) == length (x) || throw. In front of the operator or function call to indicate you want elementwise multiplication and not an. Specifically, i want to evaluate the. One of the friendliest problems for vectorization is matrix multiplication. As we can see, julia found. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Given m ร k matrix ๐,. Julia Matrix Vector Multiplication.
From www.youtube.com
Math and Dynamics Vector Cross Product as MatrixVector Multiplication Julia Matrix Vector Multiplication We can allocate a vector by typing: One of the friendliest problems for vectorization is matrix multiplication. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. In front of the operator or function call to indicate you want elementwise multiplication and not an. Vector) @boundscheck size (a, 2) == length (x) || throw. As we can see, julia found. Given m ร k matrix. Julia Matrix Vector Multiplication.
From www.youtube.com
Matrix Vector Multiplication YouTube Julia Matrix Vector Multiplication In front of the operator or function call to indicate you want elementwise multiplication and not an. Specifically, i want to evaluate the. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. One of the friendliest problems for vectorization is matrix multiplication. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. Vector) @boundscheck size (a, 2). Julia Matrix Vector Multiplication.
From www.slideserve.com
PPT MATRIX ALGEBRA PowerPoint Presentation, free download ID4712121 Julia Matrix Vector Multiplication One of the friendliest problems for vectorization is matrix multiplication. We can allocate a vector by typing: In front of the operator or function call to indicate you want elementwise multiplication and not an. Specifically, i want to evaluate the. As we can see, julia found. Vector) @boundscheck size (a, 2) == length (x) || throw. Function jgemvavx!(๐ฒ, ๐, ๐ฑ). Julia Matrix Vector Multiplication.
From en.rattibha.com
Linear algebra's most important operations 1๏ธโฃ Vectorvector Julia Matrix Vector Multiplication Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. Vector) @boundscheck size (a, 2) == length (x) || throw. We can allocate a vector by typing: Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. One of the. Julia Matrix Vector Multiplication.
From www.geeksforgeeks.org
NumPy Vector Multiplication Julia Matrix Vector Multiplication Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. One of the friendliest problems for vectorization is matrix multiplication. As we can see, julia found. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. In front of the operator or function call to indicate you want elementwise multiplication and not an. Vector) @boundscheck size (a, 2). Julia Matrix Vector Multiplication.
From www.slideserve.com
PPT Systolic Arrays MatrixVector Multiplication PowerPoint Julia Matrix Vector Multiplication We can allocate a vector by typing: Specifically, i want to evaluate the. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. In front of the operator or function call to indicate you want elementwise multiplication and not an. As we can see, julia found. Vector). Julia Matrix Vector Multiplication.
From medium.com
Sparse Matrix Multiplication. Description by Glyn Liu Medium Julia Matrix Vector Multiplication Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Vector) @boundscheck size (a, 2) == length (x) || throw. In front of the operator or function call to indicate you want elementwise multiplication and not an. One of the friendliest problems for vectorization is matrix multiplication. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. As. Julia Matrix Vector Multiplication.
From mbernste.github.io
Matrixvector multiplication Matthew N. Bernstein Julia Matrix Vector Multiplication Specifically, i want to evaluate the. As we can see, julia found. One of the friendliest problems for vectorization is matrix multiplication. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. In front of the operator or function call to indicate. Julia Matrix Vector Multiplication.
From thepalindrome.org
Epsilons, no. 2 Understanding matrix multiplication Julia Matrix Vector Multiplication Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. We can allocate a vector by typing: One of the friendliest problems for vectorization is matrix multiplication. Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. As we can see, julia found. Given m ร k matrix ๐, and k ร. Julia Matrix Vector Multiplication.
From www.slideserve.com
PPT Refresher Vector and Matrix Algebra PowerPoint Presentation ID Julia Matrix Vector Multiplication Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. One of the friendliest problems for vectorization is matrix multiplication. Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. Specifically, i want to evaluate the. We can allocate a vector by typing: As we can see, julia found. Multiplication with the identity operator i is a noop. Julia Matrix Vector Multiplication.
From tivadardanka.com
What's behind matrix multiplication? Mathematics of machine learning Julia Matrix Vector Multiplication Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. We can allocate a vector by typing: Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. As we can see, julia found. In front of the operator or function call to indicate you want elementwise multiplication and not an. Multiplication with the identity operator i is a. Julia Matrix Vector Multiplication.
From chem.libretexts.org
15.3 Matrix Multiplication Chemistry LibreTexts Julia Matrix Vector Multiplication Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Vector) @boundscheck size (a, 2) == length (x) || throw. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. In front of the operator or function call to indicate you want elementwise multiplication and not an. Given m ร k matrix. Julia Matrix Vector Multiplication.
From blog.csdn.net
Matrix in Julia (Julia ไธญ็็ฉ้ต๏ผCSDNๅๅฎข Julia Matrix Vector Multiplication As we can see, julia found. One of the friendliest problems for vectorization is matrix multiplication. Vector) @boundscheck size (a, 2) == length (x) || throw. We can allocate a vector by typing: Function jgemvavx!(๐ฒ, ๐, ๐ฑ) @avx. Specifically, i want to evaluate the. In front of the operator or function call to indicate you want elementwise multiplication and not. Julia Matrix Vector Multiplication.
From blog.csdn.net
Matrix in Julia (Julia ไธญ็็ฉ้ต๏ผCSDNๅๅฎข Julia Matrix Vector Multiplication Vector) @boundscheck size (a, 2) == length (x) || throw. As we can see, julia found. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. We can allocate a vector by typing: Specifically, i want to evaluate the. In front of the operator or function call. Julia Matrix Vector Multiplication.
From www.youtube.com
Matrix Multiplication YouTube Julia Matrix Vector Multiplication As we can see, julia found. In front of the operator or function call to indicate you want elementwise multiplication and not an. One of the friendliest problems for vectorization is matrix multiplication. Specifically, i want to evaluate the. Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost. Julia Matrix Vector Multiplication.
From thepalindrome.org
Epsilons, no. 2 Understanding matrix multiplication Julia Matrix Vector Multiplication Multiplication with the identity operator i is a noop (except for checking that the scaling factor is one) and therefore almost without overhead. As we can see, julia found. We can allocate a vector by typing: Given m ร k matrix ๐, and k ร n matrix ๐, multiplying them is like performing. One of the friendliest problems for vectorization. Julia Matrix Vector Multiplication.
