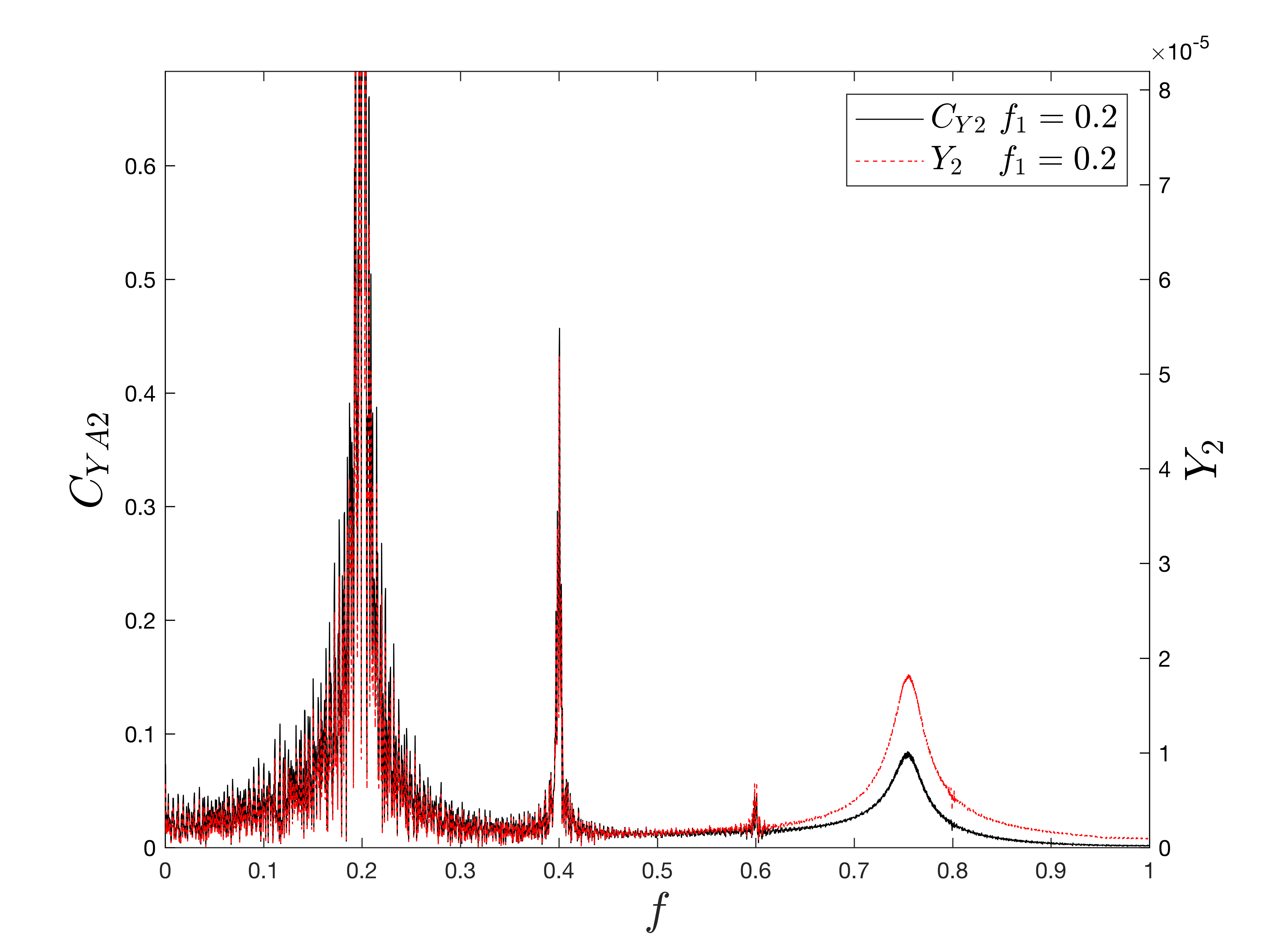
Use Of Fft In Signal Processing . The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm.
from dsp.stackexchange.com
We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform.
resonance How to understand multiple peaks in FFT analysis? Signal
Use Of Fft In Signal Processing In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform.
From dsp.stackexchange.com
python scipy fft on numpy hanning window smears peaks Signal Use Of Fft In Signal Processing The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. We will first discuss deriving the actual fft algorithm, some of its implications for the. Use Of Fft In Signal Processing.
From www.exploremetakinetic.com
FFT, but why? Meta Innovative AI Analytics and Training Software Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). We will first discuss deriving the actual fft algorithm, some of its implications for the. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
Zero Padding in FFT Signal Processing Stack Exchange Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried. Use Of Fft In Signal Processing.
From www.youtube.com
How the 2D FFT works Signal Processing Tutorial YouTube Use Of Fft In Signal Processing The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. In 1965, ibm researcher jim cooley and princeton. Use Of Fft In Signal Processing.
From www.ezlsoftware.com
Signal Processing Toolset™ FFT iFFT EZL Software Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. In 1965, ibm researcher jim cooley and princeton faculty. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
fourier transform Artifacts in FFT Signal Processing Stack Exchange Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). The fast fourier transform (fft) is an efficient. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
filters Remove Noise from Physiological Signals Signal Processing Use Of Fft In Signal Processing The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. In 1965, ibm researcher jim cooley and princeton. Use Of Fft In Signal Processing.
From biomedicalsignalandimage.blogspot.com
Biomedical Signal and Image Processing projects using Matlab and Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is. Use Of Fft In Signal Processing.
From terpconnect.umd.edu
Intro. to Signal ProcessingFourier filter Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft). Use Of Fft In Signal Processing.
From www.pinterest.com
Chirp Signal Frequency Sweeping FFT and power spectral density Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. In 1965, ibm researcher jim cooley and princeton faculty. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
fft Intuition for how a Fourier transform handles signals where the Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. In 1965, ibm researcher jim cooley and princeton. Use Of Fft In Signal Processing.
From www.semanticscholar.org
[PDF] Exact Signal Measurements using FFT Analysis Semantic Scholar Use Of Fft In Signal Processing In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. The fast fourier transform (fft) is an efficient. Use Of Fft In Signal Processing.
From terpconnect.umd.edu
Intro. to Signal ProcessingFourier filter Use Of Fft In Signal Processing The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. In 1965, ibm researcher jim cooley and princeton. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
resonance How to understand multiple peaks in FFT analysis? Signal Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft). Use Of Fft In Signal Processing.
From stackoverflow.com
python How to identify local maxima of FFT data Stack Overflow Use Of Fft In Signal Processing In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. The fast fourier transform (fft) is an efficient. Use Of Fft In Signal Processing.
From www.congress-intercultural.eu
Guide To FFT Analysis (Fast Fourier Transform) Dewesoft, 60 OFF Use Of Fft In Signal Processing In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. Find the frequency components of a signal buried. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
matlab Need help with FFT results Signal Processing Stack Exchange Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. We will first discuss deriving the actual fft algorithm, some of its implications for the. Use Of Fft In Signal Processing.
From makersportal.com
Audio Processing in Python Part I Sampling, Nyquist, and the Fast Use Of Fft In Signal Processing The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is. Use Of Fft In Signal Processing.
From sites.northwestern.edu
Developing An Intuition for Fourier Transforms Elan NessCohn Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. The fast fourier transform (fft) is an efficient computation. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
fft Complex impulse response functions? Signal Processing Stack Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is. Use Of Fft In Signal Processing.
From qingkaikong.blogspot.com
Qingkai's Blog Signal processing FFT with different level of noise Use Of Fft In Signal Processing The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is. Use Of Fft In Signal Processing.
From sapienlabs.org
Factors that Impact Power Spectral Density Estimation Sapien Labs Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried. Use Of Fft In Signal Processing.
From www.ezlsoftware.com
fft_signal_processing EZL Software Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft). Use Of Fft In Signal Processing.
From laptrinhx.com
Audio Analysis With Machine Learning Building AIFueled Sound Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. In 1965, ibm researcher jim cooley and princeton faculty. Use Of Fft In Signal Processing.
From www.researchgate.net
Corresponding FFT for the signal of Figure 2 Download Scientific Diagram Use Of Fft In Signal Processing In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. Find the frequency components of a signal buried. Use Of Fft In Signal Processing.
From github.com
GitHub KRprojecttech/FFT_filter MATLAB code for Low Pass Filter Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). Find the frequency components of a signal buried. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
matlab Deconvolve using divsion of FFT of shifted signal in time Use Of Fft In Signal Processing In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. We will first discuss deriving the actual fft algorithm, some of its implications for the. Use Of Fft In Signal Processing.
From realpython.com
Fourier Transforms With scipy.fft Python Signal Processing Real Python Use Of Fft In Signal Processing In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. We will first discuss deriving the actual fft algorithm, some of its implications for the. Use Of Fft In Signal Processing.
From www.youtube.com
DSP46 problem on 4 point DFT using DIF FFT in digital signal Use Of Fft In Signal Processing In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft). Use Of Fft In Signal Processing.
From kienitvc.ac.ke
signal analysis Interpreting the FFT results of a structural Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried. Use Of Fft In Signal Processing.
From www.researchgate.net
a) FFT spectrum of the signal presented in Fig. 4, b) FFT spectrum of Use Of Fft In Signal Processing The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. We will first discuss deriving the actual fft algorithm, some of its implications for the. Use Of Fft In Signal Processing.
From github.com
fftalgorithm · GitHub Topics · GitHub Use Of Fft In Signal Processing In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is now known as the fast fourier transform (fft). The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. We will first discuss deriving the actual fft algorithm, some of its implications for. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
frequency folding due to aliasing in FFT Signal Processing Stack Exchange Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. In 1965, ibm researcher jim cooley and princeton. Use Of Fft In Signal Processing.
From www.eenewsautomotive.com
An Efficient and Safe Approach of Radar Signal Capturing and Processing Use Of Fft In Signal Processing We will first discuss deriving the actual fft algorithm, some of its implications for the dft, and a speed comparison to drive home the importance of this powerful algorithm. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. Find the frequency components of a signal buried. Use Of Fft In Signal Processing.
From dsp.stackexchange.com
1D convolution and deconvolution using FFT Signal Processing Stack Use Of Fft In Signal Processing Find the frequency components of a signal buried in noise and find the amplitudes of the peak frequencies by using fourier transform. The fast fourier transform (fft) is an efficient computation of the discrete fourier transform (dft) and one of the most important tools used. In 1965, ibm researcher jim cooley and princeton faculty member john tukey developed what is. Use Of Fft In Signal Processing.