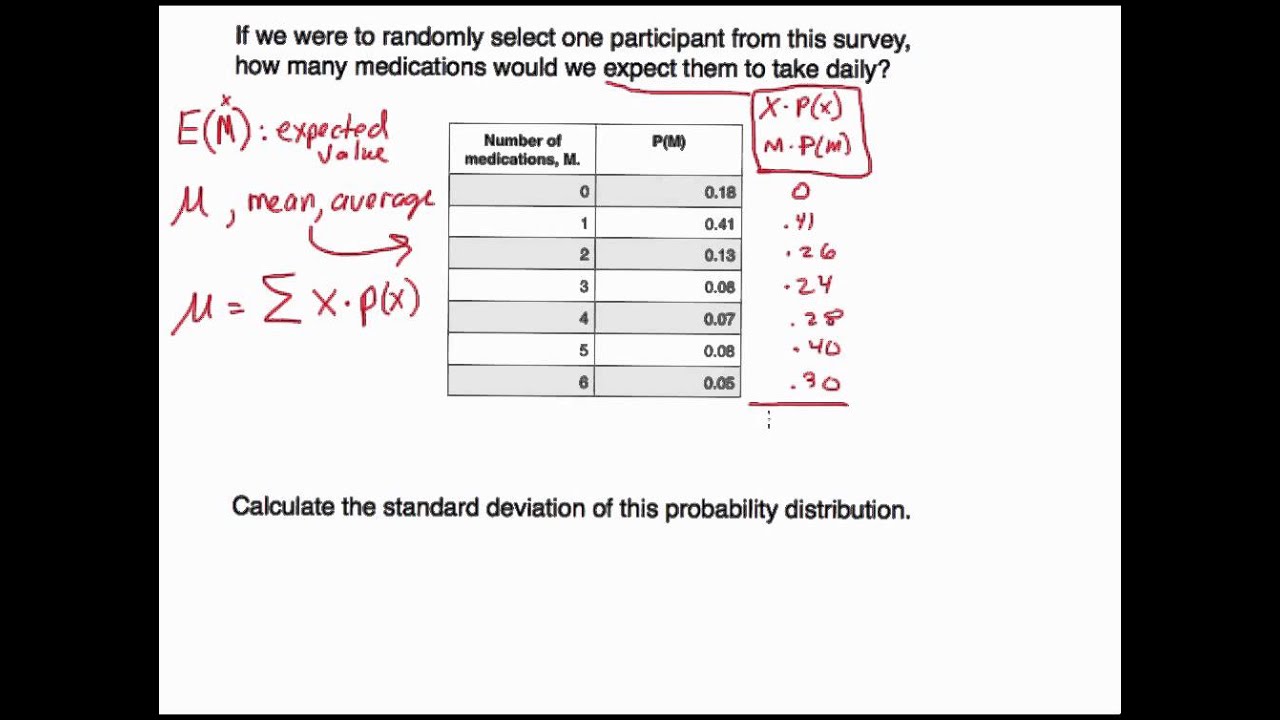
Find The Standard Deviation Of The Random Variable With The Following Probability Distribution . Variance (σ 2) = 0.9475. There are four steps to finding the standard deviation of random variables. This calculator finds mean, standard deviation and variance of a distribution. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: The calculator will generate a step by step explanation along with. First, calculate the mean of the random variables. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: Standard deviation (σ) = 0.9734. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its.
from www.youtube.com
Variance (σ 2) = 0.9475. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. There are four steps to finding the standard deviation of random variables. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: The calculator will generate a step by step explanation along with. First, calculate the mean of the random variables. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: This calculator finds mean, standard deviation and variance of a distribution. Standard deviation (σ) = 0.9734.
Discrete Probability Distributions Finding Probabilities, Expected
Find The Standard Deviation Of The Random Variable With The Following Probability Distribution There are four steps to finding the standard deviation of random variables. First, calculate the mean of the random variables. Variance (σ 2) = 0.9475. The calculator will generate a step by step explanation along with. Standard deviation (σ) = 0.9734. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. This calculator finds mean, standard deviation and variance of a distribution. There are four steps to finding the standard deviation of random variables. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation:
From saylordotorg.github.io
Continuous Random Variables Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Standard deviation (σ) = 0.9734. The calculator will generate a step by step explanation along with. Variance (σ 2) = 0.9475. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: First, calculate the mean of the random variables. To find the variance σ 2 σ 2 of a discrete probability. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.youtube.com
Computing the Mean, Variance and Standard Deviation of a Discrete Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Variance (σ 2) = 0.9475. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: Standard deviation (σ) = 0.9734. There are four steps to finding the standard deviation of random variables. The calculator will generate a step by step explanation along with. We can use the following process to find. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.youtube.com
Variance and Standard Deviation of Discrete Random Variables YouTube Find The Standard Deviation Of The Random Variable With The Following Probability Distribution The calculator will generate a step by step explanation along with. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. First, calculate the mean. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From socratic.org
X is a normally distributed random variable with a mean of 22 and a Find The Standard Deviation Of The Random Variable With The Following Probability Distribution First, calculate the mean of the random variables. This calculator finds mean, standard deviation and variance of a distribution. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\),. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From teachoo.com
Example 10 Calculate mean, variance, standard deviation Find The Standard Deviation Of The Random Variable With The Following Probability Distribution This calculator finds mean, standard deviation and variance of a distribution. The calculator will generate a step by step explanation along with. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: Standard deviation (σ) = 0.9734. To find the variance σ 2 σ 2 of a discrete probability distribution, find. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.nagwa.com
Question Video Calculating the Standard Deviation of a Discrete Random Find The Standard Deviation Of The Random Variable With The Following Probability Distribution To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. This calculator finds mean, standard deviation and variance of a distribution. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.slideserve.com
PPT Discrete Random Variables PowerPoint Presentation ID1718497 Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Standard deviation (σ) = 0.9734. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: To find the variance σ 2 σ 2. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.chegg.com
Solved Assume the random variable X is normally distributed, Find The Standard Deviation Of The Random Variable With The Following Probability Distribution This calculator finds mean, standard deviation and variance of a distribution. Standard deviation (σ) = 0.9734. The calculator will generate a step by step explanation along with. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: There are four steps to. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.chegg.com
Solved Compute the mean and standard deviation of the random Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Variance (σ 2) = 0.9475. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: The calculator will generate a step by step explanation along with. Standard deviation (σ) = 0.9734. There are four steps to finding the standard deviation of random. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.slideserve.com
PPT Chapter 8 Random Variables PowerPoint Presentation, free download Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Standard deviation (σ) = 0.9734. This calculator finds mean, standard deviation and variance of a distribution. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: There are four steps to finding the standard deviation of random variables. First, calculate the mean of the random variables. The calculator will generate a. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.youtube.com
Discrete Probability Distributions Finding Probabilities, Expected Find The Standard Deviation Of The Random Variable With The Following Probability Distribution This calculator finds mean, standard deviation and variance of a distribution. First, calculate the mean of the random variables. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: Variance (σ 2) = 0.9475. There are four steps to finding the standard. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.teachoo.com
Question 8 A random variable X has probability distribution Find The Standard Deviation Of The Random Variable With The Following Probability Distribution This calculator finds mean, standard deviation and variance of a distribution. First, calculate the mean of the random variables. Variance (σ 2) = 0.9475. Standard deviation (σ) = 0.9734. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: We can use the following process to find the probability that a. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From socratic.org
The standard deviation of a normal random variable X is 20. Given that P(X Find The Standard Deviation Of The Random Variable With The Following Probability Distribution There are four steps to finding the standard deviation of random variables. The calculator will generate a step by step explanation along with. Standard deviation (σ) = 0.9734. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. This calculator finds mean, standard deviation. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.chegg.com
Solved Assume the random variable X is normally distributed Find The Standard Deviation Of The Random Variable With The Following Probability Distribution The calculator will generate a step by step explanation along with. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. First, calculate the mean. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From present5.com
CHAPTER 5 DISCRETE PROBABILITY DISTRIBUTIONS 1 2 Find The Standard Deviation Of The Random Variable With The Following Probability Distribution This calculator finds mean, standard deviation and variance of a distribution. The calculator will generate a step by step explanation along with. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: To find the variance σ 2 σ 2 of a. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.chegg.com
Solved A random variable is normally distributed with a mean Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Standard deviation (σ) = 0.9734. Variance (σ 2) = 0.9475. The calculator will generate a step by step explanation along with. This calculator finds mean, standard deviation and variance of a distribution. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation:. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.coursehero.com
[Solved] A random variable X follows normal distribution with mean = 5 Find The Standard Deviation Of The Random Variable With The Following Probability Distribution To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. This calculator finds mean, standard deviation and variance of a distribution. Variance (σ 2) = 0.9475. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From en.ppt-online.org
Probability Random Variables Preparatory Notes online presentation Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Variance (σ 2) = 0.9475. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. The. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.thoughtco.com
How to Calculate a Sample Standard Deviation Find The Standard Deviation Of The Random Variable With The Following Probability Distribution We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. Provide the outcomes of the random. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From teachoo.com
Example 9 Find variance and standard deviation Class 11 Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Variance (σ 2) = 0.9475. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: First, calculate the mean of the random variables. This calculator finds mean, standard deviation and variance of a distribution. Provide the outcomes of the random variable \((x)\),. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.slideshare.net
Variance and standard deviation of a discrete random variable Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: This calculator finds mean, standard deviation and variance of a distribution. First, calculate the mean of the random variables. The calculator will generate a step by step explanation along with. Standard deviation (σ) = 0.9734. There are four steps to finding. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.teachoo.com
Question 9 Random variable X has probability distribution P(X) = { k Find The Standard Deviation Of The Random Variable With The Following Probability Distribution This calculator finds mean, standard deviation and variance of a distribution. First, calculate the mean of the random variables. The calculator will generate a step by step explanation along with. Standard deviation (σ) = 0.9734. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.numerade.com
SOLVEDRandom variable X has normal distribution with mean and standard Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Standard deviation (σ) = 0.9734. Variance (σ 2) = 0.9475. There are four steps to finding the standard deviation of random variables. First, calculate the mean of the random variables. The calculator will generate a step by step explanation along with. This calculator finds mean, standard deviation and variance of a distribution. We can use the following process to find. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.youtube.com
Discrete random variables probability tables part 1 (Ex 82) YouTube Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Variance (σ 2) = 0.9475. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: First, calculate the mean of the random variables. This calculator finds mean, standard deviation and variance of a distribution. Standard deviation (σ) = 0.9734. The calculator will. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.chegg.com
Solved Assume the random variable X is normally distributed Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Variance (σ 2) = 0.9475. Standard deviation (σ) = 0.9734. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. The calculator will generate a step by step explanation along with. Provide the outcomes of the random variable \((x)\), as well as the associated. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.numerade.com
The table below represents the probability density function for the Find The Standard Deviation Of The Random Variable With The Following Probability Distribution There are four steps to finding the standard deviation of random variables. This calculator finds mean, standard deviation and variance of a distribution. Variance (σ 2) = 0.9475. The calculator will generate a step by step explanation along with. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From calcworkshop.com
Standard Deviation Variance Expected Value (2020) Find The Standard Deviation Of The Random Variable With The Following Probability Distribution First, calculate the mean of the random variables. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: The calculator will generate a step by step explanation along with. Variance (σ 2) = 0.9475. Standard deviation (σ) = 0.9734. We can use the following process to find the probability that a. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.youtube.com
Lesson 8.1 The Mean, Variance and Standard Deviation of a Discrete Find The Standard Deviation Of The Random Variable With The Following Probability Distribution This calculator finds mean, standard deviation and variance of a distribution. There are four steps to finding the standard deviation of random variables. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. The calculator will generate a step by step explanation along with.. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.teachoo.com
Example 12 Calculate mean, variance, standard deviation Find The Standard Deviation Of The Random Variable With The Following Probability Distribution There are four steps to finding the standard deviation of random variables. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. We can use the following process to find the probability that a normally distributed random variable x takes on a certain value,. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From mavink.com
Standard Normal Random Variable Table Find The Standard Deviation Of The Random Variable With The Following Probability Distribution We can use the following process to find the probability that a normally distributed random variable x takes on a certain value, given a mean and standard deviation: Variance (σ 2) = 0.9475. This calculator finds mean, standard deviation and variance of a distribution. Standard deviation (σ) = 0.9734. Provide the outcomes of the random variable \((x)\), as well as. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.chegg.com
Solved Compute the mean and standard deviation of the random Find The Standard Deviation Of The Random Variable With The Following Probability Distribution To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. This calculator finds mean, standard deviation and variance of a distribution. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: First, calculate the mean. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From youtube.com
Mean and Expected Value of Discrete Random Variables YouTube Find The Standard Deviation Of The Random Variable With The Following Probability Distribution To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. There are four steps to finding the standard deviation of random variables. First, calculate the mean of the random variables. Standard deviation (σ) = 0.9734. We can use the following process to find the. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.youtube.com
Variance and standard deviation of a discrete random variable AP Find The Standard Deviation Of The Random Variable With The Following Probability Distribution This calculator finds mean, standard deviation and variance of a distribution. Variance (σ 2) = 0.9475. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. We can use the following process to find the probability that a normally distributed random variable x takes. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From www.bartleby.com
Answered Assume the random variable X is… bartleby Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Variance (σ 2) = 0.9475. The calculator will generate a step by step explanation along with. This calculator finds mean, standard deviation and variance of a distribution. To find the variance σ 2 σ 2 of a discrete probability distribution, find each deviation from its expected value, square it, multiply it by its. First, calculate the mean of the random. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.
From melvinthavey.blogspot.com
Finding Probability of Random Continuous Variable Melvin Thavey Find The Standard Deviation Of The Random Variable With The Following Probability Distribution Variance (σ 2) = 0.9475. First, calculate the mean of the random variables. Provide the outcomes of the random variable \((x)\), as well as the associated probabilities \((p(x))\), in the form below: Standard deviation (σ) = 0.9734. The calculator will generate a step by step explanation along with. We can use the following process to find the probability that a. Find The Standard Deviation Of The Random Variable With The Following Probability Distribution.