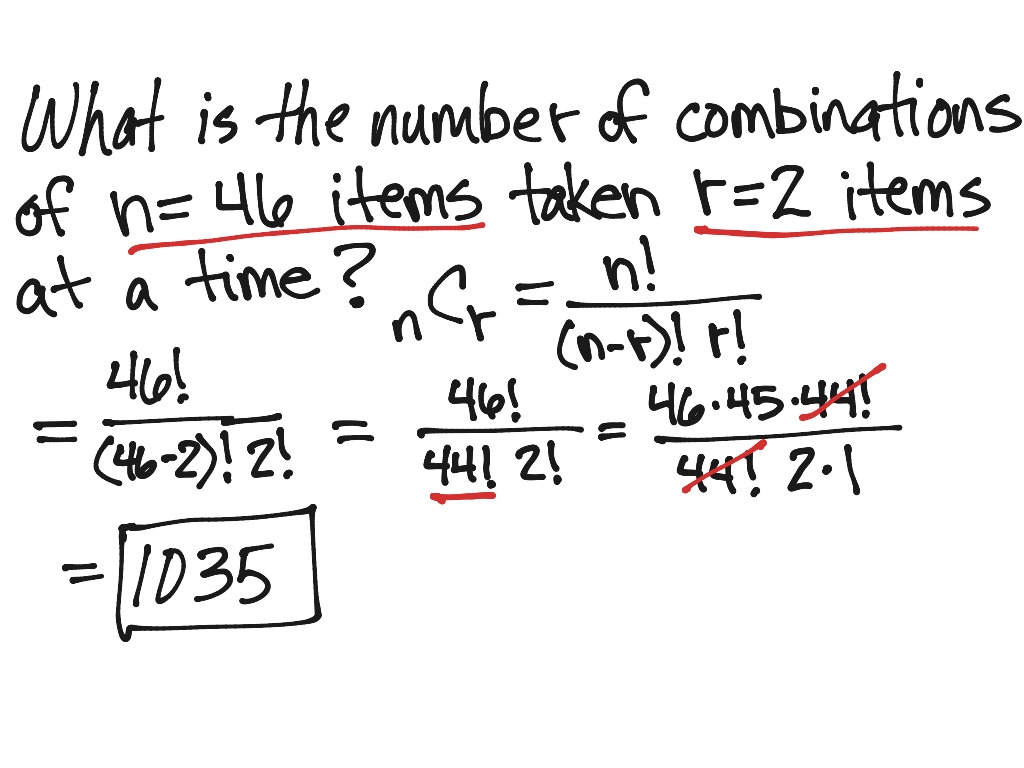Combinations Geometry . The number of combinations of n different things taken r at a time,. Combination formula and its derivation. Difference between permutation and combination. Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. After reading this article, you should understand: A combination is a way of choosing elements from a set in which order does not matter. In situations in which the order of a list of objects doesn’t matter, the lists are no longer. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where the order in which the objects are.
from criticalthinking.cloud
After reading this article, you should understand: The number of combinations of n different things taken r at a time,. Combination formula and its derivation. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. Difference between permutation and combination. A combination is a way of choosing elements from a set in which order does not matter. Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. In situations in which the order of a list of objects doesn’t matter, the lists are no longer. A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where the order in which the objects are. In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(.
solving combination problems
Combinations Geometry Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. Combination formula and its derivation. The number of combinations of n different things taken r at a time,. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. In situations in which the order of a list of objects doesn’t matter, the lists are no longer. A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where the order in which the objects are. A combination is a way of choosing elements from a set in which order does not matter. Difference between permutation and combination. After reading this article, you should understand:
From www.pinterest.com
Combination Calculator Studying math, Math methods, Math formulas Combinations Geometry A combination is a way of choosing elements from a set in which order does not matter. The number of combinations of n different things taken r at a time,. A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where the order in which the objects are. After reading this article, you. Combinations Geometry.
From www.youtube.com
KutaSoftware Geometry Permutations Vs Combinations YouTube Combinations Geometry In situations in which the order of a list of objects doesn’t matter, the lists are no longer. The number of combinations of n different things taken r at a time,. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. In. Combinations Geometry.
From www.showme.com
Combinations Math ShowMe Combinations Geometry In situations in which the order of a list of objects doesn’t matter, the lists are no longer. Combination formula and its derivation. After reading this article, you should understand: The number of combinations of n different things taken r at a time,. A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of. Combinations Geometry.
From www.askmattrab.com
Permutations and Combinations Class Twelve Maths Combinations Geometry In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. Difference between permutation and combination. Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. After reading this article, you should understand: A combination, sometimes called a binomial coefficient, is. Combinations Geometry.
From www.showme.com
Combinations versus Permutations Math ShowMe Combinations Geometry A combination is a way of choosing elements from a set in which order does not matter. Difference between permutation and combination. Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. The number of combinations of n different things taken r at a time,. In situations in which the order of. Combinations Geometry.
From eduinput.com
10 Examples of Combinations in Math Combinations Geometry In situations in which the order of a list of objects doesn’t matter, the lists are no longer. Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated. Combinations Geometry.
From www.cuemath.com
Combinations Definition, Formula, Examples, FAQs Combinations Geometry In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. After reading this article, you should understand: In situations in which the order of a list of objects doesn’t matter, the lists are no longer. Combinations refer to the possible arrangements of a set of given objects when. Combinations Geometry.
From www.pinterest.com
An Overview of Combinations and Permutations Math formulas, Math time Combinations Geometry The number of combinations of n different things taken r at a time,. After reading this article, you should understand: Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. In general, the number of ways to pick \( k \) unordered. Combinations Geometry.
From www.cuemath.com
Permutation and Combination Definition, Formulas, Derivation, Examples Combinations Geometry After reading this article, you should understand: In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. A combination is a way of choosing elements from a set in which order does not matter. In situations in which the order of a list of objects doesn’t matter, the. Combinations Geometry.
From www.mindomo.com
Permutation and Combination Mind Map Combinations Geometry After reading this article, you should understand: A combination is a way of choosing elements from a set in which order does not matter. Combination formula and its derivation. Difference between permutation and combination. The number of combinations of n different things taken r at a time,. In situations in which the order of a list of objects doesn’t matter,. Combinations Geometry.
From www.youtube.com
Geometry 132 Probability with Permutations and Combinations Part 1 Combinations Geometry Difference between permutation and combination. A combination is a way of choosing elements from a set in which order does not matter. A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where the order in which the objects are. Combinations refer to the possible arrangements of a set of given objects when. Combinations Geometry.
From www.youtube.com
Combination Math 10 Quarter 3 YouTube Combinations Geometry The number of combinations of n different things taken r at a time,. Difference between permutation and combination. After reading this article, you should understand: Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. In general, the number of ways to. Combinations Geometry.
From scienceres-edcp-educ.sites.olt.ubc.ca
Statistics and Probability MSTLTT Combinations Geometry Difference between permutation and combination. A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where the order in which the objects are. The number of combinations of n different things taken r at a time,. Combinations are selections made by taking some or all of a number of objects, irrespective of their. Combinations Geometry.
From www.youtube.com
The Combination Formula and Why it Works Combinatorics, Combinations Combinations Geometry A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where the order in which the objects are. The number of combinations of n different things taken r at a time,. In situations in which the order of a list of objects doesn’t matter, the lists are no longer. In general, the number. Combinations Geometry.
From criticalthinking.cloud
solving combination problems Combinations Geometry A combination is a way of choosing elements from a set in which order does not matter. In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. Combination formula and its derivation. After reading this article, you should understand: Combinations refer to the possible arrangements of a set. Combinations Geometry.
From printablefullmongo.z13.web.core.windows.net
Combinations And Permutations Math Combinations Geometry The number of combinations of n different things taken r at a time,. In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. Difference between permutation and combination. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the. Combinations Geometry.
From www.slideserve.com
PPT Combinations & Permutations PowerPoint Presentation, free Combinations Geometry In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. The number of combinations of n different things taken r at a time,. Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. Combination formula and its derivation. Difference between. Combinations Geometry.
From www.youtube.com
Discrete Math 2 Tutorial 4 Combinations YouTube Combinations Geometry Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. The number of combinations of n different things taken r at a time,. Combination formula and its derivation. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated. Combinations Geometry.
From www.slideserve.com
PPT Lesson 58 Combinations PowerPoint Presentation, free download Combinations Geometry Difference between permutation and combination. The number of combinations of n different things taken r at a time,. In situations in which the order of a list of objects doesn’t matter, the lists are no longer. Combination formula and its derivation. After reading this article, you should understand: In general, the number of ways to pick \( k \) unordered. Combinations Geometry.
From www.youtube.com
Introduction to Permutations and Combinations YouTube Combinations Geometry Combination formula and its derivation. A combination is a way of choosing elements from a set in which order does not matter. The number of combinations of n different things taken r at a time,. After reading this article, you should understand: A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where. Combinations Geometry.
From www.cuemath.com
Geometry Formulas All Geometry Formulas 2D and 3D Geometry Formulas Combinations Geometry In situations in which the order of a list of objects doesn’t matter, the lists are no longer. A combination is a way of choosing elements from a set in which order does not matter. Difference between permutation and combination. Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. After reading. Combinations Geometry.
From www.slideserve.com
PPT Permutations and Combinations PowerPoint Presentation, free Combinations Geometry A combination is a way of choosing elements from a set in which order does not matter. Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. The number of combinations of n different things taken r at a time,. Difference between permutation and combination. A combination, sometimes called a binomial coefficient,. Combinations Geometry.
From learningzonewalsh.z21.web.core.windows.net
Combinations Of 10 Math Combinations Geometry In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. The number of combinations of n different things taken r at a time,. After reading this article, you should understand: Difference between permutation and combination. A combination is a way of choosing elements from a set in which. Combinations Geometry.
From www.math-salamanders.com
List of Geometric Shapes Combinations Geometry Combination formula and its derivation. The number of combinations of n different things taken r at a time,. A combination is a way of choosing elements from a set in which order does not matter. In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. In situations in. Combinations Geometry.
From www.pinterest.com.au
Pin on school Combinations Geometry Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. The number of combinations of n different things taken r. Combinations Geometry.
From www.studypug.com
Introduction to combinations StudyPug Combinations Geometry After reading this article, you should understand: In situations in which the order of a list of objects doesn’t matter, the lists are no longer. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. The number of combinations of n different. Combinations Geometry.
From calcworkshop.com
Combinations (Illustrated w/ 11+ Worked Examples!) Combinations Geometry Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. Difference between permutation and combination. In situations in which the order of a list. Combinations Geometry.
From www.youtube.com
Combinations (Simplifying Math) YouTube Combinations Geometry A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where the order in which the objects are. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. Combination formula and its derivation. The number. Combinations Geometry.
From www.youtube.com
Solving Systems Using Linear Combination (Simplifying Math) YouTube Combinations Geometry A combination is a way of choosing elements from a set in which order does not matter. The number of combinations of n different things taken r at a time,. Combination formula and its derivation. A combination, sometimes called a binomial coefficient, is a way of choosing objects from a set of where the order in which the objects are.. Combinations Geometry.
From www.youtube.com
Solving Systems of Linear Equations Linear Combination Method YouTube Combinations Geometry In situations in which the order of a list of objects doesn’t matter, the lists are no longer. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. After reading this article, you should understand: Difference between permutation and combination. Combination formula. Combinations Geometry.
From e-gmat.com
Difference between Permutation and Combination explained with examples Combinations Geometry In situations in which the order of a list of objects doesn’t matter, the lists are no longer. A combination is a way of choosing elements from a set in which order does not matter. Combination formula and its derivation. After reading this article, you should understand: Combinations are selections made by taking some or all of a number of. Combinations Geometry.
From calcworkshop.com
Combinations (Illustrated w/ 11+ Worked Examples!) Combinations Geometry A combination is a way of choosing elements from a set in which order does not matter. Combination formula and its derivation. The number of combinations of n different things taken r at a time,. In situations in which the order of a list of objects doesn’t matter, the lists are no longer. Combinations refer to the possible arrangements of. Combinations Geometry.
From printablelibfigures.z19.web.core.windows.net
How To Do Combinations Math Combinations Geometry Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. After reading this article, you should understand: Combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. Combination formula and its derivation. Difference between. Combinations Geometry.
From www.slideserve.com
PPT Permutations and Combinations PowerPoint Presentation, free Combinations Geometry After reading this article, you should understand: In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. The number of combinations of n different things taken r at a time,. A combination is a way of choosing elements from a set in which order does not matter. A. Combinations Geometry.
From www.youtube.com
Maths Combination Part 1 ( Definition , Concept and Notation) Class X1 Combinations Geometry In general, the number of ways to pick \( k \) unordered elements from an \( n \) element set is \(. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. In situations in which the order of a list of. Combinations Geometry.