Extreme Points Definition . An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k. Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. Extreme points have applications beyond geometry; Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0, 1], then y =. They are important in economics for finding equilibria in various models. In two and three dimensions, the corners of a polyhedron are the extreme points. However, it would be a mistake to think that extreme points. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point.
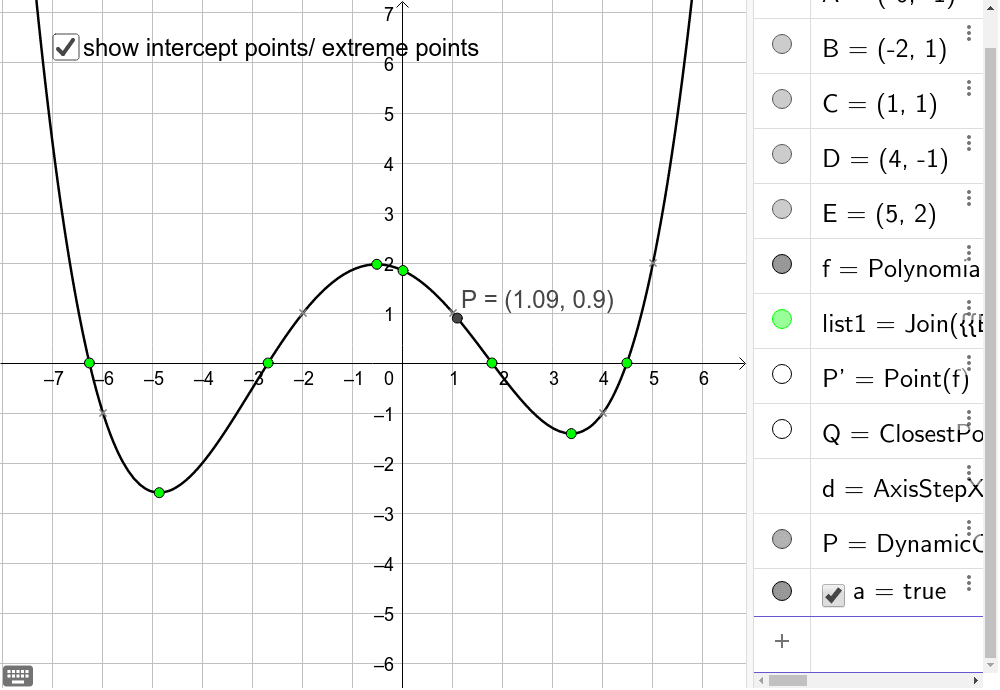
from www.geogebra.org
They are important in economics for finding equilibria in various models. Extreme points have applications beyond geometry; Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0, 1], then y =. An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. However, it would be a mistake to think that extreme points. Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. In two and three dimensions, the corners of a polyhedron are the extreme points.
Snapping to Intercept Points & Extreme Points GeoGebra
Extreme Points Definition Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0, 1], then y =. However, it would be a mistake to think that extreme points. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. In two and three dimensions, the corners of a polyhedron are the extreme points. Extreme points have applications beyond geometry; Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. They are important in economics for finding equilibria in various models. An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k.
From www.slideserve.com
PPT ISM 206 Lecture 3 PowerPoint Presentation, free download ID465472 Extreme Points Definition Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. In two and three dimensions, the corners of a polyhedron are the extreme points. Extreme points have applications beyond geometry; However, it would be a mistake to think that extreme points. Extreme points are the vertices of a feasible region. Extreme Points Definition.
From www.storyofmathematics.com
Relative Extrema Definition, Properties, and Examples Extreme Points Definition However, it would be a mistake to think that extreme points. They are important in economics for finding equilibria in various models. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0, 1], then y =. Extreme points. Extreme Points Definition.
From www.slideserve.com
PPT Chapter 2 Introduction to Linear Programming PowerPoint Extreme Points Definition However, it would be a mistake to think that extreme points. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z. Extreme Points Definition.
From www.youtube.com
EN how to find extreme points YouTube Extreme Points Definition Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. They are important in economics for finding equilibria in various models. Extreme points have applications beyond geometry; Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. In two and. Extreme Points Definition.
From www.youtube.com
Investigating The Extreme Points Of Countries & Continents (Part Two Extreme Points Definition Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. Extreme points have applications beyond geometry; In two and three dimensions, the corners of a polyhedron are the extreme points. Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an.. Extreme Points Definition.
From www.slideserve.com
PPT Introduction to Linear Programming PowerPoint Presentation, free Extreme Points Definition However, it would be a mistake to think that extreme points. Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. In two and three dimensions, the corners of a. Extreme Points Definition.
From www.slideserve.com
PPT 1.4 The Extreme Point Theorem Geometry of a linear programming Extreme Points Definition However, it would be a mistake to think that extreme points. In two and three dimensions, the corners of a polyhedron are the extreme points. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0, 1], then y. Extreme Points Definition.
From www.youtube.com
Extreme values and critical points Definition of local extrema YouTube Extreme Points Definition Extreme points have applications beyond geometry; They are important in economics for finding equilibria in various models. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. Definition an. Extreme Points Definition.
From www.slideserve.com
PPT Applications of Derivatives PowerPoint Presentation, free Extreme Points Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0, 1], then y =. They are important. Extreme Points Definition.
From www.slideserve.com
PPT Chapter 2 An Introduction to Linear Programming PowerPoint Extreme Points Definition Extreme points have applications beyond geometry; However, it would be a mistake to think that extreme points. An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum. Extreme Points Definition.
From www.slideserve.com
PPT Part 3. Linear Programming PowerPoint Presentation, free download Extreme Points Definition Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. However, it would be a mistake to think that extreme points. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. Extreme points have applications beyond geometry; They are. Extreme Points Definition.
From www.slideserve.com
PPT Applications of Derivatives PowerPoint Presentation, free Extreme Points Definition Extreme points have applications beyond geometry; Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0, 1], then y =. In two and three dimensions, the corners of a polyhedron are the extreme points. An extreme point of. Extreme Points Definition.
From slideplayer.com
Chap 2. The Geometry of LP In the text, polyhedron is defined as ppt Extreme Points Definition Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. They are important in economics for finding equilibria in various models. Definition an extreme point of a convex set, a,. Extreme Points Definition.
From www.slideserve.com
PPT Linear Programming PowerPoint Presentation, free download ID Extreme Points Definition An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k. They are important in economics for finding equilibria in various models. Extreme points have applications beyond geometry; Extreme points are the vertices or corner points of a convex set, representing the most. Extreme Points Definition.
From www.slideserve.com
PPT Optimization Methods PowerPoint Presentation, free download ID Extreme Points Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. However, it would be a mistake to think that extreme points. An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k.. Extreme Points Definition.
From www.slideserve.com
PPT Chapter 2 Introduction to Linear Programming PowerPoint Extreme Points Definition In two and three dimensions, the corners of a polyhedron are the extreme points. Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. They are important in economics for. Extreme Points Definition.
From calcworkshop.com
Absolute Extrema (How To Find 'Em w/ 17 Examples!) Extreme Points Definition In two and three dimensions, the corners of a polyhedron are the extreme points. Extreme points have applications beyond geometry; A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. They are important in economics for finding equilibria in various models. An extreme point of a subset k of. Extreme Points Definition.
From www.slideserve.com
PPT Applications of Derivatives PowerPoint Presentation, free Extreme Points Definition In two and three dimensions, the corners of a polyhedron are the extreme points. However, it would be a mistake to think that extreme points. Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. Definition an extreme point of a convex set, a, is a point x a, with. Extreme Points Definition.
From www.researchgate.net
Curve fitting of extreme points Download Scientific Diagram Extreme Points Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. They are important in economics for finding equilibria in various models. However, it would be a mistake to think that extreme points. An extreme point of a subset k of a vector space x is an extreme set s. Extreme Points Definition.
From www.researchgate.net
Example of extreme points. Download Scientific Diagram Extreme Points Definition Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0, 1], then y =. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. In two and. Extreme Points Definition.
From www.slideserve.com
PPT Applications of Derivatives PowerPoint Presentation, free Extreme Points Definition Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is. Extreme Points Definition.
From www.slideserve.com
PPT Applications of Derivatives PowerPoint Presentation, free Extreme Points Definition Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. However, it would be a mistake to think that extreme points. Extreme points have applications beyond geometry; A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. They are. Extreme Points Definition.
From www.geogebra.org
Snapping to Intercept Points & Extreme Points GeoGebra Extreme Points Definition Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. They are important in economics for finding equilibria in various models. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. In two and three dimensions, the corners of. Extreme Points Definition.
From www.researchgate.net
Position of extreme points and inflection points on toolpath Download Extreme Points Definition In two and three dimensions, the corners of a polyhedron are the extreme points. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z. Extreme Points Definition.
From www.slideserve.com
PPT PARETO LINEAR PROGRAMMING PowerPoint Presentation, free download Extreme Points Definition A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. In two and three dimensions, the corners of a polyhedron are the extreme points. Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. However, it would be a. Extreme Points Definition.
From www.slideserve.com
PPT Applications of Derivatives PowerPoint Presentation, free Extreme Points Definition However, it would be a mistake to think that extreme points. Extreme points have applications beyond geometry; An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k. Definition an extreme point of a convex set, a, is a point x a, with. Extreme Points Definition.
From www.going2paris.net
Extremes Points In The United States Extreme Points Definition They are important in economics for finding equilibria in various models. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0, 1], then y =. Extreme points are the vertices of a feasible region in optimization problems, where. Extreme Points Definition.
From www.slideserve.com
PPT 1.4 The Extreme Point Theorem Geometry of a linear programming Extreme Points Definition Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. Extreme points have applications beyond geometry; A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. Extreme points are the vertices of a feasible region in optimization problems, where. Extreme Points Definition.
From www.researchgate.net
the principle of extreme points. Download Scientific Diagram Extreme Points Definition However, it would be a mistake to think that extreme points. Extreme points have applications beyond geometry; In two and three dimensions, the corners of a polyhedron are the extreme points. They are important in economics for finding equilibria in various models. Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values. Extreme Points Definition.
From www.youtube.com
Find and classify extreme points of f YouTube Extreme Points Definition Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. A saddle point is a point \((x_0,y_0)\) where \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\), but \(f(x_0,y_0)\) is neither a maximum nor a minimum at that point. An extreme point of a subset k of a vector space x is an extreme set s of k. Extreme Points Definition.
From www.slideserve.com
PPT Applications of Derivatives PowerPoint Presentation, free Extreme Points Definition They are important in economics for finding equilibria in various models. In two and three dimensions, the corners of a polyhedron are the extreme points. An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k. Extreme points are the vertices or corner. Extreme Points Definition.
From derivative-calculators.com
Extreme Points Calculator Find Extreme and Saddle Points Extreme Points Definition Extreme points have applications beyond geometry; Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. However, it would be a mistake to think that extreme points. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy +. Extreme Points Definition.
From www.vrogue.co
Points And Lines Definition Examples Cuemath vrogue.co Extreme Points Definition An extreme point of a subset k of a vector space x is an extreme set s of k which consists of a single point x in k. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a and θ [0,. Extreme Points Definition.
From www.researchgate.net
Example for the different extreme points. Download Scientific Diagram Extreme Points Definition Extreme points are the vertices or corner points of a convex set, representing the most 'outward' positions within that set. However, it would be a mistake to think that extreme points. Definition an extreme point of a convex set, a, is a point x a, with the property that if x = θy + (1 θ)z with y, z a. Extreme Points Definition.
From slideplayer.com
EMGT 6412/MATH 6665 Mathematical Programming Spring ppt download Extreme Points Definition In two and three dimensions, the corners of a polyhedron are the extreme points. Extreme points are the vertices of a feasible region in optimization problems, where the maximum or minimum values of an. However, it would be a mistake to think that extreme points. Definition an extreme point of a convex set, a, is a point x a, with. Extreme Points Definition.