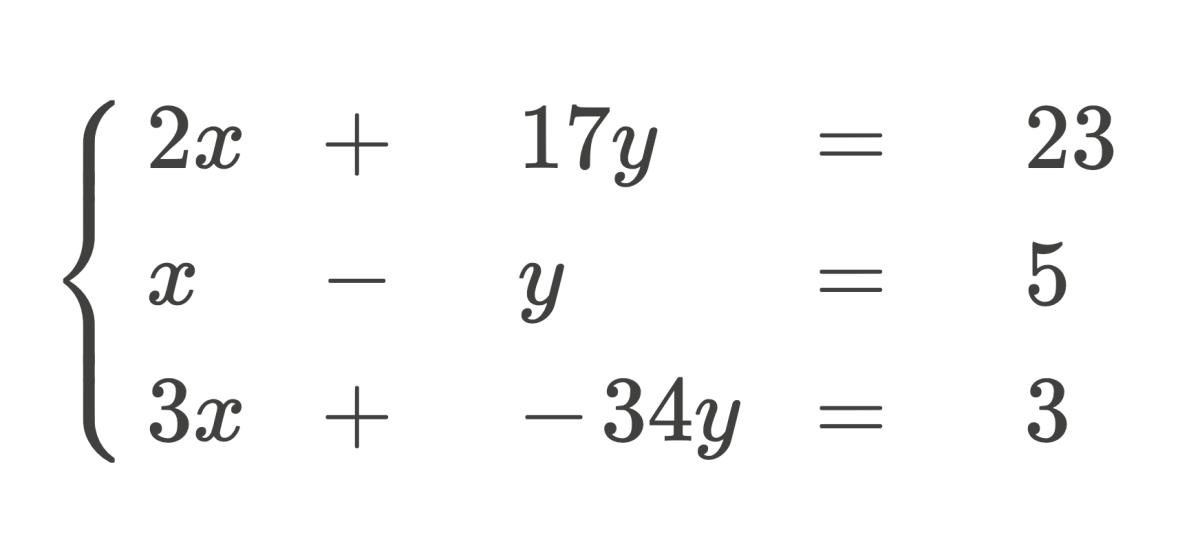Linear Algebra 1.3 . Learn to express the solution set of a system of linear equations in parametric form. We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Understand the three possibilities for the number of solutions of a system of linear equations. Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous.
from owlcation.com
Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. Learn to express the solution set of a system of linear equations in parametric form. Understand the three possibilities for the number of solutions of a system of linear equations. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2. We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections.
An Introduction to Linear Algebra Owlcation
Linear Algebra 1.3 Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Understand the three possibilities for the number of solutions of a system of linear equations. Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). Learn to express the solution set of a system of linear equations in parametric form. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2.
From videos.mathtutordvd.com
Linear Algebra Vol 1 Math Tutor Public Gallery Linear Algebra 1.3 The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Learn to express the solution set of a system of linear equations in parametric form. Our interest in linear. Linear Algebra 1.3.
From www.studocu.com
Tutorial 1 mtl101 MTL101 Tutorial 1 Linear Algebra (1) Suppose Linear Algebra 1.3 We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. Learn to express the solution set of a. Linear Algebra 1.3.
From www.scribd.com
Linear Algebra1 PDF Linear Algebra 1.3 The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. What is the area of the parallelogram with vertices \((0,0,0)\),. Linear Algebra 1.3.
From www.studocu.com
Lineare Algebra I S13 Meike Akveld Serie 13 Determinanten (Teil 2 Linear Algebra 1.3 Learn to express the solution set of a system of linear equations in parametric form. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. Understand the three possibilities. Linear Algebra 1.3.
From www.studocu.com
Review Linear Algebra 1 Linear algebra In this section we will Linear Algebra 1.3 What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. Learn to express the solution set of a system of linear equations in parametric form. Lecture notes for linear. Linear Algebra 1.3.
From www.studypool.com
SOLUTION Review linear algebra 1 Studypool Linear Algebra 1.3 Learn to express the solution set of a system of linear equations in parametric form. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Understand the three possibilities for the number of solutions. Linear Algebra 1.3.
From www.slideserve.com
PPT Linear Algebra PowerPoint Presentation ID150375 Linear Algebra 1.3 Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Learn to express the solution set of a system of linear equations. Linear Algebra 1.3.
From www.studocu.com
Math136 w23 wpp3 1 Math 136 MATH136 Linear Algebra 1 Week 3 Linear Algebra 1.3 Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. Learn to express the solution set of a system of linear equations in parametric form.. Linear Algebra 1.3.
From studylibde.com
¨Ubungen zur Linearen Algebra I Linear Algebra 1.3 Learn to express the solution set of a system of linear equations in parametric form. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2. We will. Linear Algebra 1.3.
From www.studypool.com
SOLUTION Review linear algebra 1 Studypool Linear Algebra 1.3 Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) ,. Linear Algebra 1.3.
From www.studocu.com
Problems MATH2501 Linear Algebra, S1 2015 Problems Linear Algebra 1.3 Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2. Understand the three possibilities for the number of solutions of a system of linear equations. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i. Linear Algebra 1.3.
From www.studocu.com
Linear algebra1 5 good Matrix Algebra Example 9. Compute A 3 if A Linear Algebra 1.3 What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). Lecture notes for. Linear Algebra 1.3.
From towardsdatascience.com
Linear Algebra 1 Linear Equations and Systems by tenzin migmar (t9nz Linear Algebra 1.3 Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and. Linear Algebra 1.3.
From studylibde.com
Lineare Algebra 1 Linear Algebra 1.3 Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). Learn to express the solution set of a. Linear Algebra 1.3.
From www.studocu.com
1 Techniques Of Classical And Linear Algebra detailed notes Chapter Linear Algebra 1.3 What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Learn to express the solution set of a system of linear equations in parametric form. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Understand the three possibilities. Linear Algebra 1.3.
From www.studocu.com
Linear algebra1 0 good Linear Independence Example 6. Consider the Linear Algebra 1.3 Understand the three possibilities for the number of solutions of a system of linear equations. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections.. Linear Algebra 1.3.
From elf-c.he.u-tokyo.ac.jp
1.3. Quiz Linear Algebra Lecture 1 The Geometry of Linear Equations Linear Algebra 1.3 Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Understand the three possibilities for the number of solutions of. Linear Algebra 1.3.
From www.studypool.com
SOLUTION Mh1200 linear algebra 1 midterms 1415 solution Studypool Linear Algebra 1.3 We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). Learn to express the solution set of a system of linear equations in parametric form. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. Our interest in linear combinations comes from the fact. Linear Algebra 1.3.
From www.studocu.com
Linear algebra Linear Algebra David Cherney, Tom Denton, Rohit Thomas Linear Algebra 1.3 The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). Our interest in linear combinations comes from the fact that they provide one of the best ways to describe. Linear Algebra 1.3.
From www.youtube.com
Linear Algebra 3 Finding Number of Solutions YouTube Linear Algebra 1.3 The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. Understand the three possibilities for the number of solutions of. Linear Algebra 1.3.
From www.studocu.com
CW7sol2020 All lectures and course sheets on linear algebra 1 Linear Algebra 1.3 Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. Learn to express the solution set of a system of linear equations in parametric form. Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and. Linear Algebra 1.3.
From www.studocu.com
Lineare Algebra 1 Blatt 12 Loesung, Aufgaben 2 und 3 WS 18/19 Linear Algebra 1.3 The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Learn to express the solution set of a system of linear equations in parametric form. Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the. Linear Algebra 1.3.
From studylib.net
Linear Algebra Linear Algebra 1.3 Learn to express the solution set of a system of linear equations in parametric form. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. We will denote the. Linear Algebra 1.3.
From www.studocu.com
Intro TO Linear Algebra 1.2 System of Equations 1 Systems of Linear Algebra 1.3 What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Understand the three possibilities for the number of solutions of a system of linear equations. Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2. Learn to express the solution set. Linear Algebra 1.3.
From www.studypool.com
SOLUTION Mh1200 linear algebra 1 midterms 1415 solution Studypool Linear Algebra 1.3 Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2. Understand the three possibilities for the number of solutions of a system of linear equations. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? The technique used to multiply two. Linear Algebra 1.3.
From www.digitaled.com
Linear Algebra I DigitalEd Linear Algebra 1.3 Understand the three possibilities for the number of solutions of a system of linear equations. Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. Learn to. Linear Algebra 1.3.
From www.thinkswap.com
MA1101R Linear Algebra I Summary MA2001 Linear Algebra 1 NUS Linear Algebra 1.3 Learn to express the solution set of a system of linear equations in parametric form. Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Lecture notes for linear. Linear Algebra 1.3.
From www.studocu.com
11 Übungsblatt Lineare Algebra ——————————————————————— L i n e a r Linear Algebra 1.3 Understand the three possibilities for the number of solutions of a system of linear equations. We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? The technique used to multiply two matrices together requires us to move across. Linear Algebra 1.3.
From www.studocu.com
Section 2.3_Int to Linear Algebra 1640251 Studocu Linear Algebra 1.3 What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Learn to express. Linear Algebra 1.3.
From www.studocu.com
1 Linear Algebra 1 All Branches Hinglish Subject Engineering Linear Algebra 1.3 Understand the three possibilities for the number of solutions of a system of linear equations. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections.. Linear Algebra 1.3.
From dokumen.tips
(PDF) Chapter 1 Basic Linear Algebra 1_1314 Mode Linear Algebra 1.3 What is the area of the parallelogram with vertices \((0,0,0)\), \((1,2,1)\), \((3,1,1)\) and \((4, 3, 2)\)? Understand the three possibilities for the number of solutions of a system of linear equations. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Lecture notes for linear. Linear Algebra 1.3.
From owlcation.com
An Introduction to Linear Algebra Owlcation Linear Algebra 1.3 The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Understand the three possibilities for the number of solutions of a system of linear equations. Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections.. Linear Algebra 1.3.
From www.thenile.com.au
Linear Algebra I Basic Concepts by Kazuo Murota, Hardcover Linear Algebra 1.3 Lecture notes for linear algebra (2021) table of contents preface to the notes textbooks, websites, and video lectures sample sections. Learn to express the solution set of a system of linear equations in parametric form. Suppose every u 2 u can be uniquely written as u = u1 + u2 for u1 2 u1 and u2 2 u2. Understand the. Linear Algebra 1.3.
From desklib.com
LINEAR ALGEBRA 1 Linear Algebra Name Institution Linear Algebra 1.3 Understand the three possibilities for the number of solutions of a system of linear equations. Learn to express the solution set of a system of linear equations in parametric form. The technique used to multiply two matrices together requires us to move across the horizontal rows of the first matrix (the i index) and down. Our interest in linear combinations. Linear Algebra 1.3.
From www.studocu.com
Hw3 Homework 3 for MATH 1250 Linear Algebra 1 MATH1250 Linear Linear Algebra 1.3 Our interest in linear combinations comes from the fact that they provide one of the best ways to describe the general solution of a homogeneous. We will denote the points \((1,2,1)\) , \((3,1,1)\) and \((4, 3, 2)\) as \(p\) , \(q\). The technique used to multiply two matrices together requires us to move across the horizontal rows of the first. Linear Algebra 1.3.