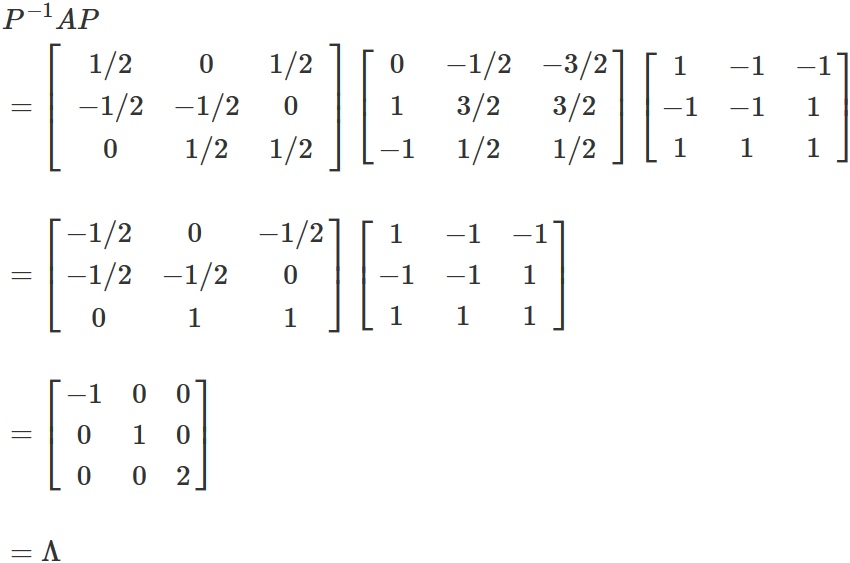Orthogonally Diagonalizable Matrix Example . An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. \(a\) is orthogonally diagonalizable. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. So any real symmetric matrix is orthogonally diagonalizable. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. example if e is any matrix (square or not), then e x e is square. E x e is also symmetric because ðe x eñ. We have seen examples of.
from semath.info
An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. So any real symmetric matrix is orthogonally diagonalizable. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. We have seen examples of. \(a\) is orthogonally diagonalizable. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. E x e is also symmetric because ðe x eñ.
How to diagonalize a 3x3 matrix Example SEMATH INFO
Orthogonally Diagonalizable Matrix Example example if e is any matrix (square or not), then e x e is square. \(a\) is orthogonally diagonalizable. So any real symmetric matrix is orthogonally diagonalizable. example if e is any matrix (square or not), then e x e is square. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. E x e is also symmetric because ðe x eñ. We have seen examples of. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable.
From rebeccamorford.blogspot.com
Symmetric Matrix Orthogonally Diagonalizable Rebecca Morford's Orthogonally Diagonalizable Matrix Example an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. We have seen examples of. example if e is any matrix (square or not), then e x. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonally Diagonalizable Matrix Example Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. example if e is any matrix (square or not), then e x e is square. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. So any real symmetric matrix is orthogonally diagonalizable. \(a\). Orthogonally Diagonalizable Matrix Example.
From www.youtube.com
Diagonalize 3x3 matrix YouTube Orthogonally Diagonalizable Matrix Example orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. \(a\) is orthogonally diagonalizable. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. We have seen examples. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize matrix A given below; that Orthogonally Diagonalizable Matrix Example an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. example if e is any matrix (square or not), then e x e is square. We have seen examples of. E x e is also symmetric because ðe x eñ. So any real symmetric matrix is orthogonally diagonalizable. \(a\) is orthogonally diagonalizable. . Orthogonally Diagonalizable Matrix Example.
From www.slideserve.com
PPT Diagonal Matrix PowerPoint Presentation, free download ID5424371 Orthogonally Diagonalizable Matrix Example \(a\) is orthogonally diagonalizable. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. We have seen examples of. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n. Orthogonally Diagonalizable Matrix Example.
From www.youtube.com
Orthogonally Diagonalize a Matrix YouTube Orthogonally Diagonalizable Matrix Example example if e is any matrix (square or not), then e x e is square. We have seen examples of. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonally Diagonalizable Matrix Example in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. An n×n n × n. Orthogonally Diagonalizable Matrix Example.
From calcworkshop.com
Diagonalization of Symmetric Matrices (Steps & Strategies) Orthogonally Diagonalizable Matrix Example E x e is also symmetric because ðe x eñ. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. example if e is any matrix (square or not), then e x e is square. an n nmatrix a is symmetric if and. Orthogonally Diagonalizable Matrix Example.
From www.bartleby.com
Answered Orthogonally diagonalize the matrix,… bartleby Orthogonally Diagonalizable Matrix Example orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. So any real symmetric matrix is orthogonally diagonalizable. example if e is any matrix (square or not), then e x e. Orthogonally Diagonalizable Matrix Example.
From www.coursehero.com
[Solved] Q1 Q2 Q3 THANK YOU!. Orthogonally diagonalize the matrix Orthogonally Diagonalizable Matrix Example An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. \(a\) is orthogonally diagonalizable. orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. in the following example, the orthogonal matrix \(u\) will be. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalizable the matrix, giving an Orthogonally Diagonalizable Matrix Example \(a\) is orthogonally diagonalizable. example if e is any matrix (square or not), then e x e is square. So any real symmetric matrix is orthogonally diagonalizable. E x e is also symmetric because ðe x eñ. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. An n×n n × n matrix. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrices in Exercises Orthogonally Diagonalizable Matrix Example Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. E x e is also symmetric because ðe x eñ. an n nmatrix a is symmetric if. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonally Diagonalizable Matrix Example example if e is any matrix (square or not), then e x e is square. \(a\) is orthogonally diagonalizable. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. an \(n\times n\) matrix \(a\) is. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved (1 point) Orthogonally diagonalize the matrix 1 02 Orthogonally Diagonalizable Matrix Example An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. So any real symmetric matrix is orthogonally diagonalizable. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. E x e is also symmetric because ðe x eñ. orthogonally. Orthogonally Diagonalizable Matrix Example.
From www.slideserve.com
PPT 5.1 Orthogonality PowerPoint Presentation, free download ID2094487 Orthogonally Diagonalizable Matrix Example \(a\) is orthogonally diagonalizable. So any real symmetric matrix is orthogonally diagonalizable. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1}. Orthogonally Diagonalizable Matrix Example.
From leonardnavdar.blogspot.com
Diagonalize matrix calculator LeonardNavdar Orthogonally Diagonalizable Matrix Example E x e is also symmetric because ðe x eñ. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. \(a\) is orthogonally diagonalizable. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. in the following example,. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonally Diagonalizable Matrix Example orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. We have seen examples of. example if e is any matrix (square or not), then e x e is square. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. an n. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrices in Exercises Orthogonally Diagonalizable Matrix Example an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. We have seen examples of. E x e is also symmetric because. Orthogonally Diagonalizable Matrix Example.
From www.youtube.com
Orthogonal Diagonalization YouTube Orthogonally Diagonalizable Matrix Example in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. So any real symmetric matrix is orthogonally diagonalizable. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. an \(n\times n\) matrix \(a\) is diagonalizable if and. Orthogonally Diagonalizable Matrix Example.
From eevibes.com
How to diagonalize a matrix? Example of diagonalization EEVibes Orthogonally Diagonalizable Matrix Example An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonally Diagonalizable Matrix Example We have seen examples of. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. \(a\) is orthogonally. Orthogonally Diagonalizable Matrix Example.
From www.youtube.com
Orthogonally Diagonalizable Matrices YouTube Orthogonally Diagonalizable Matrix Example E x e is also symmetric because ðe x eñ. orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. example if e is any matrix (square or not), then e x e is square. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if. Orthogonally Diagonalizable Matrix Example.
From www.youtube.com
Week 10 Symmetric matrices and orthogonal diagonalization YouTube Orthogonally Diagonalizable Matrix Example example if e is any matrix (square or not), then e x e is square. E x e is also symmetric because ðe x eñ. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. an \(n\times n\) matrix \(a\) is diagonalizable if. Orthogonally Diagonalizable Matrix Example.
From www.slideserve.com
PPT 8.2 Orthogonal Diagonalization PowerPoint Presentation, free Orthogonally Diagonalizable Matrix Example example if e is any matrix (square or not), then e x e is square. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. E x e is also symmetric because ðe x eñ. So any real symmetric matrix is orthogonally diagonalizable. . Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonally Diagonalizable Matrix Example in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. Recall (theorem 5.5.3) that an. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved 1. Diagonalize the following matrices or determine Orthogonally Diagonalizable Matrix Example in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. example if e is any matrix (square or not), then e x e is square. \(a\) is orthogonally diagonalizable. E x e is also symmetric because ðe x eñ. an n nmatrix a is symmetric if and only if it. Orthogonally Diagonalizable Matrix Example.
From rebeccamorford.blogspot.com
Symmetric Matrix Orthogonally Diagonalizable Rebecca Morford's Orthogonally Diagonalizable Matrix Example E x e is also symmetric because ðe x eñ. So any real symmetric matrix is orthogonally diagonalizable. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. \(a\) is orthogonally diagonalizable. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix. Orthogonally Diagonalizable Matrix Example.
From www.slideserve.com
PPT Diagonal Matrix PowerPoint Presentation, free download ID5424371 Orthogonally Diagonalizable Matrix Example an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p. Orthogonally Diagonalizable Matrix Example.
From www.youtube.com
Orthogonal Diagonalization Orthogonally Diagonalize a Square Matrix Orthogonally Diagonalizable Matrix Example an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. E x e is also symmetric because ðe x eñ. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. So any real symmetric matrix is orthogonally diagonalizable. example if e is any matrix (square. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonally Diagonalizable Matrix Example So any real symmetric matrix is orthogonally diagonalizable. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. example if e is any matrix (square or not), then e. Orthogonally Diagonalizable Matrix Example.
From www.youtube.com
Diagonalising a 2x2 matrix YouTube Orthogonally Diagonalizable Matrix Example orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. E x e is also symmetric because ðe x eñ. an \(n\times n\) matrix \(a\) is diagonalizable if and only if. Orthogonally Diagonalizable Matrix Example.
From semath.info
How to diagonalize a 3x3 matrix Example SEMATH INFO Orthogonally Diagonalizable Matrix Example an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly. \(a\) is orthogonally diagonalizable. E x e is also symmetric because ðe x eñ. So any real symmetric matrix is orthogonally diagonalizable. We have seen. Orthogonally Diagonalizable Matrix Example.
From apniphysics.com
Types of Matrices Examples of Matrices Types For The Beginner Orthogonally Diagonalizable Matrix Example So any real symmetric matrix is orthogonally diagonalizable. orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n. Orthogonally Diagonalizable Matrix Example.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonally Diagonalizable Matrix Example We have seen examples of. in the following example, the orthogonal matrix \(u\) will be found to orthogonally diagonalize a matrix. \(a\) is orthogonally diagonalizable. An n×n n × n matrix a a is said to be orthogonally diagonalizable if there are an orthogonal matrix p p (with p −1. example if e is any matrix (square. Orthogonally Diagonalizable Matrix Example.
From moriah-has-stanton.blogspot.com
When Is a Matrix Orthogonally Diagonalizable MoriahhasStanton Orthogonally Diagonalizable Matrix Example an n nmatrix a is symmetric if and only if it is orthogonally diagonalizable. an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by \[p=\left[\begin{array}{cccc} x_{1} &. orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. An n×n n. Orthogonally Diagonalizable Matrix Example.