Geometric Mean In Similar Right Triangles Legs . theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. The projection of a leg is. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric. geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. how to use the leg geometric mean theorem. The geometric mean theorem (or altitude theorem) states that the altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle. the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse.
from www.chegg.com
in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric. how to use the leg geometric mean theorem. The geometric mean theorem (or altitude theorem) states that the altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle. The projection of a leg is. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse.
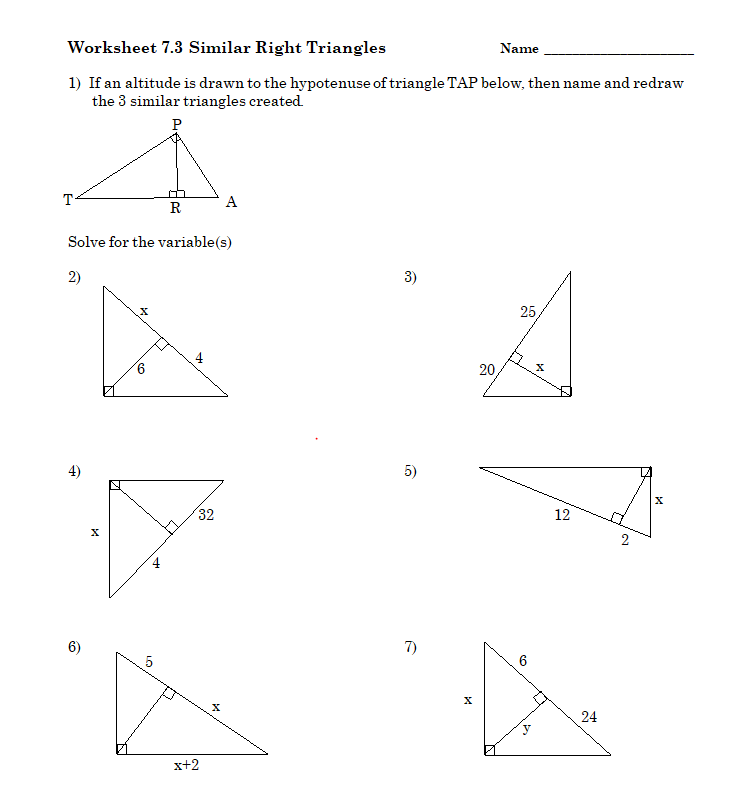
Solved Worksheet 7.3 Similar Right Triangles Name 1) If an
Geometric Mean In Similar Right Triangles Legs the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. how to use the leg geometric mean theorem. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is. The projection of a leg is. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric. The geometric mean theorem (or altitude theorem) states that the altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle.
From www.ck12.org
SAS Similarity ( Read ) Geometry CK12 Foundation Geometric Mean In Similar Right Triangles Legs the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment. Geometric Mean In Similar Right Triangles Legs.
From calcworkshop.com
Similar Right Triangles (Fully Explained w/ 9 Examples!) Geometric Mean In Similar Right Triangles Legs the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse. Geometric Mean In Similar Right Triangles Legs.
From www.youtube.com
Similarity, Right Triangles, & Trigonometry Geometric Mean (1) YouTube Geometric Mean In Similar Right Triangles Legs theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. how to use the leg geometric mean theorem. in a. Geometric Mean In Similar Right Triangles Legs.
From www.geogebra.org
Geometric Mean in Right Triangles GeoGebra Geometric Mean In Similar Right Triangles Legs in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. the leg of a right triangle is the mean proportional between the hypotenuse and. Geometric Mean In Similar Right Triangles Legs.
From www.mrseteachesmath.com
Triangle Similarity INB Pages Mrs. E Teaches Math Geometric Mean In Similar Right Triangles Legs geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length. Geometric Mean In Similar Right Triangles Legs.
From www.youtube.com
Right Triangle Geometric Mean Altitude Theorem YouTube Geometric Mean In Similar Right Triangles Legs The geometric mean theorem (or altitude theorem) states that the altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle. The projection of a leg is. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a. Geometric Mean In Similar Right Triangles Legs.
From www.youtube.com
Proportional Parts of Similar Triangles YouTube Geometric Mean In Similar Right Triangles Legs the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric.. Geometric Mean In Similar Right Triangles Legs.
From www.slideserve.com
PPT 74 Similarity in Right Triangles PowerPoint Presentation, free Geometric Mean In Similar Right Triangles Legs theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. it turns out the when you drop an altitude (h in. Geometric Mean In Similar Right Triangles Legs.
From www.youtube.com
Quick Review Similar Right Triangles Finding Leg Lengths YouTube Geometric Mean In Similar Right Triangles Legs The geometric mean theorem (or altitude theorem) states that the altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle. The projection of a leg is. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the. Geometric Mean In Similar Right Triangles Legs.
From www.slideshare.net
Right Triangle Similarity Geometric Mean In Similar Right Triangles Legs how to use the leg geometric mean theorem. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. geometric mean. Geometric Mean In Similar Right Triangles Legs.
From www.media4math.com
DefinitionTriangle ConceptsLegs of a Right Triangle Media4Math Geometric Mean In Similar Right Triangles Legs geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. how to use the leg geometric mean theorem. The geometric mean theorem (or altitude theorem) states that the altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle. theorem 9.8 geometric mean. Geometric Mean In Similar Right Triangles Legs.
From brainly.com
unit 8 right triangles and trigonometry homework 3 similar right Geometric Mean In Similar Right Triangles Legs geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. how to use the leg geometric mean theorem. in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. the length of each leg of the right triangle is the geometric mean of the lengths. Geometric Mean In Similar Right Triangles Legs.
From learningmagicfebrility.z13.web.core.windows.net
Practice Questions On Similar Triangles Geometric Mean In Similar Right Triangles Legs how to use the leg geometric mean theorem. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is.. Geometric Mean In Similar Right Triangles Legs.
From www.cuemath.com
Altitude of a Triangle Definition, Formulas, Properties, Examples Geometric Mean In Similar Right Triangles Legs the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. The geometric mean theorem (or altitude theorem) states that. Geometric Mean In Similar Right Triangles Legs.
From www.mathwarehouse.com
Similar Right Triangles formed by an Altitude. The Geometric Mean is Geometric Mean In Similar Right Triangles Legs the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. theorem 9.8 geometric mean (leg) theorem in a. Geometric Mean In Similar Right Triangles Legs.
From www.slideserve.com
PPT Similar Right Triangles PowerPoint Presentation, free download Geometric Mean In Similar Right Triangles Legs the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric.. Geometric Mean In Similar Right Triangles Legs.
From www.slideserve.com
PPT 8.4 Similarity in Right Triangles PowerPoint Presentation, free Geometric Mean In Similar Right Triangles Legs in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric. The geometric mean theorem (or altitude theorem) states. Geometric Mean In Similar Right Triangles Legs.
From www.math-principles.com
Math Principles Similar Triangles, 2 Geometric Mean In Similar Right Triangles Legs The projection of a leg is. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the. Geometric Mean In Similar Right Triangles Legs.
From zipworksheet.com
Similar Right Triangles Worksheet Geometric Mean In Similar Right Triangles Legs it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. The geometric mean theorem (or. Geometric Mean In Similar Right Triangles Legs.
From www.chegg.com
Solved Worksheet 7.3 Similar Right Triangles Name 1) If an Geometric Mean In Similar Right Triangles Legs The projection of a leg is. The geometric mean theorem (or altitude theorem) states that the altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the. Geometric Mean In Similar Right Triangles Legs.
From www.slideshare.net
Right Triangle Similarity Geometric Mean In Similar Right Triangles Legs in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. how to use the leg geometric mean theorem. the leg of a right triangle is the mean proportional between the hypotenuse and the projection. Geometric Mean In Similar Right Triangles Legs.
From www.youtube.com
Similar Right Triangles Examples Using Geometric Mean Method YouTube Geometric Mean In Similar Right Triangles Legs the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. The projection of a leg is. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a. Geometric Mean In Similar Right Triangles Legs.
From learninglibcogar.z4.web.core.windows.net
Practice Similar Triangles Worksheet Geometric Mean In Similar Right Triangles Legs it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric. The projection of a leg is. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the. Geometric Mean In Similar Right Triangles Legs.
From www.showme.com
Geometry 7.3 Geomtric Mean (Leg) Theorem [Thm 7.7] Math, geometry Geometric Mean In Similar Right Triangles Legs The projection of a leg is. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude. Geometric Mean In Similar Right Triangles Legs.
From printablelibagnames.z13.web.core.windows.net
Parts Of Similar Triangles Worksheet Geometric Mean In Similar Right Triangles Legs the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. the length of each leg of the right triangle is the. Geometric Mean In Similar Right Triangles Legs.
From www.varsitytutors.com
How to find if right triangles are similar Basic Geometry Geometric Mean In Similar Right Triangles Legs The projection of a leg is. in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. the length of each leg of the right triangle is. Geometric Mean In Similar Right Triangles Legs.
From classcampusenrique.z19.web.core.windows.net
Proving Similar Triangles Examples Geometric Mean In Similar Right Triangles Legs how to use the leg geometric mean theorem. The projection of a leg is. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. it turns out the when you drop an altitude (h in the picture below) from the the right angle. Geometric Mean In Similar Right Triangles Legs.
From home-school-math.blogspot.com
Home School Math How To Find The Altitude Of A Right Triangle Geometric Mean In Similar Right Triangles Legs how to use the leg geometric mean theorem. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric. in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. Geometric Mean In Similar Right Triangles Legs.
From www.gauthmath.com
Solved Theorem i friangle similarity and right triangles legs. The Geometric Mean In Similar Right Triangles Legs geometric mean (or mean proportional) appears in two popular theorems regarding right triangles. the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is. The projection of a leg is. it turns out the when you drop an altitude (h in. Geometric Mean In Similar Right Triangles Legs.
From www.slideserve.com
PPT Notes Geometric Mean / Similarity in Right Triangles PowerPoint Geometric Mean In Similar Right Triangles Legs it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric. the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is.. Geometric Mean In Similar Right Triangles Legs.
From brainly.com
Unit 7 right triangles & trigonometry homework 4 trigonometry ratios Geometric Mean In Similar Right Triangles Legs The projection of a leg is. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. it turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude. Geometric Mean In Similar Right Triangles Legs.
From www.ck12.org
Inscribed Similar Triangles ( Read ) Geometry CK12 Foundation Geometric Mean In Similar Right Triangles Legs the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is. The geometric mean theorem (or altitude theorem) states that the altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle.. Geometric Mean In Similar Right Triangles Legs.
From www.youtube.com
Triangles Similar Right Triangles, Geometric Mean YouTube Geometric Mean In Similar Right Triangles Legs how to use the leg geometric mean theorem. in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. The geometric mean theorem (or altitude theorem) states that the altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original. Geometric Mean In Similar Right Triangles Legs.
From www.geogebra.org
Right Triangle Altitude Theorem GeoGebra Geometric Mean In Similar Right Triangles Legs in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. theorem 9.8 geometric mean (leg) theorem in a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two. the length of each leg of the right triangle is the geometric mean of. Geometric Mean In Similar Right Triangles Legs.
From rumble.com
Using Geometry to find the Legs and Altitude of a Right Triangle Geometric Mean In Similar Right Triangles Legs the leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse. how to use the leg geometric mean theorem. The projection of a leg is. the length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the. Geometric Mean In Similar Right Triangles Legs.