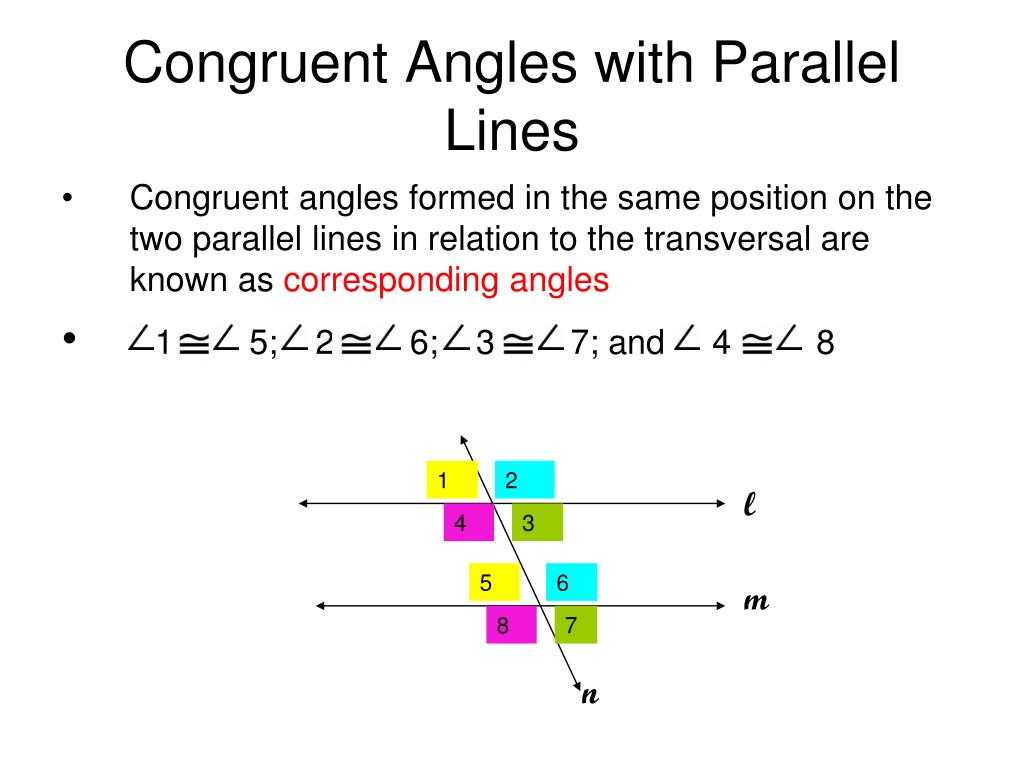
Corresponding Angles Formed By Parallel Lines Are Always Congruent . When the lines are parallel, the interior. Solve for the value of x. Corresponding angles are not always. They are interior (between the parallel lines), and they are on the same side of the transversal. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. These lines are parallel, because a pair of corresponding angles are equal. X + 20 = 3x + 9. The corresponding angles definition tells us. The corresponding angles formed by parallel lines and a transversal are always equal. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. These angles are located exactly as their name describes. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. As they are corresponding angles and the lines are said to be. Vertically opposite angles are always congruent angles.
from www.slideserve.com
These lines are parallel, because a pair of corresponding angles are equal. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. Solve for the value of x. When the lines are parallel, the interior. These angles are located exactly as their name describes. As they are corresponding angles and the lines are said to be. X + 20 = 3x + 9. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles.
PPT Parallel and Perpendicular Lines PowerPoint Presentation, free
Corresponding Angles Formed By Parallel Lines Are Always Congruent Vertically opposite angles are always congruent angles. Corresponding angles are not always. Vertically opposite angles are always congruent angles. When the lines are parallel, the interior. The corresponding angles formed by parallel lines and a transversal are always equal. Solve for the value of x. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. These angles are located exactly as their name describes. They are interior (between the parallel lines), and they are on the same side of the transversal. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. X + 20 = 3x + 9. These lines are parallel, because a pair of corresponding angles are equal. As they are corresponding angles and the lines are said to be. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. The corresponding angles definition tells us. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°.
From www.slideserve.com
PPT Angles formed by Transversal and Parallel Lines March 9, 2011 Corresponding Angles Formed By Parallel Lines Are Always Congruent The corresponding angles definition tells us. Vertically opposite angles are always congruent angles. These lines are parallel, because a pair of corresponding angles are equal. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.slideserve.com
PPT Congruent angles of parallel lines cut by a transversal Corresponding Angles Formed By Parallel Lines Are Always Congruent The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. As they are corresponding angles and the lines are said to be. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. These lines are parallel, because a pair of corresponding angles are. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.cuemath.com
Congruent Angles Cuemath Corresponding Angles Formed By Parallel Lines Are Always Congruent These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. Corresponding angles are not always. These lines are parallel, because a pair of corresponding angles are equal. These angles are located exactly as their name describes. The corresponding angles formed by parallel lines and a transversal are always equal.. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.slideserve.com
PPT Parallel and Perpendicular Lines PowerPoint Presentation, free Corresponding Angles Formed By Parallel Lines Are Always Congruent The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. When the lines are parallel, the interior. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. Vertically opposite angles are always congruent angles. The corresponding angles definition tells us. Corresponding angles are. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.ck12.org
Corresponding Angles ( Read ) Geometry CK12 Foundation Corresponding Angles Formed By Parallel Lines Are Always Congruent As they are corresponding angles and the lines are said to be. They are interior (between the parallel lines), and they are on the same side of the transversal. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. The values of two corresponding angles ∠2 = 5x + 2. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.chino.k12.ca.us
Math Support / Parallel Lines Corresponding Angles Formed By Parallel Lines Are Always Congruent Corresponding angles are not always. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. As they are corresponding angles and the lines are said to be. These lines are parallel, because a pair of corresponding angles are equal. The corresponding angles postulate states that if two parallel lines. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From socratic.org
How do you construct corresponding angles? Socratic Corresponding Angles Formed By Parallel Lines Are Always Congruent The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. Corresponding angles are not always. X + 20 = 3x + 9. These angles are located exactly as their name describes. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. Vertically opposite. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.youtube.com
Angles formed by Parallel Lines and Transversals YouTube Corresponding Angles Formed By Parallel Lines Are Always Congruent Solve for the value of x. When the lines are parallel, the interior. They are interior (between the parallel lines), and they are on the same side of the transversal. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. X + 20 = 3x + 9. The corresponding angles. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From shafqatminjae.blogspot.com
10+ Chapter 3 Parallel Lines And Transversals Answers ShafqatMinjae Corresponding Angles Formed By Parallel Lines Are Always Congruent These lines are parallel, because a pair of corresponding angles are equal. When the lines are parallel, the interior. Vertically opposite angles are always congruent angles. They are interior (between the parallel lines), and they are on the same side of the transversal. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles.. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From brainly.com
based on the pattern of the drawings which conjecture is reasonable to Corresponding Angles Formed By Parallel Lines Are Always Congruent These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. Solve for the value of x. X + 20 = 3x + 9. Corresponding angles are not always. Vertically opposite angles are. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.youtube.com
Proof If Two Lines Form Congruent Adjacent Angles, Then The Lines Are Corresponding Angles Formed By Parallel Lines Are Always Congruent They are interior (between the parallel lines), and they are on the same side of the transversal. These angles are located exactly as their name describes. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. X + 20 = 3x + 9. The corresponding angles definition tells us. The values of two. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.youtube.com
(I.34) Parallelogram opposite sides and angles are congruent, Proof Corresponding Angles Formed By Parallel Lines Are Always Congruent The corresponding angles definition tells us. Corresponding angles are not always. X + 20 = 3x + 9. These lines are parallel, because a pair of corresponding angles are equal. They are interior (between the parallel lines), and they are on the same side of the transversal. Solve for the value of x. The values of two corresponding angles ∠2. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From quizlet.com
Geometry Angle Theorems Flashcards Quizlet Corresponding Angles Formed By Parallel Lines Are Always Congruent These lines are parallel, because a pair of corresponding angles are equal. The corresponding angles formed by parallel lines and a transversal are always equal. They are interior (between the parallel lines), and they are on the same side of the transversal. When the lines are parallel, the interior. The corresponding angles postulate states that if two parallel lines are. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From donsteward.blogspot.com
MEDIAN Don Steward mathematics teaching parallel line angles Corresponding Angles Formed By Parallel Lines Are Always Congruent These angles are located exactly as their name describes. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. As they are corresponding angles and the lines are said to be. They are. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.slideserve.com
PPT Math 010 Chapter 9 Geometry Lines, figures, & triangles Corresponding Angles Formed By Parallel Lines Are Always Congruent As they are corresponding angles and the lines are said to be. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. Vertically opposite angles are always congruent angles. The corresponding angles. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From mathmonks.com
Corresponding Angles Definition & Theorem with Examples Corresponding Angles Formed By Parallel Lines Are Always Congruent Corresponding angles are not always. The corresponding angles formed by parallel lines and a transversal are always equal. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. The corresponding angles postulate. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.javatpoint.com
Corresponding Angles Definition JavaTpoint Corresponding Angles Formed By Parallel Lines Are Always Congruent By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. X + 20 = 3x + 9. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. The corresponding angles postulate states that if two parallel lines are cut by a transversal,. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From la61.weebly.com
Parallel Lines and Angles Senior Block Corresponding Angles Formed By Parallel Lines Are Always Congruent X + 20 = 3x + 9. The corresponding angles formed by parallel lines and a transversal are always equal. As they are corresponding angles and the lines are said to be. Vertically opposite angles are always congruent angles. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. The values of two. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.teachoo.com
Example 5 If a transversal intersects two lines such that Corresponding Angles Formed By Parallel Lines Are Always Congruent Corresponding angles are not always. These lines are parallel, because a pair of corresponding angles are equal. The corresponding angles formed by parallel lines and a transversal are always equal. As they are corresponding angles and the lines are said to be. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. These. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From numberdyslexia.com
Free Printable angles anchor chart for classroom[PDF] Number Dyslexia Corresponding Angles Formed By Parallel Lines Are Always Congruent These lines are parallel, because a pair of corresponding angles are equal. The corresponding angles definition tells us. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. They are interior (between the parallel lines), and they are on the same side of the transversal. Vertically opposite angles are always. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From worksheetsufertatstl.z21.web.core.windows.net
Solving Angles In Transversals Corresponding Angles Formed By Parallel Lines Are Always Congruent By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. The corresponding angles definition tells us. Corresponding angles are not always. Solve for the value of x. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. Vertically opposite angles are always congruent angles. X +. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.cazoommaths.com
Geometry Resources Geometry Worksheets Printable Teaching Resources Corresponding Angles Formed By Parallel Lines Are Always Congruent The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. They are interior (between the parallel lines), and they are on the same side of the transversal. Corresponding angles are not always. These lines are parallel, because a pair of corresponding angles are equal. X + 20 = 3x +. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From calcworkshop.com
Parallel Lines Cut by a Transversal (with 23 Examples!) Corresponding Angles Formed By Parallel Lines Are Always Congruent The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. As they are corresponding angles and the lines are said to be. These lines are parallel, because a pair of corresponding angles are equal. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x +. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From jsmithmoore.com
Angles in parallel lines worksheet Corresponding Angles Formed By Parallel Lines Are Always Congruent As they are corresponding angles and the lines are said to be. When the lines are parallel, the interior. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. These lines are parallel, because a pair of corresponding angles are equal. They are interior (between the parallel lines), and they are on the. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.ck12.org
Corresponding Angles CK12 Foundation Corresponding Angles Formed By Parallel Lines Are Always Congruent Corresponding angles are not always. These lines are parallel, because a pair of corresponding angles are equal. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. These angles are located exactly as their name describes.. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.slideserve.com
PPT Parallel Line and Angles PowerPoint Presentation, free download Corresponding Angles Formed By Parallel Lines Are Always Congruent These angles are located exactly as their name describes. The corresponding angles definition tells us. When the lines are parallel, the interior. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles.. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.youtube.com
Philfour Geometry Parallel Lines Congruent & Supplementary Angle Corresponding Angles Formed By Parallel Lines Are Always Congruent These angles are located exactly as their name describes. The corresponding angles formed by parallel lines and a transversal are always equal. They are interior (between the parallel lines), and they are on the same side of the transversal. Vertically opposite angles are always congruent angles. By this definition, angles ∠1 and ∠2 in the above figure form a pair. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.slideserve.com
PPT Angle Relationships PowerPoint Presentation, free download ID Corresponding Angles Formed By Parallel Lines Are Always Congruent As they are corresponding angles and the lines are said to be. They are interior (between the parallel lines), and they are on the same side of the transversal. The corresponding angles formed by parallel lines and a transversal are always equal. The corresponding angles definition tells us. Corresponding angles are not always. These lines are not parallel, because a. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.youtube.com
In parallel lines, alternate interior angles are always equal (Theorem Corresponding Angles Formed By Parallel Lines Are Always Congruent Vertically opposite angles are always congruent angles. The corresponding angles formed by parallel lines and a transversal are always equal. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. X + 20. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.slideserve.com
PPT Congruent angles of parallel lines cut by a transversal Corresponding Angles Formed By Parallel Lines Are Always Congruent The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. As they are corresponding angles and the lines are said to be. The corresponding angles formed by parallel lines and a transversal are always equal. These lines are not parallel, because a pair of consecutive interior angles do not add. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From mavink.com
Properties Of Corresponding Angles Corresponding Angles Formed By Parallel Lines Are Always Congruent The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. The corresponding angles formed by parallel lines and a transversal are always equal. They are interior (between the parallel lines), and they are on the same side of the transversal. These lines are parallel, because a pair of corresponding angles are equal. The. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From mathsux.org
Transversals and Parallel Lines Geometry MathSux^2 Corresponding Angles Formed By Parallel Lines Are Always Congruent Solve for the value of x. The corresponding angles formed by parallel lines and a transversal are always equal. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. The values of. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.gauthmath.com
Solved if ∠ 1≌ ∠ 2 , can you conclude that any of the lines are Corresponding Angles Formed By Parallel Lines Are Always Congruent The corresponding angles formed by parallel lines and a transversal are always equal. X + 20 = 3x + 9. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x + 10. These lines are parallel, because a pair of corresponding angles are equal. These angles are located exactly as their name describes. They are. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From 7bnumbers.blogspot.com
Line and Angles Blog 3 Corresponding Angles Formed By Parallel Lines Are Always Congruent By this definition, angles ∠1 and ∠2 in the above figure form a pair of corresponding angles. Vertically opposite angles are always congruent angles. These lines are not parallel, because a pair of consecutive interior angles do not add up to 180° (81° + 101°. The values of two corresponding angles ∠2 = 5x + 2 and ∠6 = 3x. Corresponding Angles Formed By Parallel Lines Are Always Congruent.
From www.numerade.com
SOLVED 'Two parallel lines are cut by transversal Which statements Corresponding Angles Formed By Parallel Lines Are Always Congruent Corresponding angles are not always. The corresponding angles definition tells us. X + 20 = 3x + 9. The corresponding angles postulate states that if two parallel lines are cut by a transversal, the corresponding angles are congruent. Solve for the value of x. The corresponding angles formed by parallel lines and a transversal are always equal. The values of. Corresponding Angles Formed By Parallel Lines Are Always Congruent.