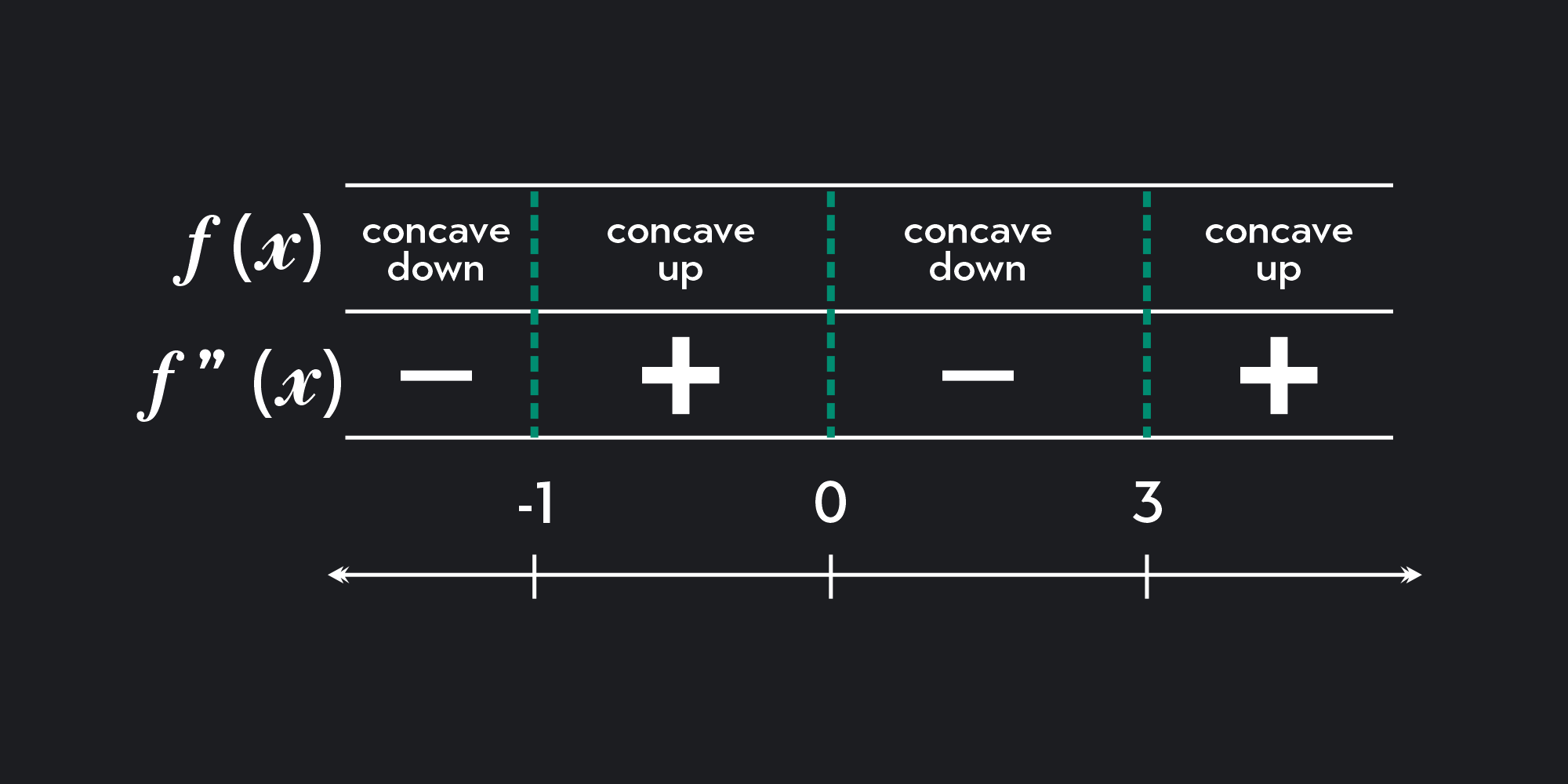
Can A Point Of Inflection Be A Local Minimum . It is certainly possible to have an inflection point that is also a (local) extreme: Concavity and points of inflection; For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. Here, $(0,0)$ is an inflection point because $f''$. This is not satisfied in the example above. An alternative is to look at the first (and possibly second). The point c is said to be a point of inflection if there exists a > 0 such that either f is convex on. The first derivative of the function must take different signed values at two sides of the local minimum point. (a;b) → r be continuous at a point c ∈ (a;b). Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. If f (3)(p) ≠ 0, then f has an inflection point at p. This is similar to an.
from articles.outlier.org
The point c is said to be a point of inflection if there exists a > 0 such that either f is convex on. The first derivative of the function must take different signed values at two sides of the local minimum point. It is certainly possible to have an inflection point that is also a (local) extreme: This is not satisfied in the example above. Here, $(0,0)$ is an inflection point because $f''$. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. (a;b) → r be continuous at a point c ∈ (a;b). If f (3)(p) ≠ 0, then f has an inflection point at p. Concavity and points of inflection; An alternative is to look at the first (and possibly second).
Inflection Point Definition and How to Find It in 5 Steps Outlier
Can A Point Of Inflection Be A Local Minimum Here, $(0,0)$ is an inflection point because $f''$. The first derivative of the function must take different signed values at two sides of the local minimum point. (a;b) → r be continuous at a point c ∈ (a;b). If f (3)(p) ≠ 0, then f has an inflection point at p. An alternative is to look at the first (and possibly second). For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. The point c is said to be a point of inflection if there exists a > 0 such that either f is convex on. It is certainly possible to have an inflection point that is also a (local) extreme: This is similar to an. Concavity and points of inflection; This is not satisfied in the example above. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. Here, $(0,0)$ is an inflection point because $f''$.
From www.wikihow.com
How to Find Inflection Points 6 Simple & Easy to Follow Steps Can A Point Of Inflection Be A Local Minimum An alternative is to look at the first (and possibly second). For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if. Can A Point Of Inflection Be A Local Minimum.
From www.savemyexams.com
Second Order Derivatives CIE IGCSE Additional Maths Revision Notes Can A Point Of Inflection Be A Local Minimum This is similar to an. The first derivative of the function must take different signed values at two sides of the local minimum point. The point c is said to be a point of inflection if there exists a > 0 such that either f is convex on. This is not satisfied in the example above. For example, take $$y(x). Can A Point Of Inflection Be A Local Minimum.
From math.stackexchange.com
calculus Can a point of local minimum be a point of inflection Can A Point Of Inflection Be A Local Minimum Here, $(0,0)$ is an inflection point because $f''$. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. If f (3)(p) ≠ 0, then f has an inflection point at p. Concavity and points of inflection; Otherwise, if f (4)(p) ≠ 0, then f has. Can A Point Of Inflection Be A Local Minimum.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Can A Point Of Inflection Be A Local Minimum The first derivative of the function must take different signed values at two sides of the local minimum point. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. An alternative is to look at the first (and possibly second). This is. Can A Point Of Inflection Be A Local Minimum.
From www.radfordmathematics.com
Point of Inflection Calculus Can A Point Of Inflection Be A Local Minimum The first derivative of the function must take different signed values at two sides of the local minimum point. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. The point c is said to be a point of inflection if there. Can A Point Of Inflection Be A Local Minimum.
From www.easysevens.com
Derivatives Local Maximum, Minimum and Point of Inflection Can A Point Of Inflection Be A Local Minimum Here, $(0,0)$ is an inflection point because $f''$. This is similar to an. This is not satisfied in the example above. The first derivative of the function must take different signed values at two sides of the local minimum point. Concavity and points of inflection; The point c is said to be a point of inflection if there exists a. Can A Point Of Inflection Be A Local Minimum.
From cs.wellesley.edu
CS112 Assignment 5 Can A Point Of Inflection Be A Local Minimum This is similar to an. It is certainly possible to have an inflection point that is also a (local) extreme: Here, $(0,0)$ is an inflection point because $f''$. If f (3)(p) ≠ 0, then f has an inflection point at p. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. The point c is said to be a point of. Can A Point Of Inflection Be A Local Minimum.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Can A Point Of Inflection Be A Local Minimum Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. If f (3)(p) ≠ 0, then f has an inflection point at p. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the. Can A Point Of Inflection Be A Local Minimum.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Can A Point Of Inflection Be A Local Minimum If f (3)(p) ≠ 0, then f has an inflection point at p. It is certainly possible to have an inflection point that is also a (local) extreme: An alternative is to look at the first (and possibly second). (a;b) → r be continuous at a point c ∈ (a;b). Here, $(0,0)$ is an inflection point because $f''$. This is. Can A Point Of Inflection Be A Local Minimum.
From real-statistics.com
Inflection Point Real Statistics Using Excel Can A Point Of Inflection Be A Local Minimum The first derivative of the function must take different signed values at two sides of the local minimum point. Here, $(0,0)$ is an inflection point because $f''$. It is certainly possible to have an inflection point that is also a (local) extreme: The point c is said to be a point of inflection if there exists a > 0 such. Can A Point Of Inflection Be A Local Minimum.
From en.neurochispas.com
Maxima, Minima and Inflection Points of Functions Neurochispas Can A Point Of Inflection Be A Local Minimum This is similar to an. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. Concavity and points of inflection; It is certainly possible to have an inflection point that is also a (local) extreme: (a;b) → r be continuous at a point c ∈ (a;b). If f (3)(p) ≠ 0, then f has an inflection point at p. The first. Can A Point Of Inflection Be A Local Minimum.
From www.numerade.com
SOLVED(a) Graph a polynomial with two local maxima and two local Can A Point Of Inflection Be A Local Minimum This is similar to an. An alternative is to look at the first (and possibly second). The first derivative of the function must take different signed values at two sides of the local minimum point. This is not satisfied in the example above. It is certainly possible to have an inflection point that is also a (local) extreme: For example,. Can A Point Of Inflection Be A Local Minimum.
From www.slideserve.com
PPT Understanding Cubic Graphs PowerPoint Presentation, free download Can A Point Of Inflection Be A Local Minimum This is not satisfied in the example above. Here, $(0,0)$ is an inflection point because $f''$. An alternative is to look at the first (and possibly second). The first derivative of the function must take different signed values at two sides of the local minimum point. The point c is said to be a point of inflection if there exists. Can A Point Of Inflection Be A Local Minimum.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Can A Point Of Inflection Be A Local Minimum For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. The first derivative of the function must take different signed values at two sides of the local minimum point. This is not satisfied in the example above. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if. Can A Point Of Inflection Be A Local Minimum.
From www.youtube.com
Calc I Local max/min, concavity and inflection points, given graph of Can A Point Of Inflection Be A Local Minimum It is certainly possible to have an inflection point that is also a (local) extreme: For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. (a;b) → r be continuous at a point c ∈ (a;b). Concavity and points of inflection; The first derivative of the function must take different signed values at two sides of the local minimum point. If. Can A Point Of Inflection Be A Local Minimum.
From www.savemyexams.com
Concavity & Points of Inflection DP IB Maths AA HL Revision Notes 2021 Can A Point Of Inflection Be A Local Minimum The point c is said to be a point of inflection if there exists a > 0 such that either f is convex on. Concavity and points of inflection; It is certainly possible to have an inflection point that is also a (local) extreme: If the partials are 0, yet the surface is not constant, and is not a maximum. Can A Point Of Inflection Be A Local Minimum.
From www.nagwa.com
Question Video Identifying the Equation of a Graph Given Its Local Can A Point Of Inflection Be A Local Minimum If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. The first derivative of the function must take different signed values at two sides of the local minimum point. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. It is certainly possible to have an. Can A Point Of Inflection Be A Local Minimum.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Can A Point Of Inflection Be A Local Minimum If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. If f (3)(p) ≠ 0, then f has an inflection point at p. This is not satisfied in the example above. It is certainly possible to. Can A Point Of Inflection Be A Local Minimum.
From www.youtube.com
Stationary points to find local max,min and stationary inflections Can A Point Of Inflection Be A Local Minimum If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. (a;b) → r be continuous at a point c ∈ (a;b). It is certainly possible to have an inflection point that is also a (local) extreme: This is not satisfied in the example above. For. Can A Point Of Inflection Be A Local Minimum.
From www.mashupmath.com
How to Graph a Function in 3 Easy Steps — Mashup Math Can A Point Of Inflection Be A Local Minimum If f (3)(p) ≠ 0, then f has an inflection point at p. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. It is certainly possible to have an inflection point that. Can A Point Of Inflection Be A Local Minimum.
From www.numerade.com
SOLVED On the graph of the function below, identify all extrema (local Can A Point Of Inflection Be A Local Minimum For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. This is not satisfied in the example above. Here, $(0,0)$ is an inflection point because $f''$. It is certainly possible to have an inflection point that is also a (local) extreme: If f (3)(p) ≠ 0, then f has an inflection point at p. The point c is said to be. Can A Point Of Inflection Be A Local Minimum.
From www.youtube.com
Part I Find the Local Max/Min Point, Inflection Points and Determine Can A Point Of Inflection Be A Local Minimum If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. It is certainly possible to have an inflection point that is also a (local) extreme: This is similar to an. (a;b) → r be continuous at a point c ∈ (a;b). An alternative is to. Can A Point Of Inflection Be A Local Minimum.
From www.chegg.com
Solved Identify the inflection points and local maxima and Can A Point Of Inflection Be A Local Minimum This is not satisfied in the example above. It is certainly possible to have an inflection point that is also a (local) extreme: (a;b) → r be continuous at a point c ∈ (a;b). If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. The. Can A Point Of Inflection Be A Local Minimum.
From www.dreamstime.com
Inflection Point on Graph of Function. Stock Vector Illustration of Can A Point Of Inflection Be A Local Minimum Here, $(0,0)$ is an inflection point because $f''$. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. This is similar to an. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the. Can A Point Of Inflection Be A Local Minimum.
From joijibsxf.blob.core.windows.net
Points Of Inflection On Second Derivative Graph at Crystal Willis blog Can A Point Of Inflection Be A Local Minimum An alternative is to look at the first (and possibly second). Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. Concavity and points of inflection; This is not satisfied in the example above. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if. Can A Point Of Inflection Be A Local Minimum.
From collegedunia.com
Inflection Point Calculus, Graph & Concavity Can A Point Of Inflection Be A Local Minimum (a;b) → r be continuous at a point c ∈ (a;b). It is certainly possible to have an inflection point that is also a (local) extreme: This is similar to an. The first derivative of the function must take different signed values at two sides of the local minimum point. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. If. Can A Point Of Inflection Be A Local Minimum.
From www.youtube.com
AB Calculus Find where Increasing and Decreasing, Concavity,and Points Can A Point Of Inflection Be A Local Minimum If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. Concavity and points of inflection; Here, $(0,0)$ is an inflection point because $f''$. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. The first derivative of the function must take different signed values at two. Can A Point Of Inflection Be A Local Minimum.
From math.stackexchange.com
real analysis Reconstructing a function from its critical points and Can A Point Of Inflection Be A Local Minimum Concavity and points of inflection; The first derivative of the function must take different signed values at two sides of the local minimum point. If f (3)(p) ≠ 0, then f has an inflection point at p. This is similar to an. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum,. Can A Point Of Inflection Be A Local Minimum.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Can A Point Of Inflection Be A Local Minimum (a;b) → r be continuous at a point c ∈ (a;b). An alternative is to look at the first (and possibly second). This is not satisfied in the example above. This is similar to an. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point.. Can A Point Of Inflection Be A Local Minimum.
From discover.hubpages.com
Calculus Made Understandable Extrema and Inflection Points HubPages Can A Point Of Inflection Be A Local Minimum Concavity and points of inflection; If f (3)(p) ≠ 0, then f has an inflection point at p. This is similar to an. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq.. Can A Point Of Inflection Be A Local Minimum.
From www.youtube.com
Optimisation in Economics Maximum and Minimum Value of a Function Can A Point Of Inflection Be A Local Minimum Concavity and points of inflection; Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. The point c is said to be a point of inflection if there exists a > 0 such that either f is convex on. For example, take. Can A Point Of Inflection Be A Local Minimum.
From www.radfordmathematics.com
Point of Inflection Calculus Can A Point Of Inflection Be A Local Minimum This is not satisfied in the example above. The first derivative of the function must take different signed values at two sides of the local minimum point. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. For example, take $$y(x) =. Can A Point Of Inflection Be A Local Minimum.
From www.showme.com
Critical points & inflection points from a graph Math ShowMe Can A Point Of Inflection Be A Local Minimum An alternative is to look at the first (and possibly second). This is similar to an. Otherwise, if f (4)(p) ≠ 0, then f has a local minimum at p if f (4)(p) > 0 and a local maximum if f (4)(p) < 0. For example, take $$y(x) = \left\{\begin{array}{ll} x^2 &\text{if }x\leq. If f (3)(p) ≠ 0, then f. Can A Point Of Inflection Be A Local Minimum.
From www.youtube.com
How to Find Local Maximum and Minimum of Piecewise Function l Critical Can A Point Of Inflection Be A Local Minimum (a;b) → r be continuous at a point c ∈ (a;b). The point c is said to be a point of inflection if there exists a > 0 such that either f is convex on. The first derivative of the function must take different signed values at two sides of the local minimum point. Concavity and points of inflection; If. Can A Point Of Inflection Be A Local Minimum.
From www.youtube.com
Critical Points Saddle Points Stationary Point and Point of Inflection Can A Point Of Inflection Be A Local Minimum Here, $(0,0)$ is an inflection point because $f''$. An alternative is to look at the first (and possibly second). If f (3)(p) ≠ 0, then f has an inflection point at p. If the partials are 0, yet the surface is not constant, and is not a maximum or minimum, the point is called a saddle point. This is similar. Can A Point Of Inflection Be A Local Minimum.