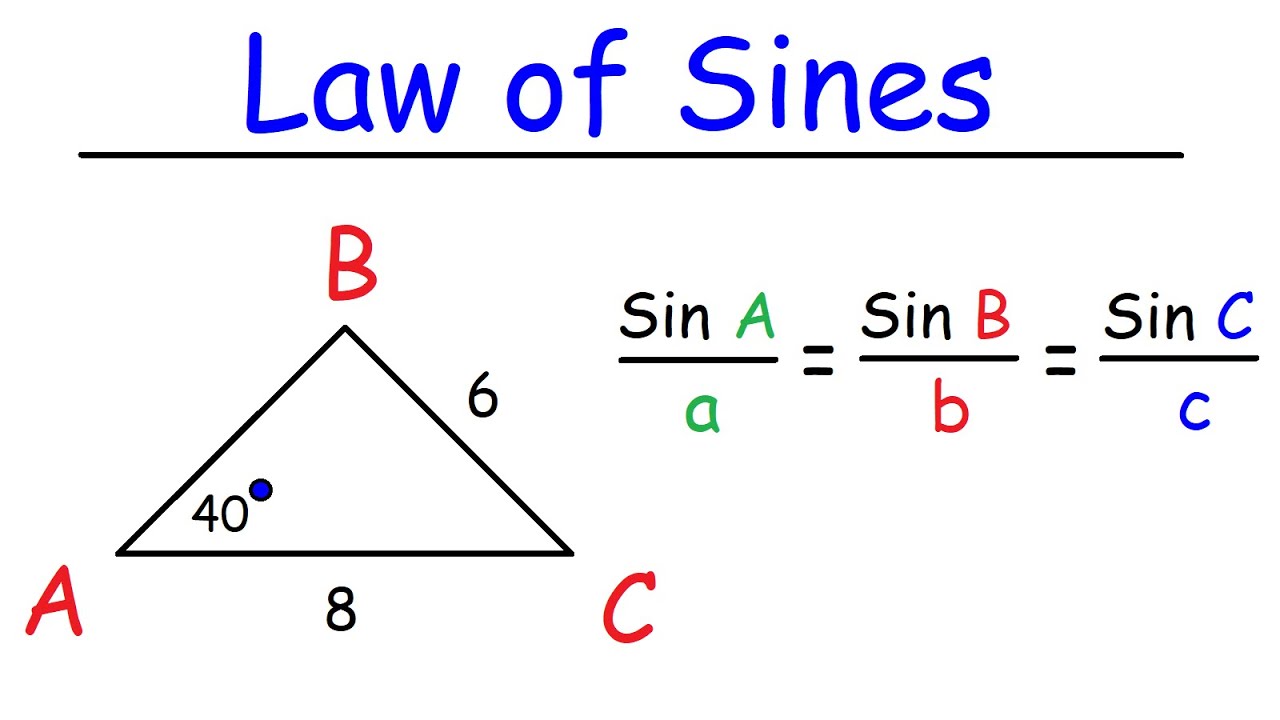
Triangle Area Formula Sine Rule . A, b and c are angles. A, b and c are sides. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any triangle the. \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. The area of any triangle can be calculated using the formula: The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The area of any triangle can be calculated using the formula: It allows us to find the. The law of sines (or sine rule) is very useful for solving triangles: A sin a = b sin b = c sin c. Areaδ = ½ ab sin c. The sine rule formula gives the ratio of the sides and angles of a triangle. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Area = ½ × base(b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. Here a, b, c are the length of the sides of the triangle, and a, b,.
from www.youtube.com
Area = ½ × base(b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. The area of any triangle can be calculated using the formula: \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. It works for any triangle: A, b and c are angles. Areaδ = ½ ab sin c. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. It allows us to find the. The law of sines (or sine rule) is very useful for solving triangles:
Law of Sines Basic Introduction YouTube
Triangle Area Formula Sine Rule A, b and c are sides. It allows us to find the. The area of any triangle can be calculated using the formula: It works for any triangle: The sine rule formula gives the ratio of the sides and angles of a triangle. Here a, b, c are the length of the sides of the triangle, and a, b,. Area = ½ × base(b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. A, b and c are angles. The law of sines (or sine rule) is very useful for solving triangles: Areaδ = ½ ab sin c. The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. A, b and c are sides. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any triangle the. The area of any triangle can be calculated using the formula:
From ronaldgokeoneal.blogspot.com
Area of Triangle Sine Rule Triangle Area Formula Sine Rule The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. The area of any triangle can be calculated using the formula: It works for any triangle: A, b and c are angles. The area of any triangle can be calculated using the formula: Here a, b, c are the. Triangle Area Formula Sine Rule.
From www.slideserve.com
PPT Sine Rule PowerPoint Presentation, free download ID5489503 Triangle Area Formula Sine Rule It allows us to find the. The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The most common formula for the area of a triangle would be: Areaδ = ½ ab sin c. Area = ½ × base(b) × height (h) another formula that can be used to obtain the area of a triangle uses. Triangle Area Formula Sine Rule.
From quizizz.com
Section 14 4 Area and The Law of Sines Quizizz Triangle Area Formula Sine Rule \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any triangle the. Here a, b, c are the length of the sides of the triangle, and a, b,. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. A, b. Triangle Area Formula Sine Rule.
From www.youtube.com
Area of a Triangle Formula Sine Formula for the Area of a Triangle Triangle Area Formula Sine Rule The law of sines (or sine rule) is very useful for solving triangles: \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. It works for any triangle: Areaδ = ½ ab sin c. The area of any triangle can be calculated using the formula: It allows us to find the. A, b and. Triangle Area Formula Sine Rule.
From www.youtube.com
The Sine Rule Area of Triangle YouTube Triangle Area Formula Sine Rule The law of sines (or sine rule) is very useful for solving triangles: The area of any triangle can be calculated using the formula: The sine rule formula gives the ratio of the sides and angles of a triangle. Areaδ = ½ ab sin c. A, b and c are angles. The sine rule can be explained using the expression,. Triangle Area Formula Sine Rule.
From thirdspacelearning.com
Sine Rule GCSE Maths Steps, Examples & Worksheet Triangle Area Formula Sine Rule It works for any triangle: The area of any triangle can be calculated using the formula: The sine rule formula gives the ratio of the sides and angles of a triangle. Here a, b, c are the length of the sides of the triangle, and a, b,. \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of. Triangle Area Formula Sine Rule.
From www.youtube.com
Maths Tutorial Trigonometry Law of Sines / Sine Rule YouTube Triangle Area Formula Sine Rule The sine rule formula gives the ratio of the sides and angles of a triangle. Areaδ = ½ ab sin c. The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The most common formula for the area of a triangle would be: It allows us to find the. \(\text{area of a triangle} = \frac{1}{2} ab. Triangle Area Formula Sine Rule.
From www.youtube.com
Sine Rule for the Area of a Triangle YouTube Triangle Area Formula Sine Rule A, b and c are angles. The area of any triangle can be calculated using the formula: A, b and c are sides. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. It allows us to find the. Areaδ = ½ ab sin c. Area = ½ ×. Triangle Area Formula Sine Rule.
From nickolasknoeroy.blogspot.com
Area of Triangle Sine Rule NickolasknoeRoy Triangle Area Formula Sine Rule Area = ½ × base(b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. It allows us to find the. It works for any triangle: The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The area of any triangle can be calculated using the. Triangle Area Formula Sine Rule.
From www.youtube.com
Sine rule complete proof Law of sines Properties of Triangles Triangle Area Formula Sine Rule A, b and c are sides. Here a, b, c are the length of the sides of the triangle, and a, b,. Areaδ = ½ ab sin c. It allows us to find the. A sin a = b sin b = c sin c. A, b and c are angles. The sine rule formula gives the ratio of the. Triangle Area Formula Sine Rule.
From corbettmaths.com
Area of a Triangle Sine Video Corbettmaths Triangle Area Formula Sine Rule A sin a = b sin b = c sin c. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any triangle the. A, b and c are sides. The sine rule formula gives the ratio of the sides and angles of a triangle. The most common formula for the area. Triangle Area Formula Sine Rule.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Area Formula Sine Rule The law of sines (or sine rule) is very useful for solving triangles: A, b and c are angles. Areaδ = ½ ab sin c. The area of any triangle can be calculated using the formula: It allows us to find the. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of. Triangle Area Formula Sine Rule.
From cevtiwik.blob.core.windows.net
Triangle Sine Equation at Elaine Findley blog Triangle Area Formula Sine Rule The area of any triangle can be calculated using the formula: The sine rule formula gives the ratio of the sides and angles of a triangle. A, b and c are angles. A, b and c are sides. The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The area of any triangle can be calculated. Triangle Area Formula Sine Rule.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Owlcation Triangle Area Formula Sine Rule The sine rule formula gives the ratio of the sides and angles of a triangle. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any triangle the. It allows us to find the. The area of a triangle can be expressed using the lengths of two sides and the sine of. Triangle Area Formula Sine Rule.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Area Formula Sine Rule The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Area = ½ × base(b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. Areaδ = ½ ab sin c. The law of sines (or sine rule) is. Triangle Area Formula Sine Rule.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras Triangle Area Formula Sine Rule The sine rule formula gives the ratio of the sides and angles of a triangle. A sin a = b sin b = c sin c. A, b and c are angles. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. It works for any triangle: \(\text{area of. Triangle Area Formula Sine Rule.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Area Formula Sine Rule A, b and c are angles. \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. Areaδ = ½ ab sin c. It allows us to find the. The most common formula for the area of a triangle would be: A, b and c are sides. The sine rule formula gives the ratio of. Triangle Area Formula Sine Rule.
From www.youtube.com
Area of a Triangle Using ½absinC Advanced Trigonometry (8/8 Triangle Area Formula Sine Rule Here a, b, c are the length of the sides of the triangle, and a, b,. Areaδ = ½ ab sin c. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any triangle the. The law of sines (or sine rule) is very useful for solving triangles: The area of any. Triangle Area Formula Sine Rule.
From www.slideserve.com
PPT The Sine Rule. PowerPoint Presentation, free download ID5357763 Triangle Area Formula Sine Rule The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Area = ½ × base(b) × height (h) another. Triangle Area Formula Sine Rule.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Area Formula Sine Rule A, b and c are sides. It allows us to find the. Here a, b, c are the length of the sides of the triangle, and a, b,. The most common formula for the area of a triangle would be: The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The sine rule formula gives the. Triangle Area Formula Sine Rule.
From www.slideshare.net
Sine rule Triangle Area Formula Sine Rule \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. The sine rule formula gives the ratio of the sides and angles of a triangle. It allows us to find the. A sin a = b sin b = c sin c. The area of a triangle can be expressed using the lengths of. Triangle Area Formula Sine Rule.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Area Formula Sine Rule The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. It works for any triangle: The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. Here a, b, c are the length of the sides of the triangle, and a, b,. Area = ½ ×. Triangle Area Formula Sine Rule.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras Triangle Area Formula Sine Rule The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any triangle the. \(\text{area of a triangle}. Triangle Area Formula Sine Rule.
From www.youtube.com
Finding the Area of a Triangle (Using Sine) YouTube Triangle Area Formula Sine Rule \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. The law of sines (or sine rule) is very useful for solving triangles: A sin a = b sin b = c sin c. The area of any triangle can be calculated using the formula: The area of a triangle can be expressed using. Triangle Area Formula Sine Rule.
From www.slideserve.com
PPT Sine Rule for Angles PowerPoint Presentation, free download ID Triangle Area Formula Sine Rule Areaδ = ½ ab sin c. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. The sine rule formula gives the ratio of the sides and angles of a triangle. \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. \ (\text. Triangle Area Formula Sine Rule.
From thirdspacelearning.com
Area of a Triangle Trig GCSE Maths Steps, Examples & Worksheet Triangle Area Formula Sine Rule \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any triangle the. A, b and c are angles. The sine rule formula gives the ratio of the sides and angles of a triangle. A, b and c are sides. Here a, b, c are the length of the sides of the. Triangle Area Formula Sine Rule.
From nickolasknoeroy.blogspot.com
Area of Triangle Sine Rule NickolasknoeRoy Triangle Area Formula Sine Rule \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. A, b and c are sides. The area of any triangle can be calculated using the formula: The law of sines (or sine rule) is very useful for solving triangles: Areaδ = ½ ab sin c. The area of any triangle can be calculated. Triangle Area Formula Sine Rule.
From www.youtube.com
Law of Sines Basic Introduction YouTube Triangle Area Formula Sine Rule \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. The area of any triangle can be calculated using the formula: The law of sines (or sine rule) is very useful for solving triangles: The sine rule formula gives the ratio of the sides and angles of a triangle. The area of any triangle. Triangle Area Formula Sine Rule.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Area Formula Sine Rule The area of any triangle can be calculated using the formula: Here a, b, c are the length of the sides of the triangle, and a, b,. The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The area of any triangle can be calculated using the formula: The sine rule formula gives the ratio of. Triangle Area Formula Sine Rule.
From bossmaths.com
G23a Area of a triangle using sine Triangle Area Formula Sine Rule The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. A, b and c are sides. The most common formula for the area of a triangle would be: The area of any triangle can be calculated using the formula: The area of any triangle can be calculated using the formula: It works for any triangle: \(\text{area. Triangle Area Formula Sine Rule.
From fullwallpaper.neocities.org
Area Of Triangle Sine Rule Triangle Area Formula Sine Rule The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The law of sines (or sine rule) is very useful for solving triangles: A sin a = b sin b = c sin c. It works for any triangle: Here a, b, c are the length of the sides of the triangle, and a, b,. A,. Triangle Area Formula Sine Rule.
From www.slideshare.net
11 X1 T04 05 sine rule (2010) Triangle Area Formula Sine Rule It works for any triangle: Here a, b, c are the length of the sides of the triangle, and a, b,. A, b and c are angles. The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. The most common formula for the area of a triangle would be: Areaδ = ½ ab sin c. Area. Triangle Area Formula Sine Rule.
From www.youtube.com
Example Determine the Area of a Triangle Using the Sine Function YouTube Triangle Area Formula Sine Rule A sin a = b sin b = c sin c. A, b and c are sides. The sine rule can be explained using the expression, a/sina = b/sinb = c/sinc. \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. The area of a triangle can be expressed using the lengths of two. Triangle Area Formula Sine Rule.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Area Formula Sine Rule Here a, b, c are the length of the sides of the triangle, and a, b,. The most common formula for the area of a triangle would be: The sine rule formula gives the ratio of the sides and angles of a triangle. Areaδ = ½ ab sin c. The law of sines (or sine rule) is very useful for. Triangle Area Formula Sine Rule.
From www.vecteezy.com
The area of triangle using sine. Editable vector EPS10 10854289 Vector Triangle Area Formula Sine Rule \(\text{area of a triangle} = \frac{1}{2} ab \sin{c}\) to calculate the area of any triangle the. Here a, b, c are the length of the sides of the triangle, and a, b,. A, b and c are sides. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. A,. Triangle Area Formula Sine Rule.