Sheaves Category Theory . The presheaf of continuous functions on x is a sheaf. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. there are several ways to build up sheaf theory with di erent axioms; taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. We introduce the basics of. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. However, some of the axioms are a little bit hard to. Sheaf theory requires some category theory, as summarized in appendix a. (picture of functions on two open subsets of an.
from ifunny.co
We introduce the basics of. Sheaf theory requires some category theory, as summarized in appendix a. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. there are several ways to build up sheaf theory with di erent axioms; The presheaf of continuous functions on x is a sheaf. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. (picture of functions on two open subsets of an. taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. However, some of the axioms are a little bit hard to.
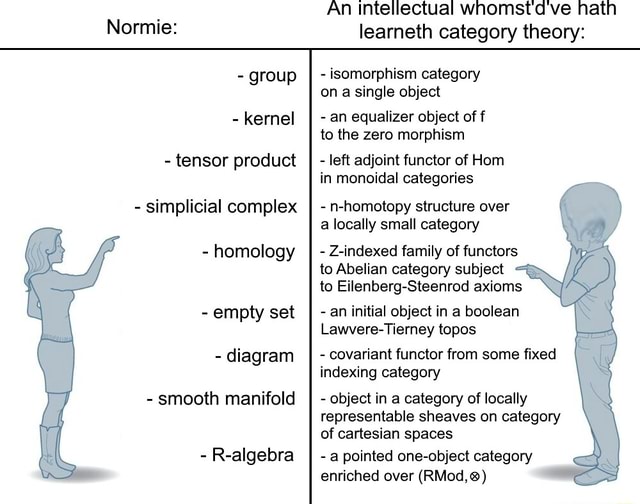
Normie group kernel tensor product simplicial complex
Sheaves Category Theory (picture of functions on two open subsets of an. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. The presheaf of continuous functions on x is a sheaf. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. We introduce the basics of. However, some of the axioms are a little bit hard to. there are several ways to build up sheaf theory with di erent axioms; sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. (picture of functions on two open subsets of an. Sheaf theory requires some category theory, as summarized in appendix a.
From www.semanticscholar.org
Figure 1 from On derived equivalences of categories of sheaves over Sheaves Category Theory However, some of the axioms are a little bit hard to. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. (picture of functions on two open subsets of an. Sheaf theory requires some category. Sheaves Category Theory.
From www.youtube.com
Presheaves and Sheaves YouTube Sheaves Category Theory taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. However, some of the axioms are a little bit hard to. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. there are several ways to build up sheaf theory with di erent axioms; Sheaf. Sheaves Category Theory.
From dokumen.tips
(PDF) Chapter 1 Sheaf theory Queen's UChapter 1 Sheaf theory The Sheaves Category Theory these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. Sheaf theory requires some category theory, as summarized in appendix a. (picture of functions on two open subsets of an. there are several ways to build up sheaf theory with di erent axioms; However, some of the axioms are a little. Sheaves Category Theory.
From www.researchgate.net
(PDF) Absolute Purity in The Category of Quasi Coherent Sheaves Sheaves Category Theory However, some of the axioms are a little bit hard to. there are several ways to build up sheaf theory with di erent axioms; (picture of functions on two open subsets of an. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. taking an applied category theory perspective,. Sheaves Category Theory.
From bookstore.ams.org
Perverse Sheaves and Applications to Representation Theory Sheaves Category Theory (picture of functions on two open subsets of an. However, some of the axioms are a little bit hard to. there are several ways to build up sheaf theory with di erent axioms; The presheaf of continuous functions on x is a sheaf. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces.. Sheaves Category Theory.
From exovwpszu.blob.core.windows.net
Sheaves With Examples at Anneliese Findlay blog Sheaves Category Theory Sheaf theory requires some category theory, as summarized in appendix a. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. there are several ways to build up sheaf theory with di erent axioms; However, some of the axioms are a little bit hard to. We introduce the basics of. these notes. Sheaves Category Theory.
From connectedpicture.blogspot.com
The Connected Picture 2017 Sheaves Category Theory (picture of functions on two open subsets of an. We introduce the basics of. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. However, some of the axioms are a little bit hard to. Sheaf theory requires some category theory, as summarized in appendix a. taking an applied category theory. Sheaves Category Theory.
From dokumen.tips
(PDF) PERVERSE SHEAVES OF CATEGORIES AND NONRATIONALITY · 2. Perverse Sheaves Category Theory We introduce the basics of. The presheaf of continuous functions on x is a sheaf. (picture of functions on two open subsets of an. there are several ways to build up sheaf theory with di erent axioms; Sheaf theory requires some category theory, as summarized in appendix a. taking an applied category theory perspective, sheaf theory through examples. Sheaves Category Theory.
From math.stackexchange.com
category theory Construction of gluing sheaves as an equaliser Sheaves Category Theory taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. We introduce the basics of. However, some. Sheaves Category Theory.
From ifunny.co
Normie group kernel tensor product simplicial complex Sheaves Category Theory there are several ways to build up sheaf theory with di erent axioms; (picture of functions on two open subsets of an. taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. Sheaf theory requires some category theory, as summarized in appendix a. these notes are for a seminar run by david. Sheaves Category Theory.
From math.stackexchange.com
sheaf theory Homological algebra and sheaves Mathematics Stack Exchange Sheaves Category Theory The presheaf of continuous functions on x is a sheaf. We introduce the basics of. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. Sheaf theory requires some category theory, as summarized in appendix a. —. Sheaves Category Theory.
From www.scribd.com
GL (2) Over Cohomology of Compactified Manifolds of Modules of Sheaves Category Theory taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. Sheaf theory requires some category theory, as summarized in appendix a. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. (picture of functions on two open subsets of an. these notes are for. Sheaves Category Theory.
From connectedpicture.blogspot.com
The Connected Picture 2017 Sheaves Category Theory Sheaf theory requires some category theory, as summarized in appendix a. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. However, some of the axioms are a little bit hard to. taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. sheaf theory is. Sheaves Category Theory.
From www.youtube.com
Justin Curry (05/18/2022) Exemplars of Sheaf Theory in TDA YouTube Sheaves Category Theory However, some of the axioms are a little bit hard to. The presheaf of continuous functions on x is a sheaf. there are several ways to build up sheaf theory with di erent axioms; (picture of functions on two open subsets of an. Sheaf theory requires some category theory, as summarized in appendix a. We introduce the basics of.. Sheaves Category Theory.
From deepai.org
Recursion and Sequentiality in Categories of Sheaves DeepAI Sheaves Category Theory sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. Sheaf theory requires some category theory, as summarized in appendix a. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. However, some of the axioms are a little bit hard to. The presheaf of. Sheaves Category Theory.
From www.cambridge.org
The Theory of Sheaves. By Richard G. Swan. Chicago lectures in Sheaves Category Theory However, some of the axioms are a little bit hard to. We introduce the basics of. taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. — this book provides an inviting tour through sheaf. Sheaves Category Theory.
From studylib.net
EXPLICIT METHODS FOR DERIVED CATEGORIES OF SHEAVES Sheaves Category Theory sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. The presheaf of continuous functions on x is a sheaf. We introduce the basics of. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. there are several ways to build up sheaf theory with. Sheaves Category Theory.
From www.amazon.com
Categories and Sheaves (Grundlehren der mathematischen Wissenschaften Sheaves Category Theory Sheaf theory requires some category theory, as summarized in appendix a. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. We introduce the basics of. (picture of functions on two open subsets of an. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces.. Sheaves Category Theory.
From www.researchgate.net
(PDF) Perverse sheaves of categories and some applications Sheaves Category Theory sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. Sheaf theory requires some category theory, as summarized in appendix a. The presheaf of continuous functions on x is a sheaf. However, some of the axioms are a little bit hard to. We introduce the basics of. — this book provides an inviting. Sheaves Category Theory.
From mathoverflow.net
ag.algebraic geometry Physical interpretations/meanings of the notion Sheaves Category Theory these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. Sheaf theory requires some category theory, as summarized in appendix a. taking an applied category theory perspective, sheaf theory through examples provides. Sheaves Category Theory.
From www.scribd.com
KRietsch Perverse Sheaves PDF Mathematical Concepts Category Theory Sheaves Category Theory sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. However, some of the axioms are a little bit. Sheaves Category Theory.
From www.scribd.com
Modules over Projective Schemes Defining Sheaves of Modules on Sheaves Category Theory taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. Sheaf theory requires some category theory, as summarized in appendix a. (picture of functions on two open subsets of an. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. — this book provides an. Sheaves Category Theory.
From www.scribd.com
Sheaves in Elementary Mathematics PDF Category Theory Abstract Sheaves Category Theory (picture of functions on two open subsets of an. there are several ways to build up sheaf theory with di erent axioms; However, some of the axioms are a little bit hard to. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. The presheaf of continuous functions on x is a sheaf.. Sheaves Category Theory.
From www.scribd.com
Categories and Sheaves PDF PDF Functions And Mappings Sheaves Category Theory there are several ways to build up sheaf theory with di erent axioms; We introduce the basics of. (picture of functions on two open subsets of an. Sheaf theory requires some category theory, as summarized in appendix a. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. However, some of. Sheaves Category Theory.
From www.weltbild.de
Exact Categories and Categories of Sheaves Buch versandkostenfrei Sheaves Category Theory Sheaf theory requires some category theory, as summarized in appendix a. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. However, some of the axioms are a little bit hard to. The presheaf of continuous functions on x is a sheaf. We introduce the basics of. these notes are. Sheaves Category Theory.
From www.scribd.com
Complex Systems From The Perspective of Category Theory 2 Covering Sheaves Category Theory there are several ways to build up sheaf theory with di erent axioms; these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. We introduce the basics of. taking an applied. Sheaves Category Theory.
From www.researchgate.net
(PDF) Purity in categories of sheaves Sheaves Category Theory The presheaf of continuous functions on x is a sheaf. there are several ways to build up sheaf theory with di erent axioms; taking an applied category theory perspective, sheaf theory through examples provides an approachable introduction to. However, some of the axioms are a little bit hard to. — this book provides an inviting tour through. Sheaves Category Theory.
From math.stackexchange.com
differential geometry Why do the ideas in Sheaf theory seem analogous Sheaves Category Theory there are several ways to build up sheaf theory with di erent axioms; However, some of the axioms are a little bit hard to. (picture of functions on two open subsets of an. The presheaf of continuous functions on x is a sheaf. We introduce the basics of. sheaf theory is the mathematical tool to treat the familiar. Sheaves Category Theory.
From www.youtube.com
Sheaf (mathematics) YouTube Sheaves Category Theory there are several ways to build up sheaf theory with di erent axioms; However, some of the axioms are a little bit hard to. — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. these notes are for a seminar run by david nadler on derived symplectic geometry in. Sheaves Category Theory.
From matematiflo.github.io
Matematiflo Sheaves Category Theory these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. We introduce the basics of. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. However, some of the axioms are a little bit hard to. (picture of functions on two open subsets of an. Sheaf. Sheaves Category Theory.
From math.stackexchange.com
category theory How do you derive the adjoint's "naturality Sheaves Category Theory sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. (picture of functions on two open subsets of an. The presheaf of continuous functions on x is a sheaf. We introduce the basics of. However, some of the axioms are a little bit hard to. — this book provides an inviting tour through. Sheaves Category Theory.
From www.researchgate.net
(PDF) Derived categories of coherent sheaves and equivalences between them Sheaves Category Theory there are several ways to build up sheaf theory with di erent axioms; (picture of functions on two open subsets of an. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. The presheaf of continuous functions on x is a sheaf. taking an applied category theory perspective, sheaf theory. Sheaves Category Theory.
From www.cambridge.org
Sheaves and sheaf spaces (Chapter 2) Sheaf Theory Sheaves Category Theory — this book provides an inviting tour through sheaf theory, from the perspective of applied category theory and. sheaf theory is the mathematical tool to treat the familiar local/global dichotomy on topological spaces. (picture of functions on two open subsets of an. We introduce the basics of. there are several ways to build up sheaf theory with. Sheaves Category Theory.
From www.researchgate.net
(PDF) Derived category of coherent sheaves and counting invariants Sheaves Category Theory The presheaf of continuous functions on x is a sheaf. We introduce the basics of. (picture of functions on two open subsets of an. However, some of the axioms are a little bit hard to. these notes are for a seminar run by david nadler on derived symplectic geometry in fall 2021. — this book provides an inviting. Sheaves Category Theory.
From vdoc.pub
Sheaves And Homotopy Theory [expository Notes] [PDF] [41u51s5c5eg0] Sheaves Category Theory Sheaf theory requires some category theory, as summarized in appendix a. We introduce the basics of. (picture of functions on two open subsets of an. The presheaf of continuous functions on x is a sheaf. However, some of the axioms are a little bit hard to. — this book provides an inviting tour through sheaf theory, from the perspective. Sheaves Category Theory.