Equalizer Category Theory . An equalizer is a map that makes two other maps equal in a category. We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). An equalizer is a limit. However, note that the equaliser is not the only set that. \delta(\lim f) \to f)\) of \(f\). Learn the properties, constructions, and applications of equalizers in. Learn how to define and use equalizers and pullbacks in category theory, with intuitive explanations and diagrams. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. Equalizers are the category analogue of sets with equal. An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. Let \(\cc\) be a category, and suppose \(e:
from wiki.gnuradio.org
\delta(\lim f) \to f)\) of \(f\). Let \(\cc\) be a category, and suppose \(e: Equalizers are the category analogue of sets with equal. However, note that the equaliser is not the only set that. An equalizer is a map that makes two other maps equal in a category. Learn the properties, constructions, and applications of equalizers in. An equalizer is a limit. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples.
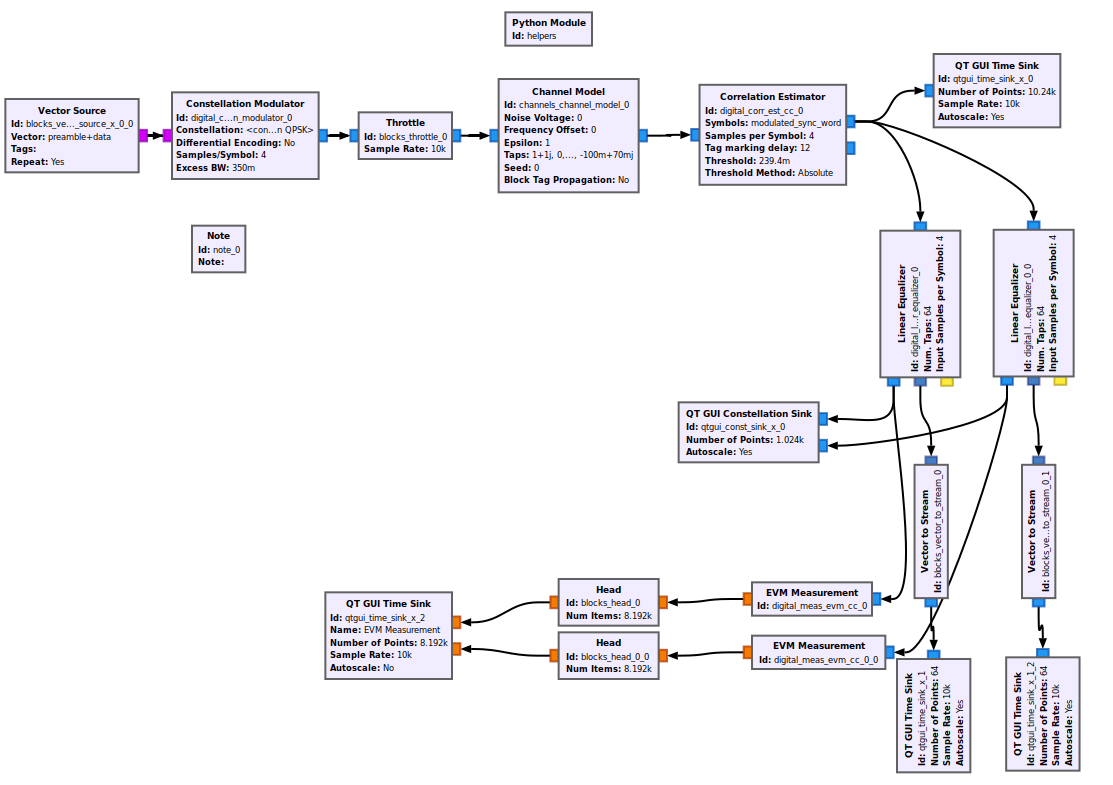
Linear Equalizer GNU Radio
Equalizer Category Theory An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: \delta(\lim f) \to f)\) of \(f\). An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : Learn the properties, constructions, and applications of equalizers in. Equalizers are the category analogue of sets with equal. Learn how to define and use equalizers and pullbacks in category theory, with intuitive explanations and diagrams. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). However, note that the equaliser is not the only set that. Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. An equalizer is a map that makes two other maps equal in a category. Let \(\cc\) be a category, and suppose \(e: An equalizer is a limit.
From www.diagramboard.com
parametrischer equalizer schematic Diagram Board Equalizer Category Theory An equalizer is a limit. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. Learn the properties, constructions, and applications of equalizers in. We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: Let. Equalizer Category Theory.
From circuits-audio.blogspot.com
4 Band Equalizer schematic diagram Free electronic circuit diagrams Equalizer Category Theory An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : An equalizer is a map that makes two other maps equal in a category. Let \(\cc\) be a category, and suppose \(e: Equalizers are the category analogue of sets with equal. A chapter from a book series on compact textbooks. Equalizer Category Theory.
From collider.com
'The Equalizer' Gave Us One of David Harbour's Most Intriguing Roles Equalizer Category Theory An equalizer is a limit. Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. Equalizers are the category analogue of sets with equal. Learn the properties, constructions, and applications of equalizers in. An equalizer is a map that makes two other maps equal in a category. First, the equalizer satis es the property that it is a subset. Equalizer Category Theory.
From wiki.gnuradio.org
Decision Feedback Equalizer GNU Radio Equalizer Category Theory We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: Learn how to define and use equalizers and pullbacks in category theory, with intuitive explanations and diagrams. Equalizers are the category analogue of sets with equal. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x).. Equalizer Category Theory.
From www.slideserve.com
PPT Project V Digital Signal Processing System Design Final project Guitar Effects Equalizer Category Theory Let \(\cc\) be a category, and suppose \(e: Learn the properties, constructions, and applications of equalizers in. Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. Equalizers are the category analogue of sets with equal. We define the. Equalizer Category Theory.
From slidemodel.com
Spectrum PowerPoint Equalizer Bars Slide SlideModel Equalizer Category Theory An equalizer is a limit. Learn the properties, constructions, and applications of equalizers in. Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. An equalizer is a map that makes two other maps equal in a category. An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : Equalizers. Equalizer Category Theory.
From pngset.com
Equalizer Category Theory, Gray, World Of Warcraft Transparent Png Equalizer Category Theory Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). Let \(\cc\) be a category, and suppose \(e: Learn the properties, constructions, and applications of equalizers in. Learn how to define and use equalizers and pullbacks in category theory,. Equalizer Category Theory.
From pngset.com
Equalizer Category Theory, Gray, World Of Warcraft Transparent Png Equalizer Category Theory Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. Learn the properties, constructions, and applications of equalizers in. An equalizer is a limit. Learn how to define and use equalizers and pullbacks in category theory, with intuitive explanations and diagrams. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x). Equalizer Category Theory.
From userlibraryheike.z19.web.core.windows.net
3 Band Equalizer Circuit Diagram Equalizer Category Theory Learn the properties, constructions, and applications of equalizers in. Equalizers are the category analogue of sets with equal. Let \(\cc\) be a category, and suppose \(e: Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. We define the. Equalizer Category Theory.
From www.puremix.net
Equalizer Strategy & Philosophy Equalizer Category Theory An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : However, note that the equaliser is not the only set that. Let \(\cc\) be a category, and suppose \(e: We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: \delta(\lim f) \to f)\) of \(f\). A. Equalizer Category Theory.
From electronicepedia.blogspot.com
10Band Equalizer Equalizer Category Theory Equalizers are the category analogue of sets with equal. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). Learn the properties, constructions, and applications of equalizers in. An equaliser. Equalizer Category Theory.
From tailieuelectronicprojects.blogspot.com
ELECTRONIC PROJECTS 10 Channel Equalizer using 4558 IC Equalizer Category Theory However, note that the equaliser is not the only set that. Let \(\cc\) be a category, and suppose \(e: Equalizers are the category analogue of sets with equal. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). An equalizer is a limit. \delta(\lim f) \to f)\) of \(f\). A. Equalizer Category Theory.
From www.slideserve.com
PPT IFF Category Theory Ontology PowerPoint Presentation, free download ID6638976 Equalizer Category Theory \delta(\lim f) \to f)\) of \(f\). We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: Learn how to define and use equalizers and pullbacks in category theory, with intuitive explanations and diagrams. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. Learn the properties,. Equalizer Category Theory.
From slidemodel.com
Graphic Equalizer Shapes for PowerPoint SlideModel Equalizer Category Theory Let \(\cc\) be a category, and suppose \(e: However, note that the equaliser is not the only set that. An equalizer is a limit. An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. Learn the properties, constructions, and. Equalizer Category Theory.
From pngset.com
Equalizer Category Theory, Gray, World Of Warcraft Transparent Png Equalizer Category Theory An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. Equalizers are the category analogue of sets with equal. Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}.. Equalizer Category Theory.
From www.dexerto.com
The Equalizer 3 has best Rotten Tomatoes score in the series Dexerto Equalizer Category Theory An equalizer is a limit. Learn the properties, constructions, and applications of equalizers in. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. \delta(\lim f) \to f)\) of \(f\). Let \(\cc\) be a category, and suppose \(e: An equaliser of two morphisms $f,g$ between the objects $x, y$ of. Equalizer Category Theory.
From www.shawnzhong.com
Category Theory Video 1 Shawn Zhong 钟万祥 Equalizer Category Theory We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: Equalizers are the category analogue of sets with equal. An equalizer is a map that makes two other maps equal in a category. \delta(\lim f) \to f)\) of \(f\). An equalizer is a limit. Learn the properties, constructions, and applications of equalizers in. A chapter from. Equalizer Category Theory.
From studylib.net
Matching theory, equalizer, and timing Equalizer Category Theory An equalizer is a limit. An equalizer is a map that makes two other maps equal in a category. Learn how to define and use equalizers and pullbacks in category theory, with intuitive explanations and diagrams. However, note that the equaliser is not the only set that. A chapter from a book series on compact textbooks in mathematics, covering the. Equalizer Category Theory.
From www.slideserve.com
PPT Chapter 3 Selecting a Process PowerPoint Presentation, free download ID2099399 Equalizer Category Theory First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). An equalizer is a limit. An equalizer is a map that makes two other maps equal in a category. Learn the properties, constructions, and applications of equalizers in. We define the equalizer of \(f\) and \(g\) to be limit \((\lim. Equalizer Category Theory.
From wiki.gnuradio.org
Linear Equalizer GNU Radio Equalizer Category Theory A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). An equaliser of two morphisms $f,g$ between the objects. Equalizer Category Theory.
From www.dukematlock.com
Understanding the Four Domains of EQ Duke Matlock Executive Coach Equalizer Category Theory \delta(\lim f) \to f)\) of \(f\). We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: Learn the properties, constructions, and applications of equalizers in. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. First, the equalizer satis es the property that it is a. Equalizer Category Theory.
From www.wiringdraw.com
Parametric Equalizer Circuit Diagram Equalizer Category Theory An equalizer is a map that makes two other maps equal in a category. A chapter from a book series on compact textbooks in mathematics, covering the main notions of category theory with examples. Equalizers are the category analogue of sets with equal. \delta(\lim f) \to f)\) of \(f\). Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}.. Equalizer Category Theory.
From emsleadershipacademy.com
5 Tips to Improve Your EMS Leadership EQ (Emotional Intelligence) EMS Leadership Academy Equalizer Category Theory An equalizer is a map that makes two other maps equal in a category. An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : Learn the properties, constructions, and applications of equalizers in. However, note that the equaliser is not the only set that. Let \(\cc\) be a category, and. Equalizer Category Theory.
From math.stackexchange.com
Meaning of "universal" in category theory (equalizer definition) Mathematics Stack Exchange Equalizer Category Theory First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : However, note that the equaliser is not the only set that. Learn how to define and use equalizers and pullbacks. Equalizer Category Theory.
From wiki.gnuradio.org
Linear Equalizer GNU Radio Equalizer Category Theory \delta(\lim f) \to f)\) of \(f\). First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e :. Equalizer Category Theory.
From www.toughtones.com
What Are the Frequencies on an Equalizer? (The Easy Approach Guide) Equalizer Category Theory An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : An equalizer is a limit. Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). Let \(\cc\) be a. Equalizer Category Theory.
From www.slideserve.com
PPT Equalization, Diversity, and Channel Coding PowerPoint Presentation ID708509 Equalizer Category Theory Learn the properties, constructions, and applications of equalizers in. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). Learn how to define and use equalizers and pullbacks in category theory, with intuitive explanations and diagrams. Let \(\cc\) be a category, and suppose \(e: Equalizers are the category analogue of. Equalizer Category Theory.
From dsp.stackexchange.com
digital communications decision feedback equalizer building blocks (from Adaptive Filters Equalizer Category Theory \delta(\lim f) \to f)\) of \(f\). First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). Learn the properties, constructions, and applications of equalizers in. An equalizer is a limit. Let \(\cc\) be a category, and suppose \(e: Equalizers are the category analogue of sets with equal. We define the. Equalizer Category Theory.
From math.stackexchange.com
category theory Any small limit in Set may be expressed as an equalizer of a pair of maps Equalizer Category Theory Equalizers are the category analogue of sets with equal. However, note that the equaliser is not the only set that. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x) = g(x). An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e :. Equalizer Category Theory.
From eitrainingcompany.com
Take the EQi 2.0/EQ 360 The Emotional Intelligence Training Company, Inc. Equalizer Category Theory Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. Let \(\cc\) be a category, and suppose \(e: \delta(\lim f) \to f)\) of \(f\). An equalizer is a limit. However, note that the equaliser is not the only set that. An equalizer is a map that makes two other maps equal in a category. We define the equalizer of. Equalizer Category Theory.
From www.izotope.com
Equalization (EQ) Tips & Tutorials Equalizer Category Theory Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. Equalizers are the category analogue of sets with equal. Learn how to define and use equalizers and pullbacks in category theory, with intuitive explanations and diagrams. An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : Learn the properties,. Equalizer Category Theory.
From math.stackexchange.com
category theory Proving the following is a equalizer by proving factorization for 1 implies Equalizer Category Theory \delta(\lim f) \to f)\) of \(f\). Eq − →−−e x ⇉gf y \operatorname {eq}\underset {\quad e \quad}. An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : However, note that the equaliser is not the only set that. Let \(\cc\) be a category, and suppose \(e: A chapter from a. Equalizer Category Theory.
From ifunny.co
Normie group kernel tensor product simplicial complex homology empty set diagram Equalizer Category Theory Learn the properties, constructions, and applications of equalizers in. An equalizer is a limit. Let \(\cc\) be a category, and suppose \(e: However, note that the equaliser is not the only set that. Equalizers are the category analogue of sets with equal. First, the equalizer satis es the property that it is a subset of xand for all x2eq(f;g), f(x). Equalizer Category Theory.
From www.youtube.com
Audio Theory Equalizer YouTube Equalizer Category Theory Let \(\cc\) be a category, and suppose \(e: Learn how to define and use equalizers and pullbacks in category theory, with intuitive explanations and diagrams. However, note that the equaliser is not the only set that. We define the equalizer of \(f\) and \(g\) to be limit \((\lim f, e: An equalizer is a limit. Equalizers are the category analogue. Equalizer Category Theory.
From www.theseasonedpodcaster.com
Best Equalizer Settings for Podcasts Our Guide to Voice EQ TSP Equalizer Category Theory An equaliser of two morphisms $f,g$ between the objects $x, y$ of a category $\mathfrak{k}$ is a morphism $e : An equalizer is a map that makes two other maps equal in a category. Let \(\cc\) be a category, and suppose \(e: Learn the properties, constructions, and applications of equalizers in. Learn how to define and use equalizers and pullbacks. Equalizer Category Theory.