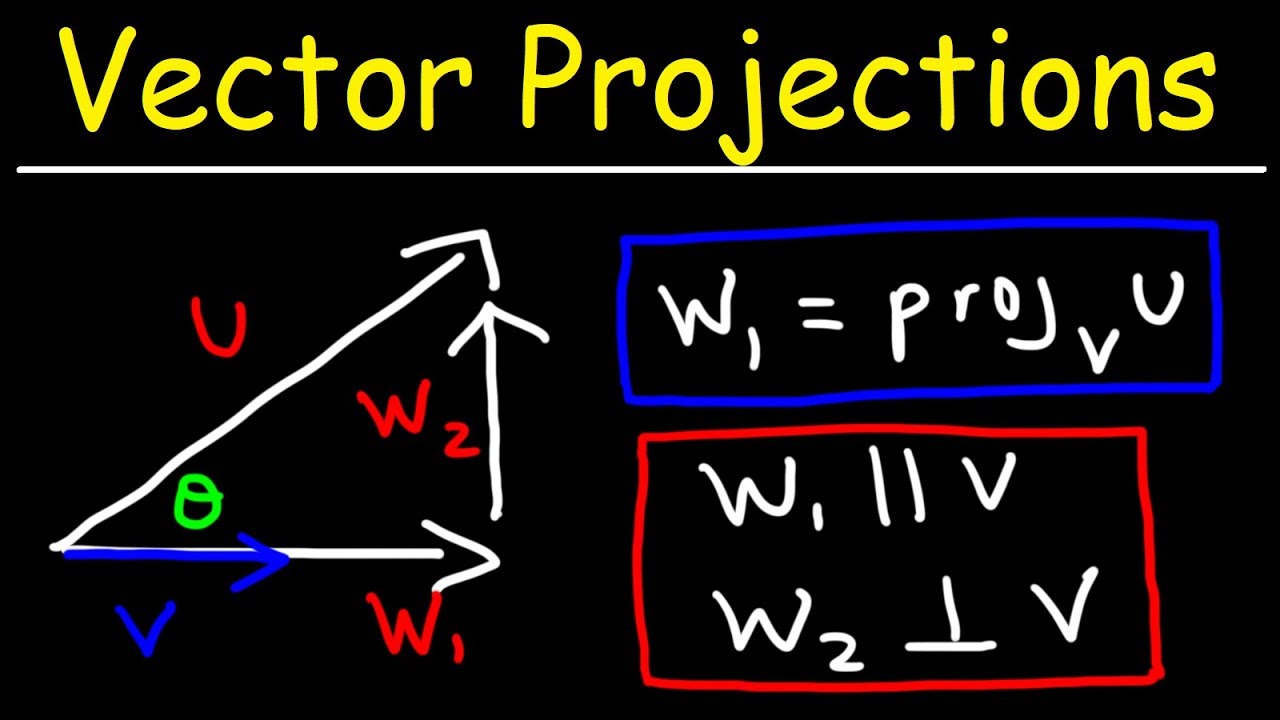
Orthogonal Projection Dot Product . Why use the dot product? Two vectors are orthogonal if the angle between them is 90 degrees. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Understand the relationship between the dot product and orthogonality. If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. Understand the relationship between the dot product and orthogonality. It is often called the inner product (or rarely the projection product) of. Vocabulary words:dot product, length, distance,. Dot product, length, distance, unit vector, unit vector. In this section, we define a product of vectors. Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. An important use of the dot product is to test whether or not two vectors are orthogonal. In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used.
from www.youtube.com
Dot product, length, distance, unit vector, unit vector. Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. Vocabulary words:dot product, length, distance,. An important use of the dot product is to test whether or not two vectors are orthogonal. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Understand the relationship between the dot product and orthogonality. Understand the relationship between the dot product and orthogonality. In this section, we define a product of vectors. In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used.
Calculus 3 Vector Projections & Orthogonal Components YouTube
Orthogonal Projection Dot Product It is often called the inner product (or rarely the projection product) of. Dot product, length, distance, unit vector, unit vector. Why use the dot product? In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. Two vectors are orthogonal if the angle between them is 90 degrees. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. It is often called the inner product (or rarely the projection product) of. Understand the relationship between the dot product and orthogonality. Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. An important use of the dot product is to test whether or not two vectors are orthogonal. Vocabulary words:dot product, length, distance,. In this section, we define a product of vectors. Understand the relationship between the dot product and orthogonality.
From www.vrogue.co
View 25 View Orthogonal Vectors Dot Product Gif Png vrogue.co Orthogonal Projection Dot Product Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. Why use the dot product? Dot product, length, distance, unit vector, unit vector. Vocabulary words:dot product, length, distance,. Two vectors are orthogonal if the angle between them is 90 degrees. In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used.. Orthogonal Projection Dot Product.
From www.studypool.com
SOLUTION Dot product properties and orthogonal projection Studypool Orthogonal Projection Dot Product Understand the relationship between the dot product and orthogonality. Understand the relationship between the dot product and orthogonality. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. In this section, we define a product of vectors. Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. In euclidean. Orthogonal Projection Dot Product.
From www.slideshare.net
Lesson 2 Vectors and the Dot Product Orthogonal Projection Dot Product Understand the relationship between the dot product and orthogonality. Two vectors are orthogonal if the angle between them is 90 degrees. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Understand the relationship between the dot product and orthogonality. Dot product, length, distance, unit vector, unit vector. It is often called the inner product (or. Orthogonal Projection Dot Product.
From www.studypool.com
SOLUTION Dot product properties and orthogonal projection Studypool Orthogonal Projection Dot Product Vocabulary words:dot product, length, distance,. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. It is often called the inner product (or rarely the projection product) of. Understand the relationship between the dot product and orthogonality. Why use the dot product? In euclidean geometry, the dot product of the cartesian coordinates of two vectors is. Orthogonal Projection Dot Product.
From www.showme.com
Dot Product and Orthogonal Vectors in 3D Math, Precalculus, Vectors Orthogonal Projection Dot Product Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. Two vectors are orthogonal if the angle between them is 90 degrees. If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. It is often called the inner product (or rarely the projection product) of. In. Orthogonal Projection Dot Product.
From ar.inspiredpencil.com
Orthogonal Vectors Dot Product Orthogonal Projection Dot Product Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Dot product, length, distance, unit vector, unit vector. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used. Vocabulary words:dot product, length, distance,.. Orthogonal Projection Dot Product.
From www.youtube.com
Dot Product, Orthogonality, and Components YouTube Orthogonal Projection Dot Product Understand the relationship between the dot product and orthogonality. Why use the dot product? It is often called the inner product (or rarely the projection product) of. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. An important use of the dot product is to test whether or not two vectors are. Orthogonal Projection Dot Product.
From www.youtube.com
Calculus 3 Vector Projections & Orthogonal Components YouTube Orthogonal Projection Dot Product If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. Two vectors are orthogonal if the angle between them is 90 degrees. It is often called the inner product (or rarely the projection product) of. Vocabulary words:dot product, length, distance,. In euclidean geometry, the dot product of the cartesian coordinates. Orthogonal Projection Dot Product.
From www.youtube.com
The Dot Product Vector and Scalar Projections YouTube Orthogonal Projection Dot Product Understand the relationship between the dot product and orthogonality. Why use the dot product? In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. Vocabulary words:dot product, length, distance,. In this section, we define a product of vectors. Understand the relationship between the dot product and orthogonality. In euclidean geometry, the dot product. Orthogonal Projection Dot Product.
From firmfunda.com
Vector Algebra Vector Dot Product First Principles Orthogonal Projection Dot Product Two vectors are orthogonal if the angle between them is 90 degrees. An important use of the dot product is to test whether or not two vectors are orthogonal. If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. In euclidean geometry, the dot product of the cartesian coordinates of. Orthogonal Projection Dot Product.
From www.youtube.com
Calculus III The Dot Product (Level 8 of 12) Scalar, Vector and Orthogonal Projection Dot Product It is often called the inner product (or rarely the projection product) of. Why use the dot product? Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Dot product, length, distance, unit vector, unit vector. In this section, we define a product of vectors. Vocabulary words:dot product, length, distance,. If the angle between ~a and. Orthogonal Projection Dot Product.
From www.youtube.com
Dot Product and Orthogonal Vectors YouTube Orthogonal Projection Dot Product If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. An important use of the dot product is to test whether or not two vectors are orthogonal. Understand the relationship between the dot product and orthogonality.. Orthogonal Projection Dot Product.
From www.studypool.com
SOLUTION Dot product properties and orthogonal projection Studypool Orthogonal Projection Dot Product In this section, we define a product of vectors. Dot product, length, distance, unit vector, unit vector. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. An important use of the dot product is to test whether or not two vectors are orthogonal. Understand the relationship between the dot product and orthogonality. Vocabulary words:dot product,. Orthogonal Projection Dot Product.
From www.tivadardanka.com
How the dot product measures similarity Mathematics of machine learning Orthogonal Projection Dot Product In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. In this section, we define a product of vectors. An important use of the dot product is to test whether or not two vectors are orthogonal. Why use the dot product? Learn the basic properties of orthogonal projections as linear transformations and as. Orthogonal Projection Dot Product.
From www.tivadardanka.com
How the dot product measures similarity Mathematics of machine learning Orthogonal Projection Dot Product An important use of the dot product is to test whether or not two vectors are orthogonal. Vocabulary words:dot product, length, distance,. Why use the dot product? It is often called the inner product (or rarely the projection product) of. If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as.. Orthogonal Projection Dot Product.
From www.onlinemathlearning.com
The Dot Product (solutions, examples, videos) Orthogonal Projection Dot Product Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Vocabulary words:dot product, length, distance,. In this section, we define a product of vectors. An important use of the dot product is to test whether or not two vectors are orthogonal. It is often called the inner product (or rarely the projection product) of. Dot product,. Orthogonal Projection Dot Product.
From www.youtube.com
Visualizing the Dot Product Angle Between Two Vectors YouTube Orthogonal Projection Dot Product Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used. Understand the relationship between the dot product and orthogonality. An important use of the dot product is to test whether or not two vectors are orthogonal. It is often called. Orthogonal Projection Dot Product.
From www.tivadardanka.com
How the dot product measures similarity Mathematics of machine learning Orthogonal Projection Dot Product Dot product, length, distance, unit vector, unit vector. Understand the relationship between the dot product and orthogonality. Understand the relationship between the dot product and orthogonality. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used. An important use of. Orthogonal Projection Dot Product.
From www.youtube.com
Engineering Mechanics Statics Theory Orthogonal Projections YouTube Orthogonal Projection Dot Product Two vectors are orthogonal if the angle between them is 90 degrees. Understand the relationship between the dot product and orthogonality. It is often called the inner product (or rarely the projection product) of. If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. Dot product suppose \(\vec{v}\) and \(\vec{w}\). Orthogonal Projection Dot Product.
From www.slideserve.com
PPT Section 3.3 PowerPoint Presentation, free download ID4282070 Orthogonal Projection Dot Product Two vectors are orthogonal if the angle between them is 90 degrees. Understand the relationship between the dot product and orthogonality. Why use the dot product? Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. Vocabulary words:dot product, length, distance,. It is often called the inner product (or rarely the projection product) of. In section. Orthogonal Projection Dot Product.
From seanballais.com
Why is the Dot Product of Two Perpendicular Vectors Zero? Sean Ballais Orthogonal Projection Dot Product In this section, we define a product of vectors. Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. An important use of the dot product is to test whether or not two vectors are orthogonal.. Orthogonal Projection Dot Product.
From www.youtube.com
Vector Projection and Dot Products YouTube Orthogonal Projection Dot Product An important use of the dot product is to test whether or not two vectors are orthogonal. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. Understand the relationship between the dot product and orthogonality. It is often called the inner product (or rarely the projection product) of. Dot product, length, distance,. Orthogonal Projection Dot Product.
From ar.inspiredpencil.com
Orthogonal Vectors Dot Product Orthogonal Projection Dot Product Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. It is often called the inner product (or rarely the projection product) of. Vocabulary words:dot product, length, distance,. Understand the relationship between the dot product and orthogonality. In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used. In this section,. Orthogonal Projection Dot Product.
From ar.inspiredpencil.com
Orthogonal Vectors Dot Product Orthogonal Projection Dot Product Dot product, length, distance, unit vector, unit vector. It is often called the inner product (or rarely the projection product) of. An important use of the dot product is to test whether or not two vectors are orthogonal. Why use the dot product? In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars.. Orthogonal Projection Dot Product.
From www.slideserve.com
PPT The Dot Product Angles Between Vectors Orthogonal Vectors Orthogonal Projection Dot Product An important use of the dot product is to test whether or not two vectors are orthogonal. Understand the relationship between the dot product and orthogonality. Understand the relationship between the dot product and orthogonality. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. It is often called the inner product (or. Orthogonal Projection Dot Product.
From ar.inspiredpencil.com
Orthogonal Projection Matrix Orthogonal Projection Dot Product Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. Two vectors are orthogonal if the angle between them is 90 degrees. Understand the relationship between the dot product and orthogonality. In euclidean geometry, the dot product of the. Orthogonal Projection Dot Product.
From www.studypool.com
SOLUTION Dot product properties and orthogonal projection Studypool Orthogonal Projection Dot Product Understand the relationship between the dot product and orthogonality. Understand the relationship between the dot product and orthogonality. Dot product, length, distance, unit vector, unit vector. An important use of the dot product is to test whether or not two vectors are orthogonal. Vocabulary words:dot product, length, distance,. In euclidean geometry, the dot product of the cartesian coordinates of two. Orthogonal Projection Dot Product.
From www.slideserve.com
PPT Dot Product PowerPoint Presentation, free download ID5554622 Orthogonal Projection Dot Product Vocabulary words:dot product, length, distance,. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. In this section, we define a product of vectors. Understand the relationship between the dot product and orthogonality. Dot product, length, distance, unit vector, unit vector. It is often called the inner product (or rarely the projection product) of. An important. Orthogonal Projection Dot Product.
From www.youtube.com
Scalar Dot Product As Vector Projection Component YouTube Orthogonal Projection Dot Product Dot product, length, distance, unit vector, unit vector. An important use of the dot product is to test whether or not two vectors are orthogonal. In this section, we define a product of vectors. Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. Understand the relationship between the dot product and orthogonality. In section 9.1,. Orthogonal Projection Dot Product.
From www.youtube.com
12.3 The dot product is zero iff two vectors are orthogonal YouTube Orthogonal Projection Dot Product If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. Dot product, length, distance, unit vector, unit vector. Understand the relationship between the dot product and orthogonality. In this section, we define a product of vectors. Understand the relationship between the dot product and orthogonality. Two vectors are orthogonal if. Orthogonal Projection Dot Product.
From ar.inspiredpencil.com
Orthogonal Vectors Dot Product Orthogonal Projection Dot Product If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. Understand the relationship between the dot product and orthogonality. Vocabulary words:dot product, length, distance,. Dot product, length, distance, unit vector, unit vector. Dot product suppose \(\vec{v}\) and \(\vec{w}\) are vectors whose component forms are \(\vec{v} =. Two vectors are orthogonal. Orthogonal Projection Dot Product.
From www.slideserve.com
PPT The Dot Product PowerPoint Presentation, free download ID5160228 Orthogonal Projection Dot Product Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Understand the relationship between the dot product and orthogonality. Two vectors are orthogonal if the angle between them is 90 degrees. Understand the relationship between the dot product and orthogonality. In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used.. Orthogonal Projection Dot Product.
From caknowledge.com
Know More About Dot Products! Projection of a Vector Orthogonal Projection Dot Product An important use of the dot product is to test whether or not two vectors are orthogonal. In this section, we define a product of vectors. Dot product, length, distance, unit vector, unit vector. It is often called the inner product (or rarely the projection product) of. Two vectors are orthogonal if the angle between them is 90 degrees. In. Orthogonal Projection Dot Product.
From rehangetwin.blogspot.com
Learn maths in an easy way definition of the dot product Orthogonal Projection Dot Product Vocabulary words:dot product, length, distance,. Why use the dot product? In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used. In this section, we define a product of vectors. In section 9.1, we learned how add and subtract vectors and how to multiply vectors by scalars. Learn the basic properties of orthogonal projections as. Orthogonal Projection Dot Product.
From www.youtube.com
The Dot Product is Equal to Zero for Perpendicular Vectors YouTube Orthogonal Projection Dot Product Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Vocabulary words:dot product, length, distance,. In euclidean geometry, the dot product of the cartesian coordinates of two vectors is widely used. If the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as. In this section, we define. Orthogonal Projection Dot Product.