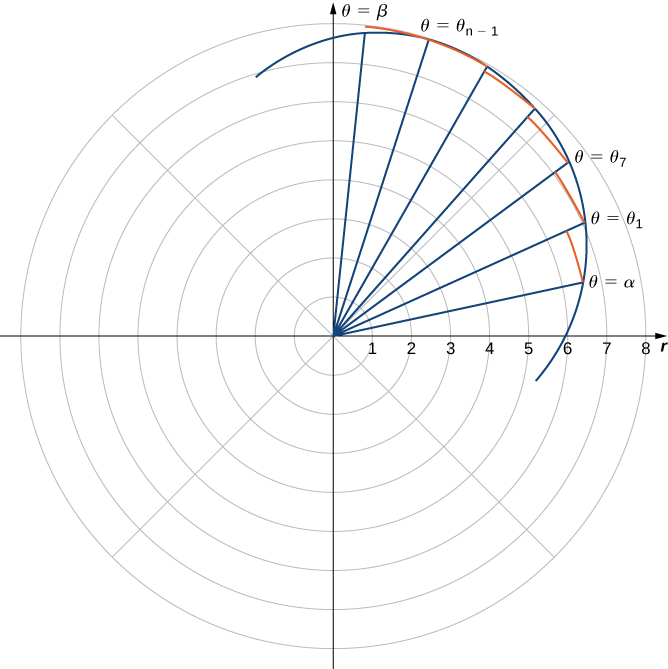
X Hat In Polar Coordinates . Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. However, in polar coordinates, we have the. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar.
from philschatz.com
Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. However, in polar coordinates, we have the. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,.
Area and Arc Length in Polar Coordinates · Calculus
X Hat In Polar Coordinates To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. However, in polar coordinates, we have the. Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\).
From www.physicsbootcamp.org
Motion in Polar Coordinates X Hat In Polar Coordinates However, in polar coordinates, we have the. Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). In this way, a point. X Hat In Polar Coordinates.
From www.cuemath.com
Polar Coordinates Cuemath X Hat In Polar Coordinates To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are. X Hat In Polar Coordinates.
From www.physicsbootcamp.org
Motion in Polar Coordinates X Hat In Polar Coordinates Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). To find the area between two curves in the polar coordinate system,. X Hat In Polar Coordinates.
From pressbooks.nscc.ca
Conic Sections in Polar Coordinates Algebra and Trigonometry OpenStax X Hat In Polar Coordinates In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. In this way, a point p that has coordinates (x, y) in the rectangular system can be. X Hat In Polar Coordinates.
From www.dummies.com
How to Graph Polar Coordinates with Negative Values dummies X Hat In Polar Coordinates In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. However, in polar coordinates, we have the. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. The area of a region in polar. X Hat In Polar Coordinates.
From calcworkshop.com
Converting Polar to Rectangular Coordinates (19+ Examples!) X Hat In Polar Coordinates In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). To find the area between two curves in the polar coordinate system, first find the points of intersection, then. X Hat In Polar Coordinates.
From socratic.org
Polar Coordinates Trigonometry Socratic X Hat In Polar Coordinates The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. To find the area between two curves in the polar coordinate system,. X Hat In Polar Coordinates.
From www.targetmathematics.org
Polar Coordinate System Part (1) X Hat In Polar Coordinates To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by. X Hat In Polar Coordinates.
From quizlet.com
In given exercise, plot the point given in polar coordinates Quizlet X Hat In Polar Coordinates The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by. X Hat In Polar Coordinates.
From www.slideserve.com
PPT Polar Coordinates PowerPoint Presentation, free download ID6528559 X Hat In Polar Coordinates Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In this way, a point p that has coordinates (x, y). X Hat In Polar Coordinates.
From www.physicsbootcamp.org
Motion in Polar Coordinates X Hat In Polar Coordinates However, in polar coordinates, we have the. In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. In cartesian to polar transformations,. X Hat In Polar Coordinates.
From quizlet.com
Plot the following points (given in polar coordinates). Then Quizlet X Hat In Polar Coordinates The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. However, in polar coordinates, we have the. In cartesian coordinates we have the coordinates x,y,z, and. X Hat In Polar Coordinates.
From www.cuemath.com
Polar Coordinates Cuemath X Hat In Polar Coordinates To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. The area of a region in polar coordinates defined by the equation \(r=f(θ)\). X Hat In Polar Coordinates.
From www.slideserve.com
PPT Polar Coordinates z= rcis Ө PowerPoint Presentation, free X Hat In Polar Coordinates To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by. X Hat In Polar Coordinates.
From www.researchgate.net
State trajectories of x(t) in polar coordinates (hU=3.5201, hL=0.1 X Hat In Polar Coordinates In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. In cartesian to polar transformations, the unit vectors $\hat x$,. X Hat In Polar Coordinates.
From en.neurochispas.com
Polar Coordinates Formulas and Diagrams Neurochispas X Hat In Polar Coordinates In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx. X Hat In Polar Coordinates.
From www.chegg.com
Solved 3. Each of the following points is given in polar X Hat In Polar Coordinates In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. However, in polar coordinates, we have the. In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. In cartesian coordinates we have the coordinates x,y,z, and the position vector. X Hat In Polar Coordinates.
From www.slideserve.com
PPT Polar Coordinates PowerPoint Presentation, free download ID6155368 X Hat In Polar Coordinates Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. However, in polar coordinates, we have the. The area of a region in polar coordinates. X Hat In Polar Coordinates.
From www.ck12.org
Polar Coordinates CK12 Foundation X Hat In Polar Coordinates Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). However, in polar coordinates, we have the. To find the area between. X Hat In Polar Coordinates.
From math.stackexchange.com
derivatives How to differentiate a function defined in polar X Hat In Polar Coordinates In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. To find the area between two curves in the polar coordinate system, first find the points of intersection, then. X Hat In Polar Coordinates.
From www.khanacademy.org
Polar coordinates Angular Movement Khan Academy X Hat In Polar Coordinates However, in polar coordinates, we have the. Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. The area of a. X Hat In Polar Coordinates.
From philschatz.com
Area and Arc Length in Polar Coordinates · Calculus X Hat In Polar Coordinates The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to. X Hat In Polar Coordinates.
From math.gallery.video
What are Polar Coordinates in Math? How do they Work? Math Tutor X Hat In Polar Coordinates However, in polar coordinates, we have the. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. To find the area between two curves in the. X Hat In Polar Coordinates.
From learninglibcogar.z4.web.core.windows.net
How To Determine Polar Coordinates X Hat In Polar Coordinates In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. However, in polar coordinates, we have the. In cartesian coordinates we have the coordinates x,y,z,. X Hat In Polar Coordinates.
From www.slideserve.com
PPT Polar Coordinates Polar and Rectangular Coordinates PowerPoint X Hat In Polar Coordinates In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. However, in polar coordinates, we have the. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). Are you saying that, in a rotation problem, the. X Hat In Polar Coordinates.
From rumble.com
Conics in Polar Coordinates Example 2 Ellipse X Hat In Polar Coordinates The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. However, in polar coordinates, we have the. In cartesian coordinates we have the coordinates x,y,z,. X Hat In Polar Coordinates.
From www.slideserve.com
PPT Chapter 11 Polar Coordinates and Complex Numbers PowerPoint X Hat In Polar Coordinates To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. In this way, a point p that has coordinates (x, y) in the. X Hat In Polar Coordinates.
From people.tamu.edu
Vectors, an elementary tutorial X Hat In Polar Coordinates In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. However, in polar coordinates, we have the. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). To find the area between two curves. X Hat In Polar Coordinates.
From en.neurochispas.com
Rectangular to Polar Coordinates Formulas and Examples Neurochispas X Hat In Polar Coordinates The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r. X Hat In Polar Coordinates.
From www.youtube.com
lec2 double integral in polar coordinates YouTube X Hat In Polar Coordinates Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat. X Hat In Polar Coordinates.
From www.youtube.com
graphing a point in polar coordinates YouTube X Hat In Polar Coordinates Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. The area of a region in polar coordinates defined by the equation. X Hat In Polar Coordinates.
From quizlet.com
Plot the point in polar coordinates and find the correspondi Quizlet X Hat In Polar Coordinates The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(a=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\). However, in polar coordinates, we have the. To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian coordinates we have the coordinates x,y,z,. X Hat In Polar Coordinates.
From www.bartleby.com
Sets in polar coordinates Sketch the following sets of points. 20 X Hat In Polar Coordinates To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas. In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. However, in polar coordinates, we have the. Are you saying that, in a rotation problem, the relevant polar. X Hat In Polar Coordinates.
From mungfali.com
Polar Coordinates Conversion X Hat In Polar Coordinates In cartesian to polar transformations, the unit vectors $\hat x$, $\hat y$ are transformed to $\hat r$, $\hat \theta$,. Are you saying that, in a rotation problem, the relevant polar coordinate at each tick of the clock is essentially just a generator of the appropriate. The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\). X Hat In Polar Coordinates.
From mathhints.com
Polar Coordinates, Equations, and Graphs Math Hints X Hat In Polar Coordinates However, in polar coordinates, we have the. In this way, a point p that has coordinates (x, y) in the rectangular system can be described equivalently in the polar. In cartesian coordinates we have the coordinates x,y,z, and the position vector is described by r (x,y,z) = xˆx + + yˆy + zˆz. To find the area between two curves. X Hat In Polar Coordinates.