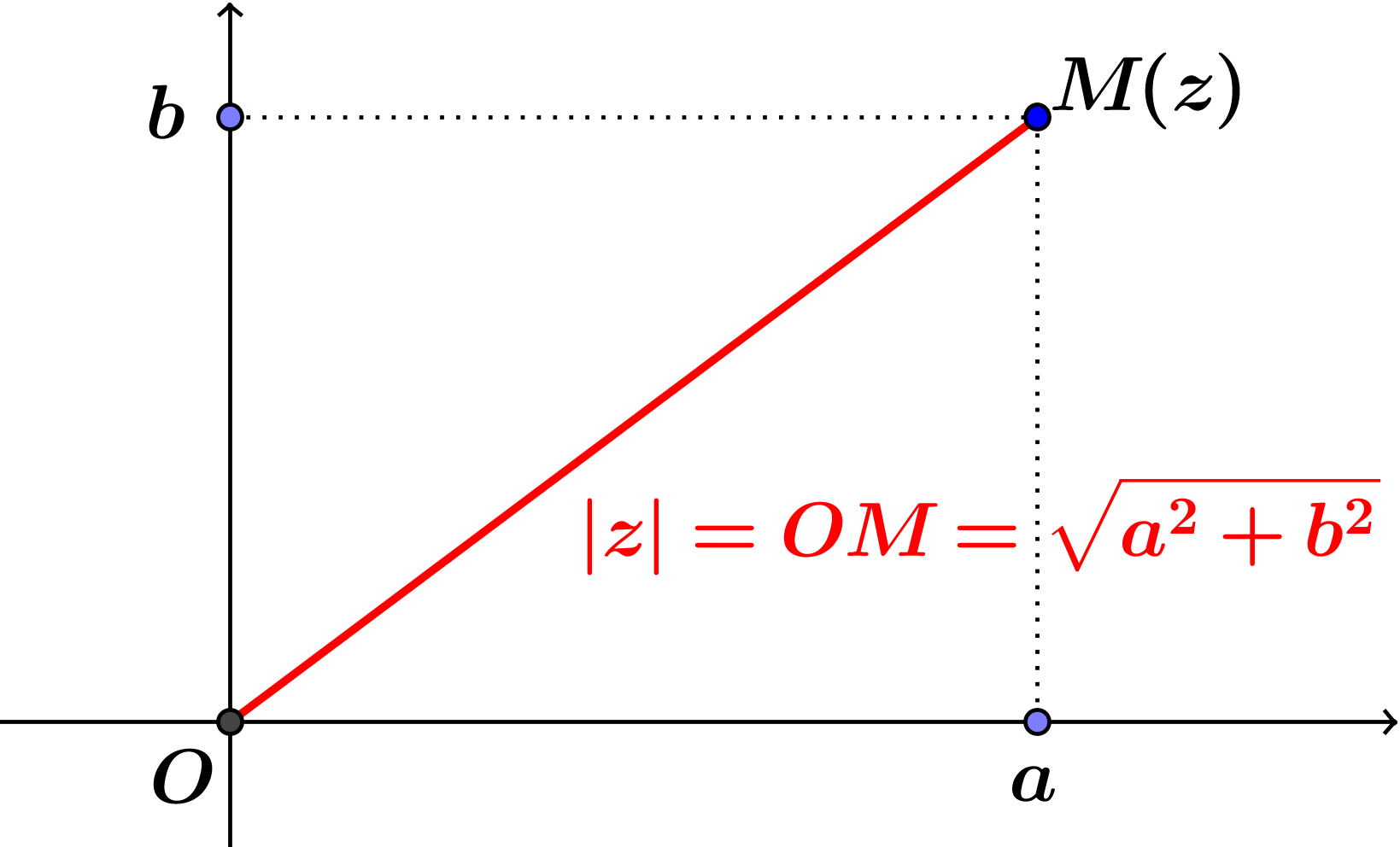
Module De Z-I . |z| = \sqrt {a^2+b^2} ∣z∣ = a2. An abelian group gis divisible i gis isomorphic. On rappelle que le module est synonyme de distance. In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. Propriétés sur le module : The most basic ring is undoutedly the ring z of all integers. Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. Sa formule pour les nombres complexes z et z' est : On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : Cette valeur est issu d'un triangle.
from pdfprof.com
The most basic ring is undoutedly the ring z of all integers. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : Cette valeur est issu d'un triangle. An abelian group gis divisible i gis isomorphic. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. Propriétés sur le module : On rappelle que le module est synonyme de distance. Sa formule pour les nombres complexes z et z' est :
soit f la transformation qui a tout nombre complexe z non nul associe
Module De Z-I An abelian group gis divisible i gis isomorphic. The most basic ring is undoutedly the ring z of all integers. In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. An abelian group gis divisible i gis isomorphic. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. On rappelle que le module est synonyme de distance. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. Propriétés sur le module : Cette valeur est issu d'un triangle. Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. Sa formule pour les nombres complexes z et z' est : On définit le module de z, noté |z| ∣z∣ comme la quantité suivante :
From www.strandhotel-duenenmeer.de
SPABistro Strandhotel Dünenmeer Module De Z-I Propriétés sur le module : On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. On rappelle que le module est synonyme de distance. Cette valeur est issu d'un triangle. In mathematics,. Module De Z-I.
From studylibfr.com
Module et conjugué d`un nombre complexe 1 z Forme Module De Z-I Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. On rappelle que le module est synonyme de distance. Propriétés sur le module : In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. Sa formule pour les nombres complexes. Module De Z-I.
From wiringdbbawdex.z4.web.core.windows.net
What Is The Use Of Esp8266 Wifi Module Module De Z-I Propriétés sur le module : On rappelle que le module est synonyme de distance. An abelian group gis divisible i gis isomorphic. Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. Cette valeur est issu d'un triangle. The most basic ring is undoutedly the ring z of all integers. Sa formule pour. Module De Z-I.
From www.youtube.com
Lien avec la physique module et argument de z =1/(jLCw) YouTube Module De Z-I Sa formule pour les nombres complexes z et z' est : Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. Cette valeur est issu d'un triangle. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : An abelian group gis divisible i gis isomorphic. |z| = \sqrt {a^2+b^2}. Module De Z-I.
From exoohoqvs.blob.core.windows.net
Module De Z^2 at Lawrence Bender blog Module De Z-I Cette valeur est issu d'un triangle. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. The most basic ring is undoutedly the ring z of all integers. Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. Sa formule pour les nombres complexes z et z' est : In the case of a finite abelian. Module De Z-I.
From exoohoqvs.blob.core.windows.net
Module De Z^2 at Lawrence Bender blog Module De Z-I In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. The most basic ring is undoutedly the ring z of all integers. On rappelle que le module est synonyme de distance. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. Sa formule pour les nombres complexes z et z'. Module De Z-I.
From wiringfixsqueellveted1.z13.web.core.windows.net
Gm Hei Ignition Module 5 Pin Module De Z-I |z| = \sqrt {a^2+b^2} ∣z∣ = a2. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : Propriétés sur le module : Cette valeur est issu d'un triangle. On rappelle que le module. Module De Z-I.
From www.ebay.co.uk
Convient pour module de contrôle de ballast phare Classe S W222 X222 Module De Z-I On rappelle que le module est synonyme de distance. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. Propriétés sur le module : Soit z = a+ib, a,b \in \mathbb {r} z. Module De Z-I.
From maths-space.com
Exercices Résolution d'équations complexes de premier degré maths Module De Z-I The most basic ring is undoutedly the ring z of all integers. On rappelle que le module est synonyme de distance. An abelian group gis divisible i gis isomorphic. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. Cette valeur est issu d'un triangle. Propriétés sur. Module De Z-I.
From www.a4.fr
AutoProg Module DEL monté [KAPMDELM] Module De Z-I In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. Propriétés sur le module : On rappelle que le module est synonyme de distance. The most basic ring is undoutedly the ring z of all integers. Soit z = a+ib, a,b \in \mathbb {r} z = a+. Module De Z-I.
From www.alibaba.com
Cheap Z Axis Cnc Module 5 Axis Linear Slide Guide For Xyz Linear Stage Module De Z-I On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : On rappelle que le module est synonyme de distance. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. In mathematics, especially in the area of. Module De Z-I.
From www.civilmania.com
Module de réaction horizontal de sol Sols & fondations CIVILMANIA Module De Z-I In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q. Module De Z-I.
From www.aliexpress.com
Buy Smart Electronics 5V 1 One Channel Relay Module Module De Z-I On rappelle que le module est synonyme de distance. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. The most basic ring is undoutedly the ring z of all integers. In the. Module De Z-I.
From www.nagwa.com
Vidéo question Trouver le module des nombres complexes Nagwa Module De Z-I In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. An abelian group gis divisible i gis isomorphic. On rappelle que le module est synonyme de distance. Propriétés sur le module : In the case of a finite abelian group, the isomorphism classes determined by the prime. Module De Z-I.
From www.simbiosishost.com
nettoyeur Posséder restaurant calcul tassement sol Dépouiller cowboy Module De Z-I In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante :. Module De Z-I.
From www.slideserve.com
PPT Genèse des nombres complexes PowerPoint Presentation, free Module De Z-I Propriétés sur le module : An abelian group gis divisible i gis isomorphic. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. Sa formule pour les nombres complexes z et z' est. Module De Z-I.
From www.universetoday.com
Reconfigurable Archives Universe Today Module De Z-I On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : The most basic ring is undoutedly the ring z of all integers. Sa formule pour les nombres complexes z et z' est : On rappelle que le module est synonyme de distance. Cette valeur est issu d'un triangle. An abelian group gis divisible i gis isomorphic.. Module De Z-I.
From exoohoqvs.blob.core.windows.net
Module De Z^2 at Lawrence Bender blog Module De Z-I Propriétés sur le module : Sa formule pour les nombres complexes z et z' est : In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. On définit le module. Module De Z-I.
From www.youtube.com
partie 8 ( Module de z ) complexes 2022 YouTube Module De Z-I The most basic ring is undoutedly the ring z of all integers. Cette valeur est issu d'un triangle. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. Sa formule pour les nombres complexes z et z' est :. Module De Z-I.
From www.nagwa.com
Vidéo question Calcul de la puissance d’un nombre complexe sous Module De Z-I In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. An abelian group gis divisible i gis isomorphic. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un. Module De Z-I.
From nshopvn.com
Module 1 Relay Kích Mức Thấp 5VDC Module De Z-I Sa formule pour les nombres complexes z et z' est : On rappelle que le module est synonyme de distance. The most basic ring is undoutedly the ring z of all integers. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : An abelian group gis divisible i gis. Module De Z-I.
From wiringmonoplane.z21.web.core.windows.net
Relay Module 8 Channel 5v Module De Z-I On rappelle que le module est synonyme de distance. Sa formule pour les nombres complexes z et z' est : Propriétés sur le module : Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : The most basic ring. Module De Z-I.
From z-uno.z-wave.me
Module Module De Z-I On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. Sa formule pour les nombres complexes z et z' est : An abelian group gis divisible i gis isomorphic. In the case of a finite abelian group, the isomorphism. Module De Z-I.
From www.pinterest.com
Complex Analysis Proof z + conjugate(z) = 2*Re(z) Complex analysis Module De Z-I On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : Propriétés sur le module : Sa formule pour les nombres complexes z et z' est : Cette valeur est issu d'un triangle. Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. |z| = \sqrt {a^2+b^2} ∣z∣ = a2.. Module De Z-I.
From www.rockwellautomation.com
Compact 5000 I/O Modules AllenBradley Module De Z-I Propriétés sur le module : On rappelle que le module est synonyme de distance. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain.. Module De Z-I.
From www.iiab.me
Using single 5V relay module (jqc3ffsz) Asking for help Module De Z-I On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : An abelian group gis divisible i gis isomorphic. Sa formule pour les nombres complexes z et z' est : |z| = \sqrt {a^2+b^2} ∣z∣ = a2. Cette valeur est issu d'un triangle. The most basic ring is undoutedly the ring z of all integers. On rappelle. Module De Z-I.
From hxekhdgga.blob.core.windows.net
Module De Z Nombre Complexe at Stacey Malin blog Module De Z-I Propriétés sur le module : In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. On rappelle que le module est synonyme de distance. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all.. Module De Z-I.
From www.youtube.com
Element de Mécanique S1 Vecteur et son Module Chap 1 YouTube Module De Z-I On rappelle que le module est synonyme de distance. Propriétés sur le module : In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. Cette valeur est issu d'un triangle. The most basic ring is undoutedly the ring z of. Module De Z-I.
From pdfprof.com
soit f la transformation qui a tout nombre complexe z non nul associe Module De Z-I An abelian group gis divisible i gis isomorphic. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. Propriétés sur le module : Cette valeur est issu d'un triangle. In mathematics, especially in the area of abstract algebra known as. Module De Z-I.
From exoohoqvs.blob.core.windows.net
Module De Z^2 at Lawrence Bender blog Module De Z-I |z| = \sqrt {a^2+b^2} ∣z∣ = a2. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. On définit le module de z, noté |z| ∣z∣ comme la quantité suivante : On rappelle que le module est synonyme de distance. Sa formule pour les nombres complexes z. Module De Z-I.
From www.teachoo.com
Ex 5.2, 1 Find modulus and argument of z = 1 i root 3 Module De Z-I In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. On rappelle que le module est synonyme de distance. An abelian group gis divisible i gis isomorphic. Cette valeur est issu d'un triangle. Propriétés sur le module : Soit z = a+ib, a,b \in \mathbb {r} z. Module De Z-I.
From www.nagwa.com
Vidéo question Déterminer le module des nombres complexes sous forme Module De Z-I In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. |z| = \sqrt {a^2+b^2} ∣z∣ = a2. Soit z = a+ib, a,b \in \mathbb {r} z = a+ ib,a,b ∈ r un nombre complexe. In mathematics, especially in the area of abstract algebra known as module theory,. Module De Z-I.
From www.youtube.com
Module et argument d'un nombre complexe YouTube Module De Z-I In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module q that shares certain. An abelian group gis divisible i gis isomorphic. The most basic ring is undoutedly. Module De Z-I.
From www.youtube.com
Calculer le Module d'un Nombre Complexe Pigerlesmaths YouTube Module De Z-I Sa formule pour les nombres complexes z et z' est : On rappelle que le module est synonyme de distance. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. Propriétés sur le module : Cette valeur est issu d'un triangle. On définit le module de z,. Module De Z-I.
From www.youtube.com
Comment calculer le module z d'un nombre complexe z ? YouTube Module De Z-I The most basic ring is undoutedly the ring z of all integers. Propriétés sur le module : Cette valeur est issu d'un triangle. In the case of a finite abelian group, the isomorphism classes determined by the prime factorization of the order and then listing all. In mathematics, especially in the area of abstract algebra known as module theory, an. Module De Z-I.