Inverse Demand Function Given By . In this video, we learn about the inverse demand function, specifically how to derive the inverse. This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. This means that the market inverse demand curve (i.e. Suppose a single monopolist were. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output.
from www.slideserve.com
This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. In this video, we learn about the inverse demand function, specifically how to derive the inverse. Suppose a single monopolist were. This means that the market inverse demand curve (i.e.
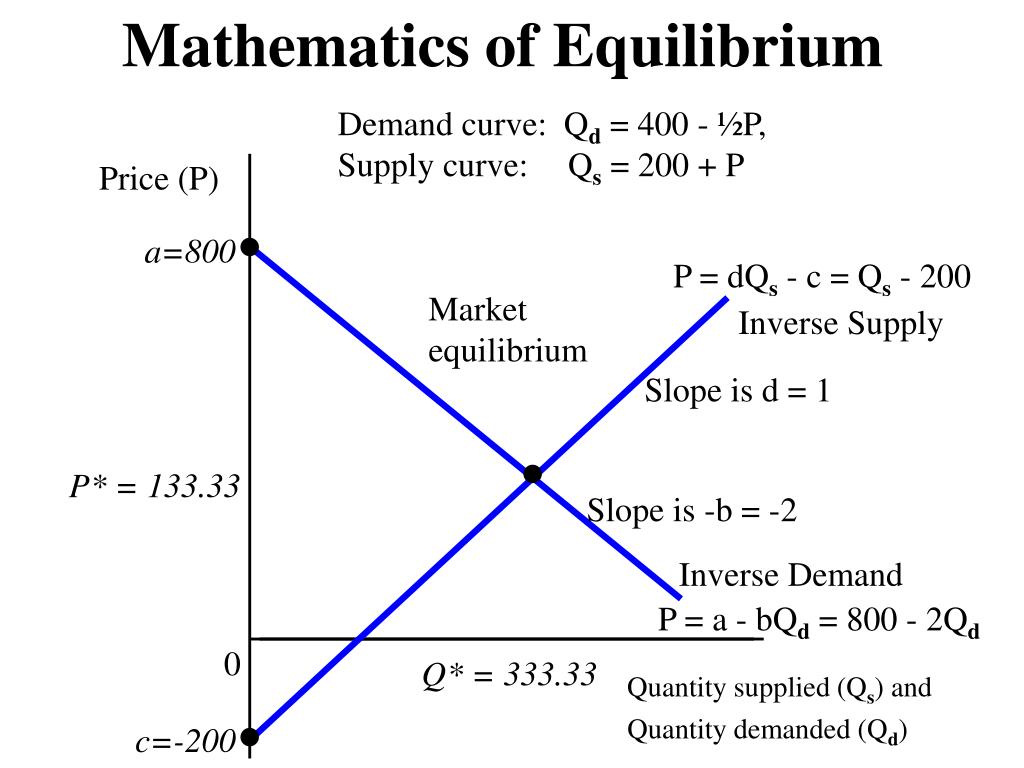
PPT Demand and Supply PowerPoint Presentation, free download ID1811415
Inverse Demand Function Given By Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. This means that the market inverse demand curve (i.e. Suppose a single monopolist were. This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. In this video, we learn about the inverse demand function, specifically how to derive the inverse.
From www.youtube.com
Inverse demand function Why are Prices on the y axis on the Demand Curve? Beyond the Inverse Demand Function Given By This means that the market inverse demand curve (i.e. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. This post shows a. Inverse Demand Function Given By.
From www.numerade.com
SOLVED Suppose the inverse demand function for two Cournot duopolists is given by P = 10 (Q1 Inverse Demand Function Given By Suppose a single monopolist were. This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total. Inverse Demand Function Given By.
From www.youtube.com
How to calculate Inverse Supply and Inverse Demand YouTube Inverse Demand Function Given By Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. Suppose a single monopolist were. In. Inverse Demand Function Given By.
From www.chegg.com
Solved Demand function 7400 0.5 Inverse demand function Inverse Demand Function Given By Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. Suppose a single. Inverse Demand Function Given By.
From penpoin.com
Inverse demand function — Penpoin. Inverse Demand Function Given By Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. This means that the market inverse demand curve (i.e. In this video, we learn about the inverse demand function, specifically how to derive the inverse. This post shows a trick for solving these best response functions. Inverse Demand Function Given By.
From www.slideserve.com
PPT Chapter 2 PowerPoint Presentation, free download ID6033847 Inverse Demand Function Given By Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. In this video, we learn about the inverse demand function, specifically how to derive the inverse. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is. Inverse Demand Function Given By.
From www.slideserve.com
PPT Course outline I PowerPoint Presentation, free download ID248879 Inverse Demand Function Given By This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. In this video, we learn about the inverse demand function, specifically how to derive the inverse.. Inverse Demand Function Given By.
From www.slideserve.com
PPT Topic 1 PowerPoint Presentation, free download ID3198681 Inverse Demand Function Given By This means that the market inverse demand curve (i.e. In this video, we learn about the inverse demand function, specifically how to derive the inverse. Suppose a single monopolist were. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $. Inverse Demand Function Given By.
From www.chegg.com
Solved Given the following inverse demand function Inverse Demand Function Given By This means that the market inverse demand curve (i.e. Suppose a single monopolist were. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry. Inverse Demand Function Given By.
From www.youtube.com
Inverse Demand Function YouTube Inverse Demand Function Given By Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $. Inverse Demand Function Given By.
From www.youtube.com
Inverse Demand Vs. Demand Function Price on the yaxis? Weird. YouTube Inverse Demand Function Given By This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. This means that the market inverse demand curve (i.e. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively,. Inverse Demand Function Given By.
From www.chegg.com
Solved 5. Consider a market with inverse demand function Inverse Demand Function Given By Suppose a single monopolist were. This means that the market inverse demand curve (i.e. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. In this video, we learn about the inverse demand function, specifically how to derive the inverse. This post shows a trick for solving these best response functions without using. Inverse Demand Function Given By.
From www.numerade.com
SOLVEDA monopolist’s inverse demand function is P = 100 Q. The company produces output at two Inverse Demand Function Given By Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. Let the inverse demand function and the cost function be given by p = 50 − 2q and c. Inverse Demand Function Given By.
From www.chegg.com
Solved HW8 Suppose the inverse demand function for a Inverse Demand Function Given By In this video, we learn about the inverse demand function, specifically how to derive the inverse. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. This means that the market inverse demand curve (i.e. Use the inverse demand function. Inverse Demand Function Given By.
From www.chegg.com
Solved Inverse demand function Px = 14800 D 2 Qxa Inverse Demand Function Given By Suppose a single monopolist were. This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. In this video, we learn about the inverse demand function, specifically how to derive the inverse. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp. Inverse Demand Function Given By.
From www.chegg.com
Solved The inverse demand function and supply function for a Inverse Demand Function Given By Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. In this video, we learn about. Inverse Demand Function Given By.
From www.wallstreetmojo.com
Demand Function What Is It, Formula, Example, Types, Inverse Inverse Demand Function Given By In this video, we learn about the inverse demand function, specifically how to derive the inverse. This means that the market inverse demand curve (i.e. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. This post shows a trick. Inverse Demand Function Given By.
From www.slideserve.com
PPT Chapter 6 Demand PowerPoint Presentation, free download ID5367307 Inverse Demand Function Given By This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. Suppose a single monopolist were. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total. Inverse Demand Function Given By.
From www.chegg.com
Solved 1) Given the graph of a market's inverse supply and Inverse Demand Function Given By Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. This means that the market inverse demand curve (i.e.. Inverse Demand Function Given By.
From www.chegg.com
Solved d. Determine the demand function and inverse demand Inverse Demand Function Given By Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. This post shows a trick for solving these best response functions without using. Inverse Demand Function Given By.
From www.chegg.com
Solved HW8 Suppose the inverse demand function for a Inverse Demand Function Given By This means that the market inverse demand curve (i.e. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. Suppose a single monopolist were. In this video, we learn about the inverse demand function, specifically how to derive the inverse. This post shows a trick for solving these best response functions without using. Inverse Demand Function Given By.
From www.slideserve.com
PPT BUSINESS ECONOMICS PowerPoint Presentation, free download ID6134914 Inverse Demand Function Given By Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. This post shows a trick for. Inverse Demand Function Given By.
From www.slideserve.com
PPT Demand PowerPoint Presentation, free download ID237525 Inverse Demand Function Given By This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. This means that the market inverse demand curve (i.e. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively,. Inverse Demand Function Given By.
From www.chegg.com
Solved The inverse demand function of a group of consumers Inverse Demand Function Given By Suppose a single monopolist were. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. This means that the market inverse demand curve (i.e. In this video, we learn about the inverse demand function, specifically how to derive the inverse. This post shows a trick for solving these best response functions without using. Inverse Demand Function Given By.
From www.chegg.com
Solved The inverse demand function for a product is given by Inverse Demand Function Given By Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. This means that the market inverse demand curve (i.e. In this video, we. Inverse Demand Function Given By.
From www.slideserve.com
PPT Demand and Supply PowerPoint Presentation, free download ID1811415 Inverse Demand Function Given By Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. Suppose a single monopolist were. This means that the market inverse demand curve (i.e. This post shows a trick. Inverse Demand Function Given By.
From www.chegg.com
Solved Granh of Inverse Demand Finnction Using the inverse Inverse Demand Function Given By Suppose a single monopolist were. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. In this video, we learn about the inverse demand function, specifically. Inverse Demand Function Given By.
From www.slideserve.com
PPT Managerial Economics & Business Strategy PowerPoint Presentation ID1629817 Inverse Demand Function Given By This means that the market inverse demand curve (i.e. This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post. In this video, we learn about the inverse demand function, specifically how to derive the inverse. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $. Inverse Demand Function Given By.
From slideplayer.com
Molly W. Dahl University Econ 101 Spring ppt download Inverse Demand Function Given By In this video, we learn about the inverse demand function, specifically how to derive the inverse. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. This means that the market inverse demand curve (i.e. Suppose a single monopolist were. Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $. Inverse Demand Function Given By.
From www.chegg.com
Solved 1. Derive the inverse demand function and the demand Inverse Demand Function Given By Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. In this video, we learn about the inverse demand function, specifically how to derive the inverse. This post shows a trick for solving these best response functions without using calculus, although a calculus based method is shown at the end of the post.. Inverse Demand Function Given By.
From www.chegg.com
Solved Suppose the (inverse) demand function for a Inverse Demand Function Given By Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. In this video, we learn about the inverse demand function, specifically how to derive the inverse. Suppose a single monopolist were. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative. Inverse Demand Function Given By.
From www.researchgate.net
Premerger and postmerger residual inverse demand functions faced by the... Download Scientific Inverse Demand Function Given By Given $$ e=\frac{dq}{dp}*\frac{p}{q}, $$ where $ e $ is elasticity, $ dq/dp $ is first derivative of. This means that the market inverse demand curve (i.e. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. In this video, we learn about the inverse demand function,. Inverse Demand Function Given By.
From www.chegg.com
Solved 1. Given the inverse demand function Inverse Demand Function Given By In this video, we learn about the inverse demand function, specifically how to derive the inverse. Let the inverse demand function and the cost function be given by p = 50 − 2q and c = 10 + 2q respectively, where q is total industry output. This post shows a trick for solving these best response functions without using calculus,. Inverse Demand Function Given By.
From www.chegg.com
Solved Given the inverse demand function P=60−3/4Q the Inverse Demand Function Given By Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. In this video, we learn about the inverse demand function, specifically how to derive the inverse. Let the inverse demand function and the cost function be given by p = 50 − 2q and c =. Inverse Demand Function Given By.
From www.chegg.com
Solved Given the following inverse demand and supply Inverse Demand Function Given By This means that the market inverse demand curve (i.e. Use the inverse demand function to calculate total revenue (tr = pq) and derive marginal revenue (mr), which is the first derivative of total. In this video, we learn about the inverse demand function, specifically how to derive the inverse. This post shows a trick for solving these best response functions. Inverse Demand Function Given By.