Is Matrix A An Orthogonal Matrix . a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. In particular, taking v = w means that lengths. a matrix a ∈ gl. Also, the product of an orthogonal matrix and its transpose is equal to i. For a matrix 𝐴 to be orthogonal, it must be. a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. N (r) is orthogonal if av · aw = v · w for all vectors v and w. An orthogonal matrix is a square matrix. A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1.
from www.chegg.com
A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. For a matrix 𝐴 to be orthogonal, it must be. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. a matrix a ∈ gl. N (r) is orthogonal if av · aw = v · w for all vectors v and w. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. Also, the product of an orthogonal matrix and its transpose is equal to i. a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. An orthogonal matrix is a square matrix.
Solved For the matrix A, find an orthogonal matrix P such
Is Matrix A An Orthogonal Matrix Also, the product of an orthogonal matrix and its transpose is equal to i. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Also, the product of an orthogonal matrix and its transpose is equal to i. An orthogonal matrix is a square matrix. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. N (r) is orthogonal if av · aw = v · w for all vectors v and w. A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. In particular, taking v = w means that lengths. a matrix a ∈ gl. For a matrix 𝐴 to be orthogonal, it must be. a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose.
From www.youtube.com
Properties of Orthogonal Matrix Example1 YouTube Is Matrix A An Orthogonal Matrix N (r) is orthogonal if av · aw = v · w for all vectors v and w. a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix.. Is Matrix A An Orthogonal Matrix.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Is Matrix A An Orthogonal Matrix A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. An orthogonal matrix is a square matrix. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. For a matrix 𝐴 to be orthogonal, it must be. a n×n matrix. Is Matrix A An Orthogonal Matrix.
From rilohs.weebly.com
Orthogonal matrix rilohs Is Matrix A An Orthogonal Matrix N (r) is orthogonal if av · aw = v · w for all vectors v and w. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. In particular, taking v. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
ATMH Unit 7 Orthogonal Matrices 3 equivalent statements (Part 1 Is Matrix A An Orthogonal Matrix a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. Also, the product of an orthogonal matrix and its transpose is equal to i. In particular, taking v = w means that lengths. For a matrix 𝐴 to be orthogonal, it must be. An orthogonal matrix is a square matrix.. Is Matrix A An Orthogonal Matrix.
From askfilo.com
Example 8. If A is an invertible matrix and orthogonal matrix of the orde.. Is Matrix A An Orthogonal Matrix a matrix a ∈ gl. Also, the product of an orthogonal matrix and its transpose is equal to i. An orthogonal matrix is a square matrix. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. N (r) is orthogonal if av · aw = v · w for. Is Matrix A An Orthogonal Matrix.
From www.chegg.com
Solved Triangularisation with an orthogonal matrix Example Is Matrix A An Orthogonal Matrix A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For a matrix 𝐴 to be orthogonal, it must be. N (r) is orthogonal if av · aw = v · w for all vectors. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
【Orthogonality】06 Orthogonal matrix YouTube Is Matrix A An Orthogonal Matrix For a matrix 𝐴 to be orthogonal, it must be. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. a matrix a ∈ gl. An. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
Orthogonal Matrix example YouTube Is Matrix A An Orthogonal Matrix For a matrix 𝐴 to be orthogonal, it must be. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. In particular, taking v = w means that lengths. a. Is Matrix A An Orthogonal Matrix.
From gateoverflow.in
Linear Algebra Engineering Maths Orthogonal Matrix Is Matrix A An Orthogonal Matrix a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. a matrix a ∈ gl. N (r) is orthogonal if av · aw = v · w for all vectors v and w. An orthogonal matrix is a square matrix. A square matrix a is orthogonal if its transpose. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix How to prove Orthogonal Is Matrix A An Orthogonal Matrix A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. An orthogonal matrix is a square matrix. Also, the product of an orthogonal matrix and its transpose is equal to i. a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. N (r) is orthogonal. Is Matrix A An Orthogonal Matrix.
From www.chegg.com
Solved For the matrix A, find an orthogonal matrix P such Is Matrix A An Orthogonal Matrix A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. a n×n matrix. Is Matrix A An Orthogonal Matrix.
From medium.com
[Linear Algebra] 9. Properties of orthogonal matrices by jun94 jun Is Matrix A An Orthogonal Matrix Also, the product of an orthogonal matrix and its transpose is equal to i. a matrix a ∈ gl. N (r) is orthogonal if av · aw = v · w for all vectors v and w. An orthogonal matrix is a square matrix. a matrix is an orthogonal matrix when the product of a matrix and its. Is Matrix A An Orthogonal Matrix.
From ar.inspiredpencil.com
Orthogonal Matrix Is Matrix A An Orthogonal Matrix An orthogonal matrix is a square matrix. N (r) is orthogonal if av · aw = v · w for all vectors v and w. Also, the product of an orthogonal matrix and its transpose is equal to i. In particular, taking v = w means that lengths. A square matrix a is orthogonal if its transpose a t is. Is Matrix A An Orthogonal Matrix.
From www.numerade.com
SOLVED Consider the matrix Find a basis of the orthogonal complement Is Matrix A An Orthogonal Matrix A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. Also, the product of an orthogonal matrix and its transpose is equal to i. In particular, taking v = w means that. Is Matrix A An Orthogonal Matrix.
From www.chegg.com
Solved a. Which of the matrices are orthogonal (has Is Matrix A An Orthogonal Matrix For a matrix 𝐴 to be orthogonal, it must be. Also, the product of an orthogonal matrix and its transpose is equal to i. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an. Is Matrix A An Orthogonal Matrix.
From teamlab.github.io
Basic Linear Algebra Is Matrix A An Orthogonal Matrix For a matrix 𝐴 to be orthogonal, it must be. N (r) is orthogonal if av · aw = v · w for all vectors v and w. In particular, taking v = w means that lengths. An orthogonal matrix is a square matrix. a matrix 'a' is orthogonal if and only if its inverse is equal to its. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
Orthogonal matrix with its properties Lecture 6 part 2 YouTube Is Matrix A An Orthogonal Matrix a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. a matrix a ∈ gl. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. For a matrix 𝐴 to be orthogonal, it must be. An orthogonal matrix is a square. Is Matrix A An Orthogonal Matrix.
From www.toppr.com
An orthogonal matrix is Maths Questions Is Matrix A An Orthogonal Matrix A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. Also, the product of an orthogonal matrix and its transpose is equal to i. For a matrix 𝐴 to be orthogonal, it must be. a matrix is an orthogonal matrix when the product of a matrix and its. Is Matrix A An Orthogonal Matrix.
From scoop.eduncle.com
Find orthogonal matrix and unitary matrix Is Matrix A An Orthogonal Matrix A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. Also, the product of an orthogonal matrix and its transpose is equal to i. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. For a matrix. Is Matrix A An Orthogonal Matrix.
From www.numerade.com
SOLVED Orthogonal Transformations Orthogonal Matrices In Exercises 12 Is Matrix A An Orthogonal Matrix An orthogonal matrix is a square matrix. In particular, taking v = w means that lengths. N (r) is orthogonal if av · aw = v · w for all vectors v and w. a matrix a ∈ gl. A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. A square. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
MATRICES (L3) LINEAR TRANSFORMATIONORTHOGONAL MATRIX YouTube Is Matrix A An Orthogonal Matrix A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. N (r) is orthogonal if av · aw = v · w for all. Is Matrix A An Orthogonal Matrix.
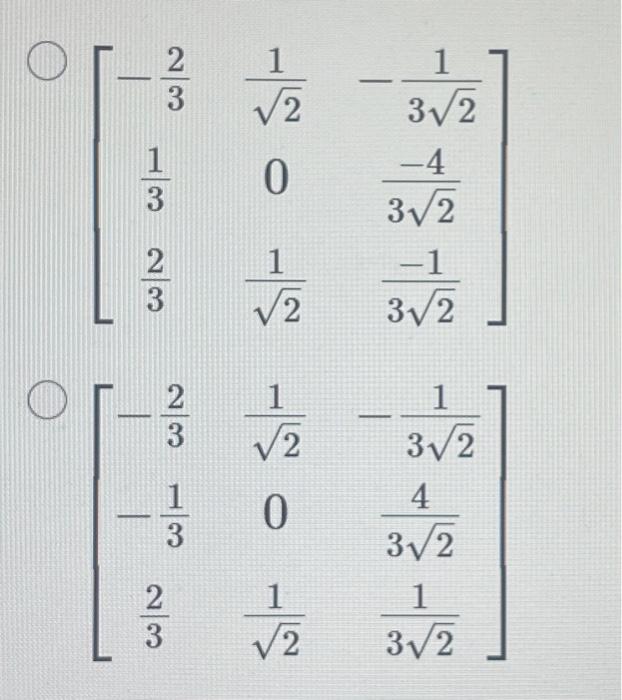
From www.coursehero.com
[Solved] . Fill in the missing values to make an orthogonal matrix. i Is Matrix A An Orthogonal Matrix a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. N (r) is orthogonal if av · aw = v · w for all vectors v and w. An orthogonal matrix is a square matrix. In particular, taking v = w means that lengths. a matrix 'a' is orthogonal. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
Linear Algebra Matrix Orthogonality YouTube Is Matrix A An Orthogonal Matrix In particular, taking v = w means that lengths. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. An orthogonal matrix is a square matrix. For a matrix 𝐴 to be orthogonal, it must be. A square matrix a is orthogonal if its transpose a t is also its. Is Matrix A An Orthogonal Matrix.
From datascienceparichay.com
Numpy Check If a Matrix is Orthogonal Data Science Parichay Is Matrix A An Orthogonal Matrix a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. N (r) is orthogonal if av · aw = v · w for all vectors v and w. An orthogonal matrix is a square matrix. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is. Is Matrix A An Orthogonal Matrix.
From dxofuolpl.blob.core.windows.net
Orthogonal Matrix And Orthonormal Matrix at Diane Fisher blog Is Matrix A An Orthogonal Matrix N (r) is orthogonal if av · aw = v · w for all vectors v and w. In particular, taking v = w means that lengths. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. Also, the product of an orthogonal matrix and its transpose is equal to. Is Matrix A An Orthogonal Matrix.
From ar.inspiredpencil.com
3x3 Orthogonal Matrix Is Matrix A An Orthogonal Matrix A square matrix a is orthogonal if its transpose a t is also its inverse a − 1. a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. N (r) is orthogonal if av · aw = v · w for all vectors v and w. For a matrix 𝐴 to be orthogonal,. Is Matrix A An Orthogonal Matrix.
From www.chegg.com
Solved Proceed as in this example to construct an orthogonal Is Matrix A An Orthogonal Matrix a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. An orthogonal matrix is a square matrix. a matrix a ∈ gl. For a matrix 𝐴 to be orthogonal, it must be. a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value.. Is Matrix A An Orthogonal Matrix.
From www.chegg.com
Solved 5. Find an orthogonal matrix Q and a diagonal matrix Is Matrix A An Orthogonal Matrix An orthogonal matrix is a square matrix. In particular, taking v = w means that lengths. a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For a matrix 𝐴 to be orthogonal, it must be. A square matrix a is orthogonal if its transpose a t is also its inverse a −. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
What is Orthogonal Matrix and its Properties Kamaldheeriya YouTube Is Matrix A An Orthogonal Matrix In particular, taking v = w means that lengths. Also, the product of an orthogonal matrix and its transpose is equal to i. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. a matrix a ∈ gl. a matrix 'a' is orthogonal. Is Matrix A An Orthogonal Matrix.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint Is Matrix A An Orthogonal Matrix An orthogonal matrix is a square matrix. Also, the product of an orthogonal matrix and its transpose is equal to i. A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
How to Prove that a Matrix is Orthogonal YouTube Is Matrix A An Orthogonal Matrix Also, the product of an orthogonal matrix and its transpose is equal to i. a matrix a ∈ gl. A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. In particular, taking v = w means that lengths. a n×n matrix a is an orthogonal matrix if. Is Matrix A An Orthogonal Matrix.
From www.slideserve.com
PPT Row and column matrices are sometimes called row vectors and Is Matrix A An Orthogonal Matrix a n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Also, the product of an orthogonal matrix and its transpose is equal to i. An orthogonal matrix is a square matrix. In particular, taking v = w means that lengths. a matrix 'a' is. Is Matrix A An Orthogonal Matrix.
From www.machinelearningplus.com
Linear Algebra Archives Machine Learning Plus Is Matrix A An Orthogonal Matrix a matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. a matrix a ∈ gl. A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. N (r) is orthogonal if av · aw = v · w for all vectors v. Is Matrix A An Orthogonal Matrix.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Is Matrix A An Orthogonal Matrix a matrix is an orthogonal matrix when the product of a matrix and its transpose gives an identity value. An orthogonal matrix is a square matrix. In particular, taking v = w means that lengths. Also, the product of an orthogonal matrix and its transpose is equal to i. A square matrix 𝐴 is orthogonal if 𝐴 𝐴 =. Is Matrix A An Orthogonal Matrix.
From dxooubuml.blob.core.windows.net
What Is A Orthogonal Matrix Definition at Richard Spencer blog Is Matrix A An Orthogonal Matrix Also, the product of an orthogonal matrix and its transpose is equal to i. In particular, taking v = w means that lengths. A square matrix 𝐴 is orthogonal if 𝐴 𝐴 = 𝐼 , where 𝐼 is the 𝑛 × 𝑛 identity matrix. a matrix a ∈ gl. N (r) is orthogonal if av · aw = v. Is Matrix A An Orthogonal Matrix.