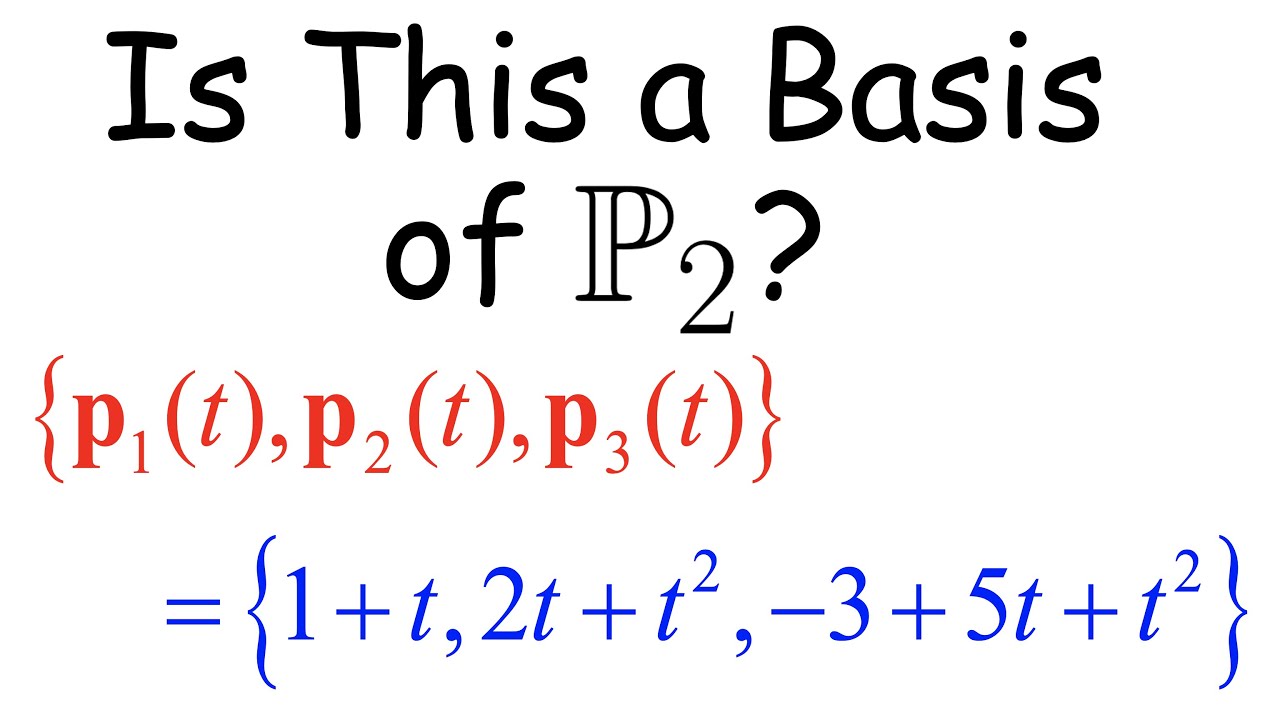Standard Bases Of R3 . — form a basis for \(\mathbb{r}^n \). In particular, \(\mathbb{r}^n \) has dimension \(n\). — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. Standard basis vectors are always. So if x = (x, y, z). This is sometimes known as the standard basis. Note if three vectors are linearly. The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0), and e3 = (0, 0, 1) e 3 = (0, 0, 1). — find the matrix of a linear transformation with respect to the standard basis. Thus = fi;j;kgis the standard basis for r3. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. Determine the action of a linear.
from www.youtube.com
— find the matrix of a linear transformation with respect to the standard basis. So if x = (x, y, z). In particular, \(\mathbb{r}^n \) has dimension \(n\). The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0), and e3 = (0, 0, 1) e 3 = (0, 0, 1). Standard basis vectors are always. Determine the action of a linear. Note if three vectors are linearly. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. — form a basis for \(\mathbb{r}^n \).
Basis Examples for Vector Spaces R^3 and Pn (Linear Independence and
Standard Bases Of R3 Standard basis vectors are always. This is sometimes known as the standard basis. Standard basis vectors are always. — form a basis for \(\mathbb{r}^n \). The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0), and e3 = (0, 0, 1) e 3 = (0, 0, 1). — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. Note if three vectors are linearly. Determine the action of a linear. In particular, \(\mathbb{r}^n \) has dimension \(n\). — find the matrix of a linear transformation with respect to the standard basis. Thus = fi;j;kgis the standard basis for r3. So if x = (x, y, z).
From www.chegg.com
Solved Let E be the standard basis of R3 and another basis Standard Bases Of R3 In particular, \(\mathbb{r}^n \) has dimension \(n\). — find the matrix of a linear transformation with respect to the standard basis. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0),. Standard Bases Of R3.
From www.youtube.com
Finding a Standard Matrix Using the Standard Basis YouTube Standard Bases Of R3 So if x = (x, y, z). This is sometimes known as the standard basis. Note if three vectors are linearly. Standard basis vectors are always. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1,. Standard Bases Of R3.
From www.chegg.com
Solved 3. Basis of R3 Given the vectors B C A 2 D 1 1 = 2 Standard Bases Of R3 Thus = fi;j;kgis the standard basis for r3. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. — find the matrix of a linear transformation with respect to the standard basis. — form a basis for \(\mathbb{r}^n \). distinguish bases (‘bases’ is the. Standard Bases Of R3.
From www.numerade.com
SOLVED Let e1, e2, e3 be the standard basis vectors in R3 and consider Standard Bases Of R3 Standard basis vectors are always. This is sometimes known as the standard basis. Note if three vectors are linearly. — find the matrix of a linear transformation with respect to the standard basis. The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0),. Standard Bases Of R3.
From www.chegg.com
Solved (a) (3 points) Let TR3 + R2 be the linear map Standard Bases Of R3 distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. Thus = fi;j;kgis the standard basis for r3. Determine the action of a linear. — form a basis for \(\mathbb{r}^n \). So if x = (x, y, z). — find the matrix of a linear transformation with respect to the standard basis. The. Standard Bases Of R3.
From www.chegg.com
Solved 1. Let 0 01 be the ordered standard basis in R3, and Standard Bases Of R3 Thus = fi;j;kgis the standard basis for r3. Note if three vectors are linearly. Determine the action of a linear. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1,. Standard Bases Of R3.
From www.numerade.com
Find a standard basis vector for R^3 that can be added to the set {𝐯1 Standard Bases Of R3 — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. In particular, \(\mathbb{r}^n \) has dimension \(n\). — find the matrix of a linear transformation with respect to the standard basis. So if x = (x, y, z). distinguish bases (‘bases’ is the plural of. Standard Bases Of R3.
From www.chegg.com
Solved Let B be the following ordered bases of R3 023 and Standard Bases Of R3 — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. Determine the action of a linear. Standard basis vectors are always. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. So if x = (x, y, z). — form a. Standard Bases Of R3.
From www.chegg.com
Solved 3. The standard basis in R3 consists of the vectors Standard Bases Of R3 distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. Note if three vectors are linearly. — find the matrix of a linear transformation with respect to the standard basis. Determine the action of a linear. — form a basis for \(\mathbb{r}^n \). — a standard basis, also called a natural basis,. Standard Bases Of R3.
From www.chegg.com
Solved Let {e1,e2,e3} be the standard basis of R3. If Standard Bases Of R3 Determine the action of a linear. Thus = fi;j;kgis the standard basis for r3. So if x = (x, y, z). distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. Standard basis vectors are always. — form a basis for \(\mathbb{r}^n \). Note if three vectors are linearly. In particular, \(\mathbb{r}^n \) has. Standard Bases Of R3.
From www.chegg.com
Solved Let {e1,e2, e3} be the standard basis of R3. If T R3 Standard Bases Of R3 In particular, \(\mathbb{r}^n \) has dimension \(n\). — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. This is sometimes known as the standard basis. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. Determine the action of a linear. The. Standard Bases Of R3.
From www.chegg.com
Solved Consider the following "standard" basis of R3 over R Standard Bases Of R3 The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0), and e3 = (0, 0, 1) e 3 = (0, 0, 1). Determine the action of a linear. Note if three vectors are linearly. In particular, \(\mathbb{r}^n \) has dimension \(n\). — a. Standard Bases Of R3.
From calcworkshop.com
Basis of Vector Spaces (A Linear Algebra Guide) Standard Bases Of R3 — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. This is sometimes known as the standard basis. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. — find the matrix of a linear transformation with respect to the standard. Standard Bases Of R3.
From www.chegg.com
Solved Consider the following "standard" basis of R3 over R Standard Bases Of R3 In particular, \(\mathbb{r}^n \) has dimension \(n\). So if x = (x, y, z). — form a basis for \(\mathbb{r}^n \). distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. Determine the action of a linear. Note if three vectors are linearly. — a standard basis, also called a natural basis, is. Standard Bases Of R3.
From www.chegg.com
Solved Let epsilon be the standard basis for R^3, and let B Standard Bases Of R3 This is sometimes known as the standard basis. In particular, \(\mathbb{r}^n \) has dimension \(n\). Standard basis vectors are always. — form a basis for \(\mathbb{r}^n \). The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0), and e3 = (0, 0, 1). Standard Bases Of R3.
From www.chegg.com
Solved 10. Let 1M 0 be the standard basis of R3. Consider Standard Bases Of R3 Thus = fi;j;kgis the standard basis for r3. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. Note if three vectors are linearly. — find the matrix of a linear transformation with respect to the standard basis. So if x = (x, y, z). In particular, \(\mathbb{r}^n \) has dimension \(n\). —. Standard Bases Of R3.
From www.youtube.com
Basis Examples for Vector Spaces R^3 and Pn (Linear Independence and Standard Bases Of R3 Thus = fi;j;kgis the standard basis for r3. — form a basis for \(\mathbb{r}^n \). So if x = (x, y, z). This is sometimes known as the standard basis. — find the matrix of a linear transformation with respect to the standard basis. Note if three vectors are linearly. — a standard basis, also called a. Standard Bases Of R3.
From www.chegg.com
Solved Let. S = (e1, e2, e3) 1m; the standard basis of R3. Standard Bases Of R3 Standard basis vectors are always. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. This is sometimes known as the standard basis. So if x = (x, y, z). Note if three vectors are linearly. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each. Standard Bases Of R3.
From www.chegg.com
Solved Problem 11. Let S denote the standard basis of R3. Standard Bases Of R3 This is sometimes known as the standard basis. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. So if x = (x, y, z). Thus = fi;j;kgis the standard basis for r3. — find the matrix of a linear transformation with respect to the standard. Standard Bases Of R3.
From www.numerade.com
SOLVED Let E be the standard basis of R3 and another basis given by B Standard Bases Of R3 In particular, \(\mathbb{r}^n \) has dimension \(n\). Note if three vectors are linearly. — form a basis for \(\mathbb{r}^n \). Standard basis vectors are always. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each. Standard Bases Of R3.
From www.chegg.com
Solved Let S = {ei,e2,c3} be the standard basis of R3. (a) Standard Bases Of R3 — form a basis for \(\mathbb{r}^n \). Standard basis vectors are always. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. In particular, \(\mathbb{r}^n \) has dimension \(n\). Determine the action of a linear. Thus = fi;j;kgis the standard basis for r3. This is sometimes known as the standard basis. So if x. Standard Bases Of R3.
From www.chegg.com
Solved Let ei 1 0 0 0 e2 0 be the standard basis of R3 and Standard Bases Of R3 distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. — form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. Standard basis vectors are always. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. Thus. Standard Bases Of R3.
From www.chegg.com
Solved 2. Let T R3 → R3 be the linear transformation Standard Bases Of R3 — find the matrix of a linear transformation with respect to the standard basis. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. Standard basis vectors are always. So if x = (x, y, z). This is sometimes known as the standard basis. distinguish. Standard Bases Of R3.
From www.numerade.com
Find a standard basis vector for R^{3} that can b… Standard Bases Of R3 Determine the action of a linear. The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0), and e3 = (0, 0, 1) e 3 = (0, 0, 1). Thus = fi;j;kgis the standard basis for r3. Note if three vectors are linearly. This is. Standard Bases Of R3.
From www.chegg.com
Solved Let B be the following ordered bases of R3 ( [0] Standard Bases Of R3 The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0), and e3 = (0, 0, 1) e 3 = (0, 0, 1). Standard basis vectors are always. So if x = (x, y, z). — form a basis for \(\mathbb{r}^n \). Note if. Standard Bases Of R3.
From www.youtube.com
Linear Algebra Check if a set is a basis of R^3 YouTube Standard Bases Of R3 Standard basis vectors are always. So if x = (x, y, z). The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0), and e3 = (0, 0, 1) e 3 = (0, 0, 1). — form a basis for \(\mathbb{r}^n \). In particular,. Standard Bases Of R3.
From www.chegg.com
Solved Let B=(e1,e2,e3) be the standard basis of R3 and Standard Bases Of R3 In particular, \(\mathbb{r}^n \) has dimension \(n\). — find the matrix of a linear transformation with respect to the standard basis. Thus = fi;j;kgis the standard basis for r3. Standard basis vectors are always. — form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. — a standard basis, also called a natural. Standard Bases Of R3.
From www.chegg.com
Solved Let {e1,e2, e3} be the standard basis of R3. If T R3 Standard Bases Of R3 So if x = (x, y, z). In particular, \(\mathbb{r}^n \) has dimension \(n\). Note if three vectors are linearly. The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0, 1, 0), and e3 = (0, 0, 1) e 3 = (0, 0, 1). Determine the. Standard Bases Of R3.
From www.youtube.com
Ejemplo 3 Base de R3 YouTube Standard Bases Of R3 Standard basis vectors are always. Note if three vectors are linearly. In particular, \(\mathbb{r}^n \) has dimension \(n\). — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. So if x = (x, y, z). Thus = fi;j;kgis the standard basis for r3. — find the. Standard Bases Of R3.
From www.numerade.com
SOLVED (4 points) Find standard basis vector for R3 that can be added Standard Bases Of R3 — find the matrix of a linear transformation with respect to the standard basis. Standard basis vectors are always. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. —. Standard Bases Of R3.
From www.youtube.com
vector spaces /Standard basis / Subspaces of R2, R3 /Translation Standard Bases Of R3 — form a basis for \(\mathbb{r}^n \). So if x = (x, y, z). distinguish bases (‘bases’ is the plural of ‘basis’) from other subsets of a set. Determine the action of a linear. Thus = fi;j;kgis the standard basis for r3. — find the matrix of a linear transformation with respect to the standard basis. Standard. Standard Bases Of R3.
From www.chegg.com
Solved (1 point) Suppose T R3 → R3 is a linear Standard Bases Of R3 — find the matrix of a linear transformation with respect to the standard basis. Determine the action of a linear. In particular, \(\mathbb{r}^n \) has dimension \(n\). — form a basis for \(\mathbb{r}^n \). The standard basis is e1 = (1, 0, 0) e 1 = (1, 0, 0), e2 = (0, 1, 0) e 2 = (0,. Standard Bases Of R3.
From www.coursehero.com
[Solved] A. Let S be the standard basis of R^3 and T be the set of Standard Bases Of R3 Standard basis vectors are always. — form a basis for \(\mathbb{r}^n \). Note if three vectors are linearly. This is sometimes known as the standard basis. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. distinguish bases (‘bases’ is the plural of ‘basis’) from. Standard Bases Of R3.
From www.numerade.com
SOLVED Let E be the standard basis of R3 and another basis given by B Standard Bases Of R3 Determine the action of a linear. This is sometimes known as the standard basis. — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. Standard basis vectors are always. — form a basis for \(\mathbb{r}^n \). Note if three vectors are linearly. distinguish bases (‘bases’. Standard Bases Of R3.
From www.chegg.com
Solved 10. Let be the standard basis of R3. Consider the Standard Bases Of R3 Standard basis vectors are always. Determine the action of a linear. In particular, \(\mathbb{r}^n \) has dimension \(n\). — a standard basis, also called a natural basis, is a special orthonormal vector basis in which each basis vector has a. So if x = (x, y, z). This is sometimes known as the standard basis. Thus = fi;j;kgis the. Standard Bases Of R3.