Calculate Gradient Numerically at Elijah Gore blog

Calculate Gradient Numerically. Then you could approximate the partial derivatives directly, and assemble them into the gradient vector. In this post, we'll explore. A way better approach (numerically more stable, no issue of choosing the perturbation hyperparameter, accurate up to machine. The gradient can be thought of as a collection of vectors pointing in the direction of increasing values of f. For a function of two variables, f (x, y), the gradient is. G(x, y) = df/dx i + df/dy j where (i, j) are unit vectors in x and y. I know the gradient of a function t on a cartesian grid: I know t for the center pillar:. The steepest (or gradient) descent method is one such iterative procedure to approximate extreme values. It is based on the fact that the gradient gives the steepest. The only way to calculate gradient is calculus. One of its many useful features is the ability to calculate numerical gradients of functions using the gradient function. ∇f = ∂f ∂xˆ i +∂f ∂ yˆ j. G (xi, yj, zk) = ∇t(xi, yj, zk) g → (x i, y j, z k) = ∇ t (x i, y j, z k).

I know the gradient of a function t on a cartesian grid: A way better approach (numerically more stable, no issue of choosing the perturbation hyperparameter, accurate up to machine. The steepest (or gradient) descent method is one such iterative procedure to approximate extreme values. In this post, we'll explore. G (xi, yj, zk) = ∇t(xi, yj, zk) g → (x i, y j, z k) = ∇ t (x i, y j, z k). ∇f = ∂f ∂xˆ i +∂f ∂ yˆ j. The only way to calculate gradient is calculus. The gradient can be thought of as a collection of vectors pointing in the direction of increasing values of f. G(x, y) = df/dx i + df/dy j where (i, j) are unit vectors in x and y. One of its many useful features is the ability to calculate numerical gradients of functions using the gradient function.

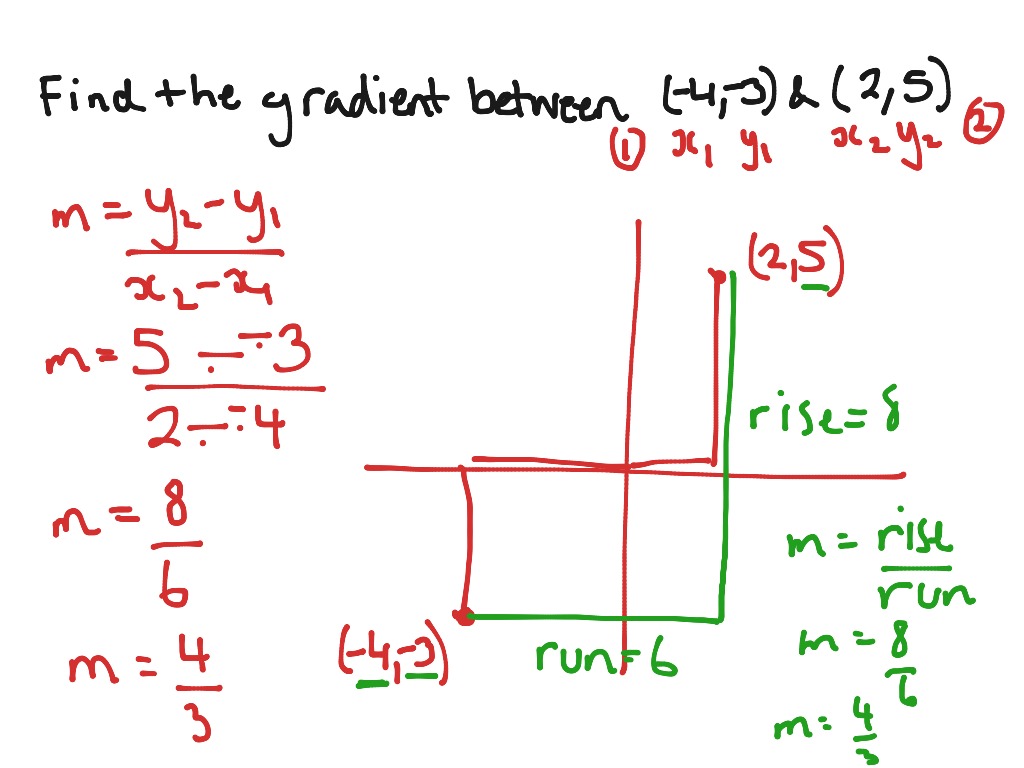
Finding the gradient between two points Math ShowMe

Calculate Gradient Numerically ∇f = ∂f ∂xˆ i +∂f ∂ yˆ j. ∇f = ∂f ∂xˆ i +∂f ∂ yˆ j. I know the gradient of a function t on a cartesian grid: Then you could approximate the partial derivatives directly, and assemble them into the gradient vector. The gradient can be thought of as a collection of vectors pointing in the direction of increasing values of f. G (xi, yj, zk) = ∇t(xi, yj, zk) g → (x i, y j, z k) = ∇ t (x i, y j, z k). The only way to calculate gradient is calculus. The steepest (or gradient) descent method is one such iterative procedure to approximate extreme values. A way better approach (numerically more stable, no issue of choosing the perturbation hyperparameter, accurate up to machine. One of its many useful features is the ability to calculate numerical gradients of functions using the gradient function. In this post, we'll explore. For a function of two variables, f (x, y), the gradient is. It is based on the fact that the gradient gives the steepest. I know t for the center pillar:. G(x, y) = df/dx i + df/dy j where (i, j) are unit vectors in x and y.