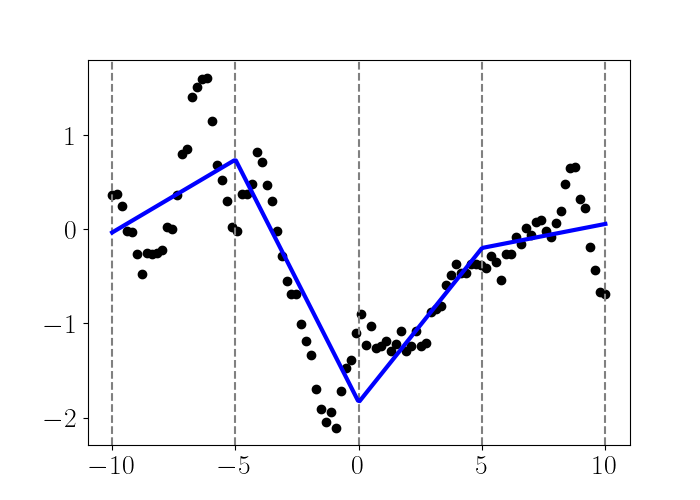
Linear Regression Vs Spline . Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. With enough knots, cubic spline regression can work very well. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Polynomial regression# splines can fit complex functions with few parameters. Within each region, a polynomial function (also called a basis spline or b. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials;
from andrewcharlesjones.github.io
However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. With enough knots, cubic spline regression can work very well. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Within each region, a polynomial function (also called a basis spline or b. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Polynomial regression# splines can fit complex functions with few parameters.
Andy Jones
Linear Regression Vs Spline Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). With enough knots, cubic spline regression can work very well. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Within each region, a polynomial function (also called a basis spline or b. Polynomial regression# splines can fit complex functions with few parameters. However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the.
From www.researchgate.net
An example of a piecewise linear regression spline, the fundamental Linear Regression Vs Spline Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x.. Linear Regression Vs Spline.
From bookdown.org
Chapter 9 Splines Machine Learning Linear Regression Vs Spline Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Polynomial regression# splines can fit complex functions with few parameters. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines and smoothing splines are motivated. Linear Regression Vs Spline.
From lbelzile.github.io
9 Splines lineaRmodels Linear Regression Vs Spline Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines and. Linear Regression Vs Spline.
From www.r-bloggers.com
Understanding Spline Regression Rbloggers Linear Regression Vs Spline Within each region, a polynomial function (also called a basis spline or b. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; With enough knots, cubic spline regression can work very well. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Piecewise regression. Linear Regression Vs Spline.
From datavalley.ai
Linear Regression Vs Logistic Regression Datavalley Linear Regression Vs Spline Within each region, a polynomial function (also called a basis spline or b. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Instead of a single regression line, we fit a set of piecewise linear regressions. Linear Regression Vs Spline.
From slidetodoc.com
Chapter 16 Curve Fitting Splines Spline Interpolation z Linear Regression Vs Spline With enough knots, cubic spline regression can work very well. Polynomial regression# splines can fit complex functions with few parameters. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Regression splines involve dividing the range of a feature x. Linear Regression Vs Spline.
From www.r-bloggers.com
Plot_ss in R. Smoothing splines and polynomial regression plots R Linear Regression Vs Spline Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Within each region, a polynomial function (also called a basis spline or b. Polynomial regression# splines can fit complex functions with few parameters. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they. Linear Regression Vs Spline.
From coding-blocks.github.io
Linear Regression — Data Science Notes Linear Regression Vs Spline Within each region, a polynomial function (also called a basis spline or b. With enough knots, cubic spline regression can work very well. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they. Linear Regression Vs Spline.
From www.statology.org
How to Perform Spline Regression in R (With Example) Linear Regression Vs Spline However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). With enough knots, cubic spline regression can work very well. Instead of a single regression line, we fit a set of piecewise linear regressions. Linear Regression Vs Spline.
From www.askpython.com
Regression Splines in Python A Beginners Introduction AskPython Linear Regression Vs Spline Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Within each region, a polynomial function (also called a basis spline or b. However, like with polynomial. Linear Regression Vs Spline.
From kirenz.github.io
Regression splines — Introduction to Regression Models Linear Regression Vs Spline Polynomial regression# splines can fit complex functions with few parameters. With enough knots, cubic spline regression can work very well. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials;. Linear Regression Vs Spline.
From bookdown.org
2 Piecewise Regression and Splines Machine Learning for Biostatistics Linear Regression Vs Spline Polynomial regression# splines can fit complex functions with few parameters. Within each region, a polynomial function (also called a basis spline or b. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines and smoothing splines are motivated from a different perspective than kernels. Linear Regression Vs Spline.
From www.researchgate.net
Penalized splines regression and linear regression of DMA on Linear Regression Vs Spline Within each region, a polynomial function (also called a basis spline or b. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. However, like with polynomial regression, the system sometimes works. Linear Regression Vs Spline.
From www.linkedin.com
Understanding Linear Regression The Basics Linear Regression Vs Spline Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Polynomial regression# splines can fit complex functions with few parameters. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Instead. Linear Regression Vs Spline.
From bookdown.org
Chapter 9 Splines Machine Learning Linear Regression Vs Spline Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Instead of a single regression line, we fit a set. Linear Regression Vs Spline.
From www.researchgate.net
Penalized splines regression and linear regression of DMA on Linear Regression Vs Spline Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Polynomial regression# splines can fit complex functions with few parameters. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Within. Linear Regression Vs Spline.
From towardsdatascience.com
MARS Multivariate Adaptive Regression Splines — How to Improve on Linear Regression Vs Spline Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Within each region, a polynomial function (also called a basis spline or b. With enough knots, cubic. Linear Regression Vs Spline.
From dmpeli.math.mcmaster.ca
Lecture 23 Linear and cubic splines Linear Regression Vs Spline With enough knots, cubic spline regression can work very well. However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Piecewise regression yields continuous functions which are not, generally,. Linear Regression Vs Spline.
From www.andreaperlato.com
Polynomial Regression & Smoothing Splines Andrea Perlato Linear Regression Vs Spline Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Within each region, a polynomial function (also called a basis spline or b. With enough knots, cubic spline regression can work very well. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Polynomial regression# splines can fit complex functions. Linear Regression Vs Spline.
From www.researchgate.net
Estimation of multivariable linear spline regression models with Linear Regression Vs Spline With enough knots, cubic spline regression can work very well. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Polynomial regression# splines can fit complex functions with few parameters. However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Regression splines and smoothing splines are motivated from a. Linear Regression Vs Spline.
From towardsdatascience.com
Linear Regression Explained. A High Level Overview of Linear… by Linear Regression Vs Spline Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. With enough knots,. Linear Regression Vs Spline.
From www.youtube.com
Polynomial Regression and Splines YouTube Linear Regression Vs Spline Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Within each region, a polynomial function (also called a basis spline or b. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; However, like with polynomial regression, the system sometimes works very poorly at. Linear Regression Vs Spline.
From patsy.readthedocs.io
Spline regression — patsy 0.5.1+dev documentation Linear Regression Vs Spline Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. With enough knots, cubic spline regression can work very well. Polynomial regression# splines. Linear Regression Vs Spline.
From www.jmp.com
Multiple Linear Regression Introduction to Statistics JMP Linear Regression Vs Spline However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). With enough knots, cubic spline regression can work very well. Polynomial regression# splines can fit complex functions with few parameters. Instead of a single. Linear Regression Vs Spline.
From stats.stackexchange.com
regression How to get from cubic spline to natural cubic spline Linear Regression Vs Spline Within each region, a polynomial function (also called a basis spline or b. With enough knots, cubic spline regression can work very well. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Instead. Linear Regression Vs Spline.
From patsy.readthedocs.io
Spline regression — patsy 0.5.1+dev documentation Linear Regression Vs Spline Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Polynomial regression# splines can fit complex functions with few parameters. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth.. Linear Regression Vs Spline.
From onlineengineeringnotes.com
Interpolation and Approximation Numerical Differentiation and Linear Regression Vs Spline Within each region, a polynomial function (also called a basis spline or b. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines involve dividing the range of a feature. Linear Regression Vs Spline.
From andrewcharlesjones.github.io
Andy Jones Linear Regression Vs Spline Polynomial regression# splines can fit complex functions with few parameters. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; However,. Linear Regression Vs Spline.
From biostat2.uni.lu
Regression linear models Linear Regression Vs Spline Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Within each region, a polynomial function (also called a basis spline or b. Instead of a single regression line, we fit a set of piecewise linear regressions with the. Linear Regression Vs Spline.
From www.youtube.com
Linear Spline Interpolation Numerical Computation YouTube Linear Regression Vs Spline Within each region, a polynomial function (also called a basis spline or b. However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Instead of a single regression line, we fit a set of. Linear Regression Vs Spline.
From www.r-bloggers.com
Understanding Spline Regression Rbloggers Linear Regression Vs Spline Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. With enough knots, cubic spline. Linear Regression Vs Spline.
From www.researchgate.net
8 Comparing Smoothing splines (Ssplines), hybrid splines (Hsplines Linear Regression Vs Spline With enough knots, cubic spline regression can work very well. Piecewise regression yields continuous functions which are not, generally, differentiable and hence not smooth. Polynomial regression# splines can fit complex functions with few parameters. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Instead of a single regression line, we fit a set. Linear Regression Vs Spline.
From statisticsr.blogspot.com
Experience with R notes for Polynomial Regression, Splines and GAM Linear Regression Vs Spline Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Polynomial regression# splines can fit complex functions with few parameters. With enough knots, cubic spline regression can. Linear Regression Vs Spline.
From www.lennysnewsletter.com
How to do linear regression and correlation analysis Linear Regression Vs Spline With enough knots, cubic spline regression can work very well. However, like with polynomial regression, the system sometimes works very poorly at the outer ranges of x. Instead of a single regression line, we fit a set of piecewise linear regressions with the only restriction being that they intersect at the. Regression splines involve dividing the range of a feature. Linear Regression Vs Spline.
From bradleyboehmke.github.io
Chapter 7 Multivariate Adaptive Regression Splines HandsOn Machine Linear Regression Vs Spline Within each region, a polynomial function (also called a basis spline or b. Regression splines and smoothing splines are motivated from a different perspective than kernels and local polynomials; Polynomial regression# splines can fit complex functions with few parameters. Regression splines involve dividing the range of a feature x into k distinct regions (by using so called knots). Piecewise regression. Linear Regression Vs Spline.