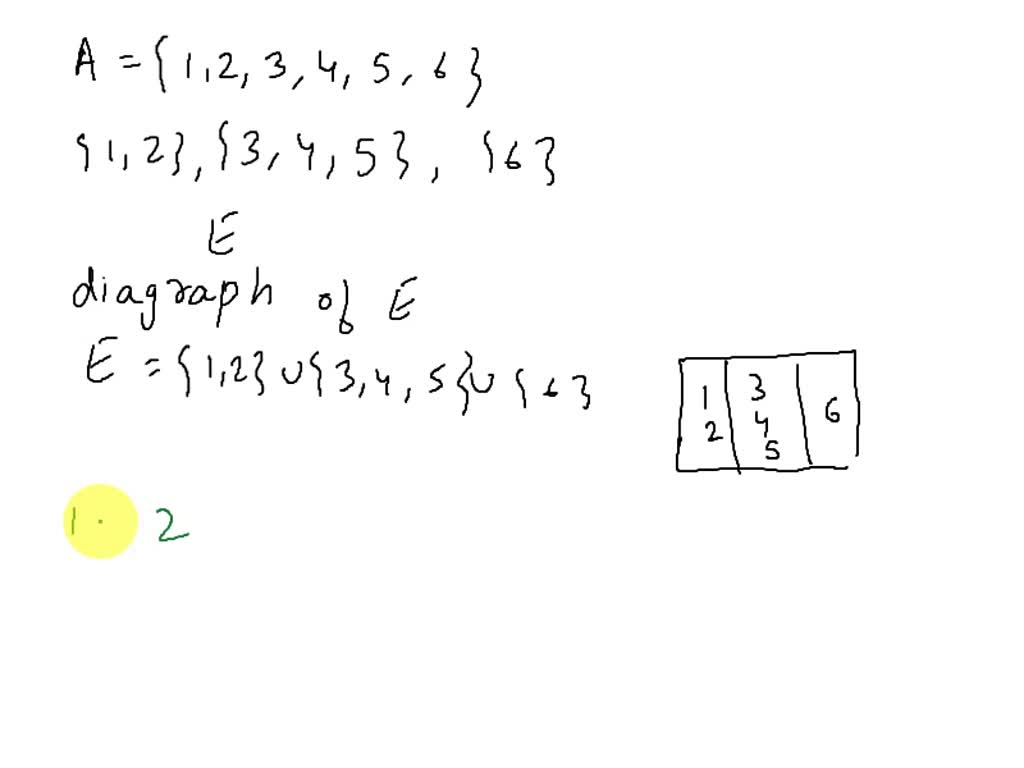Equivalence Classes Form A Partition . All this means that the equivalence classes form a partition of $s$. In each equivalence class, all the elements are. Given an equivalence relation we can prove that its equivalence classes form a set partition. We can de ne a relation r by r(a; Congruence modulo \ (n\) and congruence classes. There are many other examples at hand,. If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Let x = y = z. Any partition p has a corresponding equivalence relation. Equivalence classes are a type of partition, but not all partitions are equivalence classes. For any equivalence relation on a set the set of all its equivalence classes is a partition of. Learn about their definition, properties, and practical examples. The definition of an equivalence class. The converse is also true. Given a partition on set.
from www.numerade.com
Learn about their definition, properties, and practical examples. We can de ne a relation r by r(x; If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Let \(r\) be an equivalence relation on \(a\text{.}\) All this means that the equivalence classes form a partition of $s$. The converse is also true. For any equivalence relation on a set the set of all its equivalence classes is a partition of. Specifically, we define x ∼ y if and only if x and y are in the same element of p. There are many other examples at hand,. Any partition p has a corresponding equivalence relation.
SOLVED (5) Let A = 1,2,3,4,5,6. The sets 1,2, 3,4,5, and 6 form a
Equivalence Classes Form A Partition Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. Equivalence classes are a type of partition, but not all partitions are equivalence classes. Given an equivalence relation we can prove that its equivalence classes form a set partition. We can de ne a relation r by r(a; Given a partition on set. All this means that the equivalence classes form a partition of $s$. There are many other examples at hand,. If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Let x = y = z. Specifically, we define x ∼ y if and only if x and y are in the same element of p. Learn about their definition, properties, and practical examples. For any equivalence relation on a set the set of all its equivalence classes is a partition of. Any partition p has a corresponding equivalence relation. The definition of an equivalence class. In each equivalence class, all the elements are. We can de ne a relation r by r(x;
From www.youtube.com
The Equivalence Classes of A form a set partition of A. YouTube Equivalence Classes Form A Partition We can de ne a relation r by r(x; Given a partition on set. Equivalence classes are a type of partition, but not all partitions are equivalence classes. Let x = y = z. The definition of an equivalence class. All this means that the equivalence classes form a partition of $s$. Any partition p has a corresponding equivalence relation.. Equivalence Classes Form A Partition.
From www.studypool.com
SOLUTION Partition equivalence classes Studypool Equivalence Classes Form A Partition Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. Congruence modulo \ (n\) and congruence classes. All this means that the equivalence classes form a partition of $s$. The converse is also true. The definition of an equivalence class. In each equivalence class, all the elements are. Given an equivalence relation we can prove that its equivalence classes. Equivalence Classes Form A Partition.
From www.youtube.com
Manual Testing Equivalence class partitioning YouTube Equivalence Classes Form A Partition Learn about their definition, properties, and practical examples. Given a partition on set. We can de ne a relation r by r(a; If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Let \(r\) be an equivalence relation on \(a\text{.}\) Congruence modulo \ (n\) and congruence classes. The definition of an equivalence. Equivalence Classes Form A Partition.
From www.selmanalpdundar.com
Equivalence Class Partitioning and Boundary Value Analysis Example Equivalence Classes Form A Partition Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. Equivalence classes are a type of partition, but not all partitions are equivalence classes. We can de ne a relation r by r(a; The converse is also true. For any equivalence relation on a set the set of all its equivalence classes is a partition of. The definition of. Equivalence Classes Form A Partition.
From www.slideserve.com
PPT Closures of Relations Transitive Closure and Equivalence Equivalence Classes Form A Partition We can de ne a relation r by r(a; In each equivalence class, all the elements are. Specifically, we define x ∼ y if and only if x and y are in the same element of p. Given a partition on set. The converse is also true. Learn about their definition, properties, and practical examples. Conversely, given a partition of. Equivalence Classes Form A Partition.
From www.youtube.com
Equivalence Relations & Set Partitions, Part One YouTube Equivalence Classes Form A Partition In each equivalence class, all the elements are. Let x = y = z. Any partition p has a corresponding equivalence relation. Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. We can de ne a relation r by r(a; The definition of an equivalence class. Congruence modulo \ (n\) and congruence classes. Let \(r\) be an equivalence. Equivalence Classes Form A Partition.
From www.youtube.com
Prove that the distinct equivalence classes of an equivalence relation Equivalence Classes Form A Partition In each equivalence class, all the elements are. Given an equivalence relation we can prove that its equivalence classes form a set partition. There are many other examples at hand,. Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. Let \(r\) be an equivalence relation on \(a\text{.}\) All this means that the equivalence classes form a partition of. Equivalence Classes Form A Partition.
From slideplayer.com
Equivalence Relations ppt download Equivalence Classes Form A Partition Congruence modulo \ (n\) and congruence classes. Specifically, we define x ∼ y if and only if x and y are in the same element of p. For any equivalence relation on a set the set of all its equivalence classes is a partition of. Equivalence classes are a type of partition, but not all partitions are equivalence classes. Learn. Equivalence Classes Form A Partition.
From slideplayer.com
Lecture 12 NonRegular Languages ppt download Equivalence Classes Form A Partition Congruence modulo \ (n\) and congruence classes. Equivalence classes are a type of partition, but not all partitions are equivalence classes. Learn about their definition, properties, and practical examples. Given an equivalence relation we can prove that its equivalence classes form a set partition. There are many other examples at hand,. Let \(r\) be an equivalence relation on \(a\text{.}\) If. Equivalence Classes Form A Partition.
From www.youtube.com
Equivalence Classes Partition a Set Proof YouTube Equivalence Classes Form A Partition Learn about their definition, properties, and practical examples. There are many other examples at hand,. We can de ne a relation r by r(x; Specifically, we define x ∼ y if and only if x and y are in the same element of p. All this means that the equivalence classes form a partition of $s$. Conversely, given a partition. Equivalence Classes Form A Partition.
From slideplayer.com
Equivalence Relations ppt download Equivalence Classes Form A Partition There are many other examples at hand,. Given an equivalence relation we can prove that its equivalence classes form a set partition. Specifically, we define x ∼ y if and only if x and y are in the same element of p. Equivalence classes are a type of partition, but not all partitions are equivalence classes. The definition of an. Equivalence Classes Form A Partition.
From slideplayer.com
Equivalence Relations ppt download Equivalence Classes Form A Partition Let x = y = z. In each equivalence class, all the elements are. Equivalence classes are a type of partition, but not all partitions are equivalence classes. Given an equivalence relation we can prove that its equivalence classes form a set partition. Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. Given a partition on set. Learn. Equivalence Classes Form A Partition.
From www.numerade.com
SOLVED Determine the equivalence classes for the relation of Equivalence Classes Form A Partition Given a partition on set. There are many other examples at hand,. Equivalence classes are a type of partition, but not all partitions are equivalence classes. Specifically, we define x ∼ y if and only if x and y are in the same element of p. In each equivalence class, all the elements are. We can de ne a relation. Equivalence Classes Form A Partition.
From www.youtube.com
Partitions and Equivalence classes YouTube Equivalence Classes Form A Partition The converse is also true. Equivalence classes are a type of partition, but not all partitions are equivalence classes. For any equivalence relation on a set the set of all its equivalence classes is a partition of. Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. Given a partition on set. We can de ne a relation r. Equivalence Classes Form A Partition.
From www.slideserve.com
PPT 8.5 Equivalence Relations PowerPoint Presentation, free download Equivalence Classes Form A Partition In each equivalence class, all the elements are. Equivalence classes are a type of partition, but not all partitions are equivalence classes. If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). The converse is also true. Let \(r\) be an equivalence relation on \(a\text{.}\) Congruence modulo \ (n\) and congruence classes.. Equivalence Classes Form A Partition.
From www.numerade.com
SOLVED (5) Let A = 1,2,3,4,5,6. The sets 1,2, 3,4,5, and 6 form a Equivalence Classes Form A Partition Given a partition on set. The definition of an equivalence class. Let \(r\) be an equivalence relation on \(a\text{.}\) In each equivalence class, all the elements are. Given an equivalence relation we can prove that its equivalence classes form a set partition. All this means that the equivalence classes form a partition of $s$. We can de ne a relation. Equivalence Classes Form A Partition.
From www.studypool.com
SOLUTION Partition equivalence classes Studypool Equivalence Classes Form A Partition For any equivalence relation on a set the set of all its equivalence classes is a partition of. Let \(r\) be an equivalence relation on \(a\text{.}\) Congruence modulo \ (n\) and congruence classes. There are many other examples at hand,. Given an equivalence relation we can prove that its equivalence classes form a set partition. The definition of an equivalence. Equivalence Classes Form A Partition.
From www.slideserve.com
PPT Equivalence Relations PowerPoint Presentation, free download ID Equivalence Classes Form A Partition If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). We can de ne a relation r by r(x; Given an equivalence relation we can prove that its equivalence classes form a set partition. Learn about their definition, properties, and practical examples. Let \(r\) be an equivalence relation on \(a\text{.}\) Equivalence classes. Equivalence Classes Form A Partition.
From slideplayer.com
Definition 2. 20 Let R be an equivalence relation on a set A ppt Equivalence Classes Form A Partition For any equivalence relation on a set the set of all its equivalence classes is a partition of. Let \(r\) be an equivalence relation on \(a\text{.}\) The converse is also true. Given an equivalence relation we can prove that its equivalence classes form a set partition. Specifically, we define x ∼ y if and only if x and y are. Equivalence Classes Form A Partition.
From www.youtube.com
Equivalence Classes and Partitions YouTube Equivalence Classes Form A Partition The definition of an equivalence class. Let x = y = z. Congruence modulo \ (n\) and congruence classes. Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. In each equivalence class, all the elements are. Given an equivalence relation we can prove that its equivalence classes form a set partition. The converse is also true. Learn about. Equivalence Classes Form A Partition.
From www.slideserve.com
PPT Equivalence Relations PowerPoint Presentation, free download ID Equivalence Classes Form A Partition All this means that the equivalence classes form a partition of $s$. Given an equivalence relation we can prove that its equivalence classes form a set partition. If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Given a partition on set. In each equivalence class, all the elements are. We can. Equivalence Classes Form A Partition.
From slideplayer.com
Equivalence Relations Selected Exercises ppt download Equivalence Classes Form A Partition All this means that the equivalence classes form a partition of $s$. Specifically, we define x ∼ y if and only if x and y are in the same element of p. For any equivalence relation on a set the set of all its equivalence classes is a partition of. If \(r\) is an equivalence relation on the set \(a\),. Equivalence Classes Form A Partition.
From www.slideserve.com
PPT Equivalence Partitioning PowerPoint Presentation, free download Equivalence Classes Form A Partition We can de ne a relation r by r(x; The converse is also true. Learn about their definition, properties, and practical examples. In each equivalence class, all the elements are. If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Congruence modulo \ (n\) and congruence classes. There are many other examples. Equivalence Classes Form A Partition.
From www.youtube.com
Equivalence Classes Quotient set Partition and Covering of sets Equivalence Classes Form A Partition Learn about their definition, properties, and practical examples. The converse is also true. The definition of an equivalence class. Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. There are many other examples at hand,. Given a partition on set. Let \(r\) be an equivalence relation on \(a\text{.}\) In each equivalence class, all the elements are. We can. Equivalence Classes Form A Partition.
From www.slideserve.com
PPT Equivalence Relations PowerPoint Presentation, free download ID Equivalence Classes Form A Partition There are many other examples at hand,. Given a partition on set. For any equivalence relation on a set the set of all its equivalence classes is a partition of. Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. We can de ne a relation r by r(a; If \(r\) is an equivalence relation on the set \(a\),. Equivalence Classes Form A Partition.
From www.youtube.com
Important Math Proof The Set of Equivalence Classes Partition a Set Equivalence Classes Form A Partition Congruence modulo \ (n\) and congruence classes. The definition of an equivalence class. Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. The converse is also true. In each equivalence class, all the elements are. We can de ne a relation r by r(a; We can de ne a relation r by r(x; Let x = y =. Equivalence Classes Form A Partition.
From slideplayer.com
CS100 Discrete structures ppt download Equivalence Classes Form A Partition The definition of an equivalence class. Equivalence classes are a type of partition, but not all partitions are equivalence classes. Given an equivalence relation we can prove that its equivalence classes form a set partition. Learn about their definition, properties, and practical examples. Congruence modulo \ (n\) and congruence classes. We can de ne a relation r by r(x; Any. Equivalence Classes Form A Partition.
From www.studypool.com
SOLUTION Equivalence relation partition cells and equivalence class Equivalence Classes Form A Partition Given a partition on set. The converse is also true. Let \(r\) be an equivalence relation on \(a\text{.}\) We can de ne a relation r by r(x; The definition of an equivalence class. If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Conversely, given a partition of $s$ in subsets $c_\lambda$,. Equivalence Classes Form A Partition.
From calcworkshop.com
Equivalence Relation (Defined w/ 17 StepbyStep Examples!) Equivalence Classes Form A Partition If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Learn about their definition, properties, and practical examples. The converse is also true. Let \(r\) be an equivalence relation on \(a\text{.}\) Given an equivalence relation we can prove that its equivalence classes form a set partition. Any partition p has a corresponding. Equivalence Classes Form A Partition.
From www.researchgate.net
Listing of equivalence class partitions for Module Resource Download Equivalence Classes Form A Partition Equivalence classes are a type of partition, but not all partitions are equivalence classes. All this means that the equivalence classes form a partition of $s$. The definition of an equivalence class. Learn about their definition, properties, and practical examples. Let x = y = z. Let \(r\) be an equivalence relation on \(a\text{.}\) The converse is also true. Conversely,. Equivalence Classes Form A Partition.
From www.youtube.com
Equivalence Classes and Partitions (Solved Problems) YouTube Equivalence Classes Form A Partition If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Let \(r\) be an equivalence relation on \(a\text{.}\) We can de ne a relation r by r(x; Given an equivalence relation we can prove that its equivalence classes form a set partition. Learn about their definition, properties, and practical examples. We can. Equivalence Classes Form A Partition.
From www.slideserve.com
PPT Equivalence Partitioning PowerPoint Presentation, free download Equivalence Classes Form A Partition Given a partition on set. Let \(r\) be an equivalence relation on \(a\text{.}\) We can de ne a relation r by r(x; If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). All this means that the equivalence classes form a partition of $s$. Congruence modulo \ (n\) and congruence classes. The. Equivalence Classes Form A Partition.
From slideplayer.com
Equivalence Relations Selected Exercises ppt download Equivalence Classes Form A Partition The definition of an equivalence class. Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. In each equivalence class, all the elements are. For any equivalence relation on a set the set of all its equivalence classes is a partition of. Given an equivalence relation we can prove that its equivalence classes form a set partition. Learn about. Equivalence Classes Form A Partition.
From www.studocu.com
IUM 13 Equivalence relations, equivalence classes, and partitions 1 Equivalence Classes Form A Partition The converse is also true. In each equivalence class, all the elements are. Learn about their definition, properties, and practical examples. Congruence modulo \ (n\) and congruence classes. If \(r\) is an equivalence relation on the set \(a\), its equivalence classes form a partition of \(a\). Conversely, given a partition of $s$ in subsets $c_\lambda$, define an. We can de. Equivalence Classes Form A Partition.
From www.slideserve.com
PPT Discrete Mathematics PowerPoint Presentation, free download ID Equivalence Classes Form A Partition Given a partition on set. We can de ne a relation r by r(a; Let \(r\) be an equivalence relation on \(a\text{.}\) For any equivalence relation on a set the set of all its equivalence classes is a partition of. Equivalence classes are a type of partition, but not all partitions are equivalence classes. There are many other examples at. Equivalence Classes Form A Partition.