Is The Set Of All Integers A Vector Space . For example, the set of integers from 1 1 through 5 5. (1) the set of $n \times n$ magic squares (with real. {0v} is a subspace of v (the zero subspace’’). Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. let z be the set of all integers. The sum of any two real numbers is a real number,. Example 1.4 gives a subset of an that. The set of real numbers is a vector space over itself: A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. a vector space is a subspace of itself. the set of all functions which are never zero \[\left\{ f \colon \re\rightarrow \re \mid f(x)\neq 0 {\rm ~for~any}~x\in\re. the following sets and associated operations are not vector spaces: a set is a collection of objects. some real vector spaces: The set of column vectors whose entries are.
from www.bartleby.com
a vector space is a subspace of itself. let z be the set of all integers. a set is a collection of objects. {0v} is a subspace of v (the zero subspace’’). The sum of any two real numbers is a real number,. the following sets and associated operations are not vector spaces: some real vector spaces: A vector space is a set of elements (called. A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. For example, the set of integers from 1 1 through 5 5.
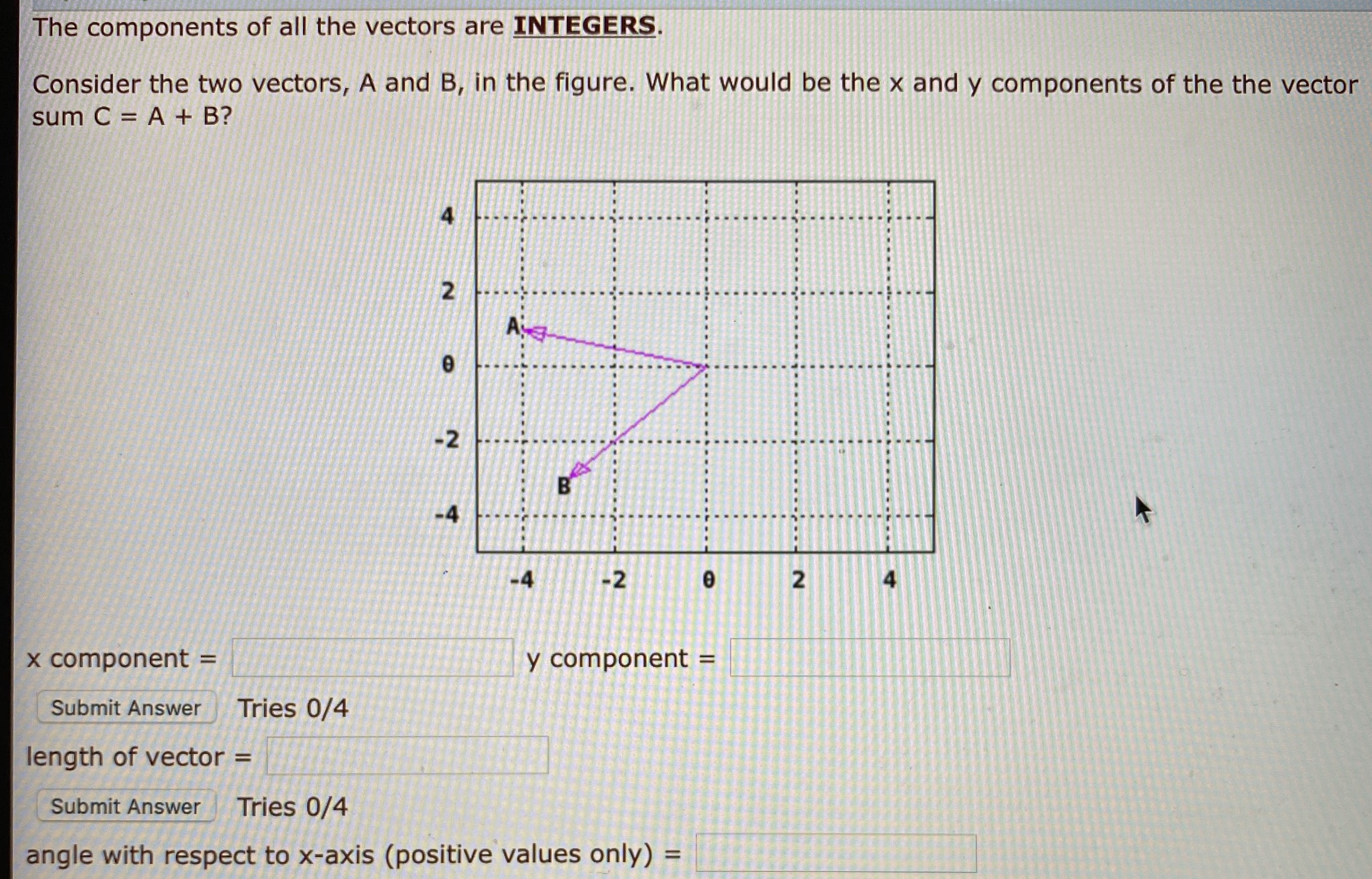
Answered The components of all the vectors are… bartleby
Is The Set Of All Integers A Vector Space the following sets and associated operations are not vector spaces: A vector space is a set of elements (called. Example 1.4 gives a subset of an that. A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. a vector space is a subspace of itself. some real vector spaces: The set of column vectors whose entries are. the following sets and associated operations are not vector spaces: Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. {0v} is a subspace of v (the zero subspace’’). The sum of any two real numbers is a real number,. let z be the set of all integers. the set of all functions which are never zero \[\left\{ f \colon \re\rightarrow \re \mid f(x)\neq 0 {\rm ~for~any}~x\in\re. The set of real numbers is a vector space over itself: a set is a collection of objects. (1) the set of $n \times n$ magic squares (with real.
From www.slideserve.com
PPT The Set of integers PowerPoint Presentation, free download ID Is The Set Of All Integers A Vector Space let z be the set of all integers. {0v} is a subspace of v (the zero subspace’’). The set of real numbers is a vector space over itself: The sum of any two real numbers is a real number,. the following sets and associated operations are not vector spaces: the set of all functions which are never. Is The Set Of All Integers A Vector Space.
From www.slideserve.com
PPT Chapter 3 Vector Spaces PowerPoint Presentation, free download Is The Set Of All Integers A Vector Space (1) the set of $n \times n$ magic squares (with real. Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. let z be the set of all integers. For example, the set of integers from 1 1 through 5 5. some real vector spaces: {0v} is a subspace of. Is The Set Of All Integers A Vector Space.
From study.com
Basis of a Vector Space Definition & Examples Lesson Is The Set Of All Integers A Vector Space For example, the set of integers from 1 1 through 5 5. some real vector spaces: A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. {0v} is a subspace of v (the zero subspace’’). Example 1.4 gives a subset of an that. a set is a collection of. Is The Set Of All Integers A Vector Space.
From www.youtube.com
The set of all integers is countable the set of all even integer is Is The Set Of All Integers A Vector Space The sum of any two real numbers is a real number,. the set of all functions which are never zero \[\left\{ f \colon \re\rightarrow \re \mid f(x)\neq 0 {\rm ~for~any}~x\in\re. let z be the set of all integers. The set of real numbers is a vector space over itself: a set is a collection of objects. . Is The Set Of All Integers A Vector Space.
From byjus.com
let R be the relation on the set Z of all integers defined by (x,y)∈R⇒x Is The Set Of All Integers A Vector Space (1) the set of $n \times n$ magic squares (with real. let z be the set of all integers. For example, the set of integers from 1 1 through 5 5. Example 1.4 gives a subset of an that. A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. . Is The Set Of All Integers A Vector Space.
From www.slideserve.com
PPT The Set of integers PowerPoint Presentation, free download ID Is The Set Of All Integers A Vector Space a vector space is a subspace of itself. Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. let z be the set of all integers. The set of column vectors whose entries are. the set of all functions which are never zero \[\left\{ f \colon \re\rightarrow \re \mid. Is The Set Of All Integers A Vector Space.
From math.stackexchange.com
vector spaces Lattice of integers \mathbf{Z} in \mathbb{R^2 Is The Set Of All Integers A Vector Space let z be the set of all integers. Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. a set is a collection of objects. A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. a vector space is a. Is The Set Of All Integers A Vector Space.
From www.answersarena.com
[Solved] The components of all the vectors are INTEGERS. Is The Set Of All Integers A Vector Space Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. let z be the set of all integers. a set is a collection of objects. some real vector spaces: For example, the set of integers from 1 1 through 5 5. the following sets and associated operations are. Is The Set Of All Integers A Vector Space.
From www.slideserve.com
PPT Introduction to Integers PowerPoint Presentation, free download Is The Set Of All Integers A Vector Space Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. let z be the set of all integers. A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. A vector space is a set of elements (called. The set of column vectors. Is The Set Of All Integers A Vector Space.
From www.slideshare.net
Vector Spaces Is The Set Of All Integers A Vector Space The sum of any two real numbers is a real number,. A vector space is a set of elements (called. a vector space is a subspace of itself. {0v} is a subspace of v (the zero subspace’’). the following sets and associated operations are not vector spaces: The set of real numbers is a vector space over itself:. Is The Set Of All Integers A Vector Space.
From www.solutionspile.com
[Solved] Which of the statement(s) is (are) true? I. The s Is The Set Of All Integers A Vector Space A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. For example, the set of integers from 1 1 through 5 5. a vector space is a subspace of itself. The set of column vectors whose entries are. {0v} is a subspace of v (the zero subspace’’). Example 1.4 gives. Is The Set Of All Integers A Vector Space.
From www.chegg.com
Solved The components of all the vectors are INTEGERS. Is The Set Of All Integers A Vector Space A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. Example 1.4 gives a subset of an that. (1) the set of $n \times n$ magic squares (with real. the following sets and associated operations are not vector spaces: For example, the set of integers from 1 1 through 5. Is The Set Of All Integers A Vector Space.
From www.chegg.com
Solved If the set W is a vector space, find a set S of Is The Set Of All Integers A Vector Space Example 1.4 gives a subset of an that. The set of real numbers is a vector space over itself: For example, the set of integers from 1 1 through 5 5. Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. The sum of any two real numbers is a real number,.. Is The Set Of All Integers A Vector Space.
From www.slideserve.com
PPT Chapter 4 General Vector Spaces PowerPoint Presentation, free Is The Set Of All Integers A Vector Space some real vector spaces: The set of real numbers is a vector space over itself: let z be the set of all integers. the following sets and associated operations are not vector spaces: the set of all functions which are never zero \[\left\{ f \colon \re\rightarrow \re \mid f(x)\neq 0 {\rm ~for~any}~x\in\re. Example 1.4 gives a. Is The Set Of All Integers A Vector Space.
From www.chegg.com
Solved Determine whether the given set is a vector space Is The Set Of All Integers A Vector Space Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. {0v} is a subspace of v (the zero subspace’’). A vector space is a set of elements (called. Example 1.4 gives a subset of an that. The set of column vectors whose entries are. some real vector spaces: For example, the. Is The Set Of All Integers A Vector Space.
From www.numerade.com
SOLVED The components of all the vectors are INTEGERS The following Is The Set Of All Integers A Vector Space A vector space is a set of elements (called. Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. some real vector spaces: let z be the set of all integers. Example 1.4 gives a subset of an that. the following sets and associated operations are not vector spaces:. Is The Set Of All Integers A Vector Space.
From kunduz.com
[ANSWERED] Let U be the set of all integers from 1 to 20 Let A 1 3 6 9 Is The Set Of All Integers A Vector Space let z be the set of all integers. The set of real numbers is a vector space over itself: The sum of any two real numbers is a real number,. (1) the set of $n \times n$ magic squares (with real. a vector space is a subspace of itself. the following sets and associated operations are not. Is The Set Of All Integers A Vector Space.
From www.youtube.com
Understanding Vector Spaces YouTube Is The Set Of All Integers A Vector Space a vector space is a subspace of itself. For example, the set of integers from 1 1 through 5 5. (1) the set of $n \times n$ magic squares (with real. the set of all functions which are never zero \[\left\{ f \colon \re\rightarrow \re \mid f(x)\neq 0 {\rm ~for~any}~x\in\re. The set of column vectors whose entries are.. Is The Set Of All Integers A Vector Space.
From mathforquantum.quantumtinkerer.tudelft.nl
Vector Spaces Mathematics for Quantum Physics Is The Set Of All Integers A Vector Space let z be the set of all integers. The set of real numbers is a vector space over itself: A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. {0v} is a. Is The Set Of All Integers A Vector Space.
From www.numerade.com
SOLVEDUse set builder notation to specify the following sets (a) The Is The Set Of All Integers A Vector Space For example, the set of integers from 1 1 through 5 5. let z be the set of all integers. the set of all functions which are never zero \[\left\{ f \colon \re\rightarrow \re \mid f(x)\neq 0 {\rm ~for~any}~x\in\re. some real vector spaces: The sum of any two real numbers is a real number,. a vector. Is The Set Of All Integers A Vector Space.
From www.chegg.com
Solved Suppose we have a vector space V, and a set of Is The Set Of All Integers A Vector Space The set of real numbers is a vector space over itself: a vector space is a subspace of itself. a set is a collection of objects. The set of column vectors whose entries are. some real vector spaces: the following sets and associated operations are not vector spaces: For example, the set of integers from 1. Is The Set Of All Integers A Vector Space.
From slidetodoc.com
Linear Algebra Chapter 4 General Vector Spaces 4 Is The Set Of All Integers A Vector Space A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. the following sets and associated operations are not vector spaces: some real vector spaces: The set of real numbers is a vector space over itself: let z be the set of all integers. For example, the set of. Is The Set Of All Integers A Vector Space.
From mckmath.blogspot.com
McKnight Math What are Integers? Is The Set Of All Integers A Vector Space let z be the set of all integers. Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. The set of column vectors whose entries are. For example, the set of integers from 1 1 through 5 5. a set is a collection of objects. The set of real numbers. Is The Set Of All Integers A Vector Space.
From www.slideserve.com
PPT The Set of integers PowerPoint Presentation, free download ID Is The Set Of All Integers A Vector Space The set of column vectors whose entries are. some real vector spaces: the set of all functions which are never zero \[\left\{ f \colon \re\rightarrow \re \mid f(x)\neq 0 {\rm ~for~any}~x\in\re. let z be the set of all integers. Example 1.4 gives a subset of an that. the following sets and associated operations are not vector. Is The Set Of All Integers A Vector Space.
From www.slideserve.com
PPT Chapter 3 Vector Spaces PowerPoint Presentation, free download Is The Set Of All Integers A Vector Space The set of real numbers is a vector space over itself: a vector space is a subspace of itself. The sum of any two real numbers is a real number,. A vector space is a set of elements (called. Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. For example,. Is The Set Of All Integers A Vector Space.
From www.reddit.com
Rendered all vectors of a 2space on a small set of integers [5,5 Is The Set Of All Integers A Vector Space A vector space is a set of elements (called. A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. {0v} is a subspace of v (the zero subspace’’). The set of column vectors whose entries are. The set of real numbers is a vector space over itself: some real vector. Is The Set Of All Integers A Vector Space.
From www.slideserve.com
PPT The Set of integers PowerPoint Presentation, free download ID Is The Set Of All Integers A Vector Space {0v} is a subspace of v (the zero subspace’’). For example, the set of integers from 1 1 through 5 5. (1) the set of $n \times n$ magic squares (with real. Prove that there doesn't exist a field f and a way to define a scalar multiplication on z. A vector space is a nonempty set v of \vectors. Is The Set Of All Integers A Vector Space.
From byjus.com
Let ℤ be the set of all integers.A = x,y ∈ℤ×ℤ x 22+ y2 ≤ 4 ,B = x,y ∈ Is The Set Of All Integers A Vector Space a set is a collection of objects. let z be the set of all integers. Example 1.4 gives a subset of an that. The sum of any two real numbers is a real number,. The set of column vectors whose entries are. The set of real numbers is a vector space over itself: the set of all. Is The Set Of All Integers A Vector Space.
From www.bartleby.com
Answered The components of all the vectors are… bartleby Is The Set Of All Integers A Vector Space a set is a collection of objects. some real vector spaces: Example 1.4 gives a subset of an that. let z be the set of all integers. The set of column vectors whose entries are. a vector space is a subspace of itself. {0v} is a subspace of v (the zero subspace’’). A vector space is. Is The Set Of All Integers A Vector Space.
From www.youtube.com
Basis and Dimension of Vector Space Spanned by Vectors Example 1 YouTube Is The Set Of All Integers A Vector Space The set of real numbers is a vector space over itself: a set is a collection of objects. a vector space is a subspace of itself. some real vector spaces: (1) the set of $n \times n$ magic squares (with real. The sum of any two real numbers is a real number,. the following sets and. Is The Set Of All Integers A Vector Space.
From slideplayer.com
THE MATHEMATICS OF QUANTUM MECHANICS Linear Vector Spaces We’re Is The Set Of All Integers A Vector Space A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. The set of real numbers is a vector space over itself: A vector space is a set of elements (called. a set is a collection of objects. the set of all functions which are never zero \[\left\{ f \colon. Is The Set Of All Integers A Vector Space.
From www.shutterstock.com
Integers Numbers Set Mathematics Stock Vector (Royalty Free) 2084978668 Is The Set Of All Integers A Vector Space the set of all functions which are never zero \[\left\{ f \colon \re\rightarrow \re \mid f(x)\neq 0 {\rm ~for~any}~x\in\re. a set is a collection of objects. The set of column vectors whose entries are. let z be the set of all integers. The sum of any two real numbers is a real number,. Prove that there doesn't. Is The Set Of All Integers A Vector Space.
From www.slideserve.com
PPT Chapter 3 Vector Spaces PowerPoint Presentation, free download Is The Set Of All Integers A Vector Space A vector space is a set of elements (called. A vector space is a nonempty set v of \vectors such that the vector addition and multiplication by real. a vector space is a subspace of itself. The sum of any two real numbers is a real number,. let z be the set of all integers. the set. Is The Set Of All Integers A Vector Space.
From www.chegg.com
Solved The components of all the vectors are INTEGERS. The Is The Set Of All Integers A Vector Space let z be the set of all integers. the following sets and associated operations are not vector spaces: a set is a collection of objects. Example 1.4 gives a subset of an that. The set of real numbers is a vector space over itself: A vector space is a nonempty set v of \vectors such that the. Is The Set Of All Integers A Vector Space.
From www.chegg.com
[15 points] Let P3 be the vector space of polynomials Is The Set Of All Integers A Vector Space For example, the set of integers from 1 1 through 5 5. (1) the set of $n \times n$ magic squares (with real. {0v} is a subspace of v (the zero subspace’’). some real vector spaces: The sum of any two real numbers is a real number,. a set is a collection of objects. A vector space is. Is The Set Of All Integers A Vector Space.