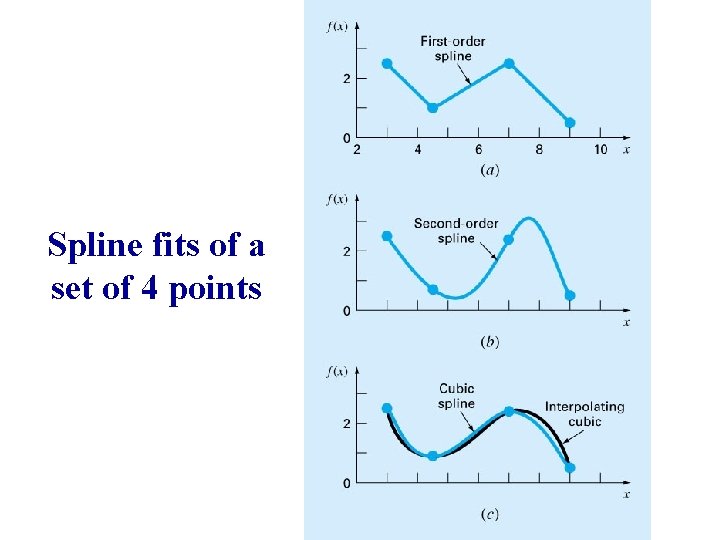
What Are Splines Used For In Statistics . the point of separation in the piecewise regression system is called a knot. For linear splines, there are two things to consider: over and underfitting are common problems when using splines. They are piecewise polynomials of order k (k=3. splines can fit complex functions with few parameters. the set of functions we use define the basis of a vector space. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). F k t1 < < tr k. Polynomials require high degree terms to be flexible. We can select the knot a priori (say, at the. We can have more than one knot. Of degree with knots at that is continuous and has continuous derivatives of orders 1;
from slidetodoc.com
over and underfitting are common problems when using splines. the set of functions we use define the basis of a vector space. the point of separation in the piecewise regression system is called a knot. They are piecewise polynomials of order k (k=3. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). Of degree with knots at that is continuous and has continuous derivatives of orders 1; Polynomials require high degree terms to be flexible. For linear splines, there are two things to consider: F k t1 < < tr k. We can select the knot a priori (say, at the.
Chapter 16 Curve Fitting Splines Spline Interpolation z
What Are Splines Used For In Statistics We can select the knot a priori (say, at the. Polynomials require high degree terms to be flexible. We can have more than one knot. the point of separation in the piecewise regression system is called a knot. They are piecewise polynomials of order k (k=3. splines can fit complex functions with few parameters. Of degree with knots at that is continuous and has continuous derivatives of orders 1; For linear splines, there are two things to consider: In polynomial regression the basis functions are \(1, x, x^2,., x^d\). We can select the knot a priori (say, at the. F k t1 < < tr k. over and underfitting are common problems when using splines. the set of functions we use define the basis of a vector space.
From datascienceplus.com
Cubic and Smoothing Splines in R DataScience+ What Are Splines Used For In Statistics We can select the knot a priori (say, at the. Of degree with knots at that is continuous and has continuous derivatives of orders 1; the point of separation in the piecewise regression system is called a knot. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). F k t1 < < tr k. We can have. What Are Splines Used For In Statistics.
From datavizproject.com
Spline Graph Data Viz Project What Are Splines Used For In Statistics the set of functions we use define the basis of a vector space. Of degree with knots at that is continuous and has continuous derivatives of orders 1; splines can fit complex functions with few parameters. the point of separation in the piecewise regression system is called a knot. We can have more than one knot. For. What Are Splines Used For In Statistics.
From www.researchgate.net
1 The first three bsplines used in spatial shape function 1 What Are Splines Used For In Statistics In polynomial regression the basis functions are \(1, x, x^2,., x^d\). over and underfitting are common problems when using splines. the point of separation in the piecewise regression system is called a knot. F k t1 < < tr k. We can have more than one knot. For linear splines, there are two things to consider: Polynomials require. What Are Splines Used For In Statistics.
From slidetodoc.com
Chapter 16 Curve Fitting Splines Spline Interpolation z What Are Splines Used For In Statistics splines can fit complex functions with few parameters. F k t1 < < tr k. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). over and underfitting are common problems when using splines. They are piecewise polynomials of order k (k=3. We can select the knot a priori (say, at the. Of degree with knots at. What Are Splines Used For In Statistics.
From www.youtube.com
Introduction to Splines YouTube What Are Splines Used For In Statistics the point of separation in the piecewise regression system is called a knot. For linear splines, there are two things to consider: over and underfitting are common problems when using splines. Polynomials require high degree terms to be flexible. We can select the knot a priori (say, at the. splines can fit complex functions with few parameters.. What Are Splines Used For In Statistics.
From www.slideshare.net
Spline Interpolation What Are Splines Used For In Statistics For linear splines, there are two things to consider: Of degree with knots at that is continuous and has continuous derivatives of orders 1; We can have more than one knot. over and underfitting are common problems when using splines. the point of separation in the piecewise regression system is called a knot. Polynomials require high degree terms. What Are Splines Used For In Statistics.
From slidetodoc.com
Chapter 16 Curve Fitting Splines Spline Interpolation z What Are Splines Used For In Statistics We can select the knot a priori (say, at the. the set of functions we use define the basis of a vector space. F k t1 < < tr k. Polynomials require high degree terms to be flexible. splines can fit complex functions with few parameters. Of degree with knots at that is continuous and has continuous derivatives. What Are Splines Used For In Statistics.
From root.cern
ROOT tutorials/graphs/splines_test.C File Reference What Are Splines Used For In Statistics We can have more than one knot. Polynomials require high degree terms to be flexible. the set of functions we use define the basis of a vector space. the point of separation in the piecewise regression system is called a knot. They are piecewise polynomials of order k (k=3. F k t1 < < tr k. Of degree. What Are Splines Used For In Statistics.
From bcheggeseth.github.io
Topic 9 Splines STAT 253 Statistical Machine Learning What Are Splines Used For In Statistics For linear splines, there are two things to consider: F k t1 < < tr k. Polynomials require high degree terms to be flexible. We can have more than one knot. Of degree with knots at that is continuous and has continuous derivatives of orders 1; In polynomial regression the basis functions are \(1, x, x^2,., x^d\). over and. What Are Splines Used For In Statistics.
From slidetodoc.com
Chapter 16 Curve Fitting Splines Spline Interpolation z What Are Splines Used For In Statistics F k t1 < < tr k. They are piecewise polynomials of order k (k=3. We can have more than one knot. We can select the knot a priori (say, at the. the set of functions we use define the basis of a vector space. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). over and. What Are Splines Used For In Statistics.
From patsy.readthedocs.io
Spline regression — patsy 0.5.1+dev documentation What Are Splines Used For In Statistics the set of functions we use define the basis of a vector space. the point of separation in the piecewise regression system is called a knot. Of degree with knots at that is continuous and has continuous derivatives of orders 1; F k t1 < < tr k. We can select the knot a priori (say, at the.. What Are Splines Used For In Statistics.
From www.slideshare.net
Spline Interpolation What Are Splines Used For In Statistics For linear splines, there are two things to consider: the point of separation in the piecewise regression system is called a knot. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). F k t1 < < tr k. Of degree with knots at that is continuous and has continuous derivatives of orders 1; We can have more. What Are Splines Used For In Statistics.
From slidetodoc.com
Chapter 16 Curve Fitting Splines Spline Interpolation z What Are Splines Used For In Statistics They are piecewise polynomials of order k (k=3. splines can fit complex functions with few parameters. over and underfitting are common problems when using splines. We can select the knot a priori (say, at the. F k t1 < < tr k. Of degree with knots at that is continuous and has continuous derivatives of orders 1; We. What Are Splines Used For In Statistics.
From saslist.com
Three ways to add a smoothing spline to a scatter plot in SAS » SAS博客列表 What Are Splines Used For In Statistics splines can fit complex functions with few parameters. For linear splines, there are two things to consider: Polynomials require high degree terms to be flexible. the set of functions we use define the basis of a vector space. Of degree with knots at that is continuous and has continuous derivatives of orders 1; They are piecewise polynomials of. What Are Splines Used For In Statistics.
From www.researchgate.net
Piecewise Quadratic Splines with Multiple Knots Download Scientific What Are Splines Used For In Statistics over and underfitting are common problems when using splines. For linear splines, there are two things to consider: We can have more than one knot. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). We can select the knot a priori (say, at the. They are piecewise polynomials of order k (k=3. the point of separation. What Are Splines Used For In Statistics.
From www.researchgate.net
The Sshape fiveaxis spline toolpath used for comparison tests What Are Splines Used For In Statistics F k t1 < < tr k. Of degree with knots at that is continuous and has continuous derivatives of orders 1; In polynomial regression the basis functions are \(1, x, x^2,., x^d\). We can have more than one knot. the set of functions we use define the basis of a vector space. Polynomials require high degree terms to. What Are Splines Used For In Statistics.
From teazrq.github.io
Chapter 9 Spline Statistical Learning and Machine Learning with R What Are Splines Used For In Statistics the set of functions we use define the basis of a vector space. We can select the knot a priori (say, at the. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). Polynomials require high degree terms to be flexible. over and underfitting are common problems when using splines. They are piecewise polynomials of order k. What Are Splines Used For In Statistics.
From www.researchgate.net
Nonuniform rational Bsplines curve Download Scientific Diagram What Are Splines Used For In Statistics Of degree with knots at that is continuous and has continuous derivatives of orders 1; For linear splines, there are two things to consider: over and underfitting are common problems when using splines. splines can fit complex functions with few parameters. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). They are piecewise polynomials of order. What Are Splines Used For In Statistics.
From www.researchgate.net
8 Comparing Smoothing splines (Ssplines), hybrid splines (Hsplines What Are Splines Used For In Statistics In polynomial regression the basis functions are \(1, x, x^2,., x^d\). Polynomials require high degree terms to be flexible. We can have more than one knot. We can select the knot a priori (say, at the. For linear splines, there are two things to consider: over and underfitting are common problems when using splines. Of degree with knots at. What Are Splines Used For In Statistics.
From www.slideserve.com
PPT Image Content Representation PowerPoint Presentation, free What Are Splines Used For In Statistics the set of functions we use define the basis of a vector space. We can have more than one knot. For linear splines, there are two things to consider: They are piecewise polynomials of order k (k=3. Of degree with knots at that is continuous and has continuous derivatives of orders 1; In polynomial regression the basis functions are. What Are Splines Used For In Statistics.
From asbates.rbind.io
Splines What Are They? Some Clever Stats Name What Are Splines Used For In Statistics F k t1 < < tr k. For linear splines, there are two things to consider: We can select the knot a priori (say, at the. the set of functions we use define the basis of a vector space. We can have more than one knot. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). They are. What Are Splines Used For In Statistics.
From bookdown.org
Chapter 9 Splines Machine Learning What Are Splines Used For In Statistics splines can fit complex functions with few parameters. the point of separation in the piecewise regression system is called a knot. Polynomials require high degree terms to be flexible. We can select the knot a priori (say, at the. They are piecewise polynomials of order k (k=3. F k t1 < < tr k. For linear splines, there. What Are Splines Used For In Statistics.
From www.researchgate.net
Top a cubic Bspline curve in 3D space with eight control points What Are Splines Used For In Statistics For linear splines, there are two things to consider: They are piecewise polynomials of order k (k=3. Of degree with knots at that is continuous and has continuous derivatives of orders 1; F k t1 < < tr k. over and underfitting are common problems when using splines. We can have more than one knot. We can select the. What Are Splines Used For In Statistics.
From slidetodoc.com
Chapter 16 Curve Fitting Splines Spline Interpolation z What Are Splines Used For In Statistics over and underfitting are common problems when using splines. Polynomials require high degree terms to be flexible. splines can fit complex functions with few parameters. Of degree with knots at that is continuous and has continuous derivatives of orders 1; the set of functions we use define the basis of a vector space. In polynomial regression the. What Are Splines Used For In Statistics.
From opensourc.es
Bsplines What Are Splines Used For In Statistics splines can fit complex functions with few parameters. the point of separation in the piecewise regression system is called a knot. over and underfitting are common problems when using splines. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). For linear splines, there are two things to consider: They are piecewise polynomials of order k. What Are Splines Used For In Statistics.
From opensourc.es
Bsplines What Are Splines Used For In Statistics We can have more than one knot. F k t1 < < tr k. They are piecewise polynomials of order k (k=3. the point of separation in the piecewise regression system is called a knot. over and underfitting are common problems when using splines. splines can fit complex functions with few parameters. In polynomial regression the basis. What Are Splines Used For In Statistics.
From psu.pb.unizin.org
Chapter Three Quadratic Spline Interpolation The Art of Polynomial What Are Splines Used For In Statistics splines can fit complex functions with few parameters. Of degree with knots at that is continuous and has continuous derivatives of orders 1; over and underfitting are common problems when using splines. We can have more than one knot. the set of functions we use define the basis of a vector space. We can select the knot. What Are Splines Used For In Statistics.
From www.slideserve.com
PPT Splines PowerPoint Presentation, free download ID733508 What Are Splines Used For In Statistics over and underfitting are common problems when using splines. F k t1 < < tr k. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). We can have more than one knot. Polynomials require high degree terms to be flexible. the set of functions we use define the basis of a vector space. Of degree with. What Are Splines Used For In Statistics.
From www.youtube.com
Polynomial Regression and Splines YouTube What Are Splines Used For In Statistics the point of separation in the piecewise regression system is called a knot. over and underfitting are common problems when using splines. F k t1 < < tr k. We can select the knot a priori (say, at the. the set of functions we use define the basis of a vector space. For linear splines, there are. What Are Splines Used For In Statistics.
From bradleyboehmke.github.io
Chapter 7 Multivariate Adaptive Regression Splines HandsOn Machine What Are Splines Used For In Statistics We can select the knot a priori (say, at the. over and underfitting are common problems when using splines. F k t1 < < tr k. For linear splines, there are two things to consider: Polynomials require high degree terms to be flexible. the set of functions we use define the basis of a vector space. splines. What Are Splines Used For In Statistics.
From slidetodoc.com
Chapter 16 Curve Fitting Splines Spline Interpolation z What Are Splines Used For In Statistics Of degree with knots at that is continuous and has continuous derivatives of orders 1; splines can fit complex functions with few parameters. Polynomials require high degree terms to be flexible. They are piecewise polynomials of order k (k=3. We can select the knot a priori (say, at the. the point of separation in the piecewise regression system. What Are Splines Used For In Statistics.
From www.youtube.com
smoothing splines in R degrees of freedom in smooth.spline data What Are Splines Used For In Statistics For linear splines, there are two things to consider: We can have more than one knot. F k t1 < < tr k. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). splines can fit complex functions with few parameters. They are piecewise polynomials of order k (k=3. the set of functions we use define the. What Are Splines Used For In Statistics.
From www.slideserve.com
PPT Polynomial PowerPoint Presentation, free download ID688839 What Are Splines Used For In Statistics We can select the knot a priori (say, at the. over and underfitting are common problems when using splines. For linear splines, there are two things to consider: the point of separation in the piecewise regression system is called a knot. the set of functions we use define the basis of a vector space. We can have. What Are Splines Used For In Statistics.
From slidetodoc.com
Chapter 16 Curve Fitting Splines Spline Interpolation z What Are Splines Used For In Statistics F k t1 < < tr k. They are piecewise polynomials of order k (k=3. the point of separation in the piecewise regression system is called a knot. over and underfitting are common problems when using splines. the set of functions we use define the basis of a vector space. We can select the knot a priori. What Are Splines Used For In Statistics.
From link.springer.com
Compositional splines for representation of density functions What Are Splines Used For In Statistics Polynomials require high degree terms to be flexible. We can have more than one knot. For linear splines, there are two things to consider: splines can fit complex functions with few parameters. the point of separation in the piecewise regression system is called a knot. In polynomial regression the basis functions are \(1, x, x^2,., x^d\). They are. What Are Splines Used For In Statistics.