Cylindrical Jacobian . for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. changing variables in triple integrals works in exactly the same way. Cylindrical and spherical coordinate substitutions are special. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The jacobian of cylindrical coordinates. this determinant is called the jacobian of the transformation of coordinates. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical.
from www.chegg.com
Cylindrical and spherical coordinate substitutions are special. changing variables in triple integrals works in exactly the same way. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. The jacobian of cylindrical coordinates. this determinant is called the jacobian of the transformation of coordinates. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand.
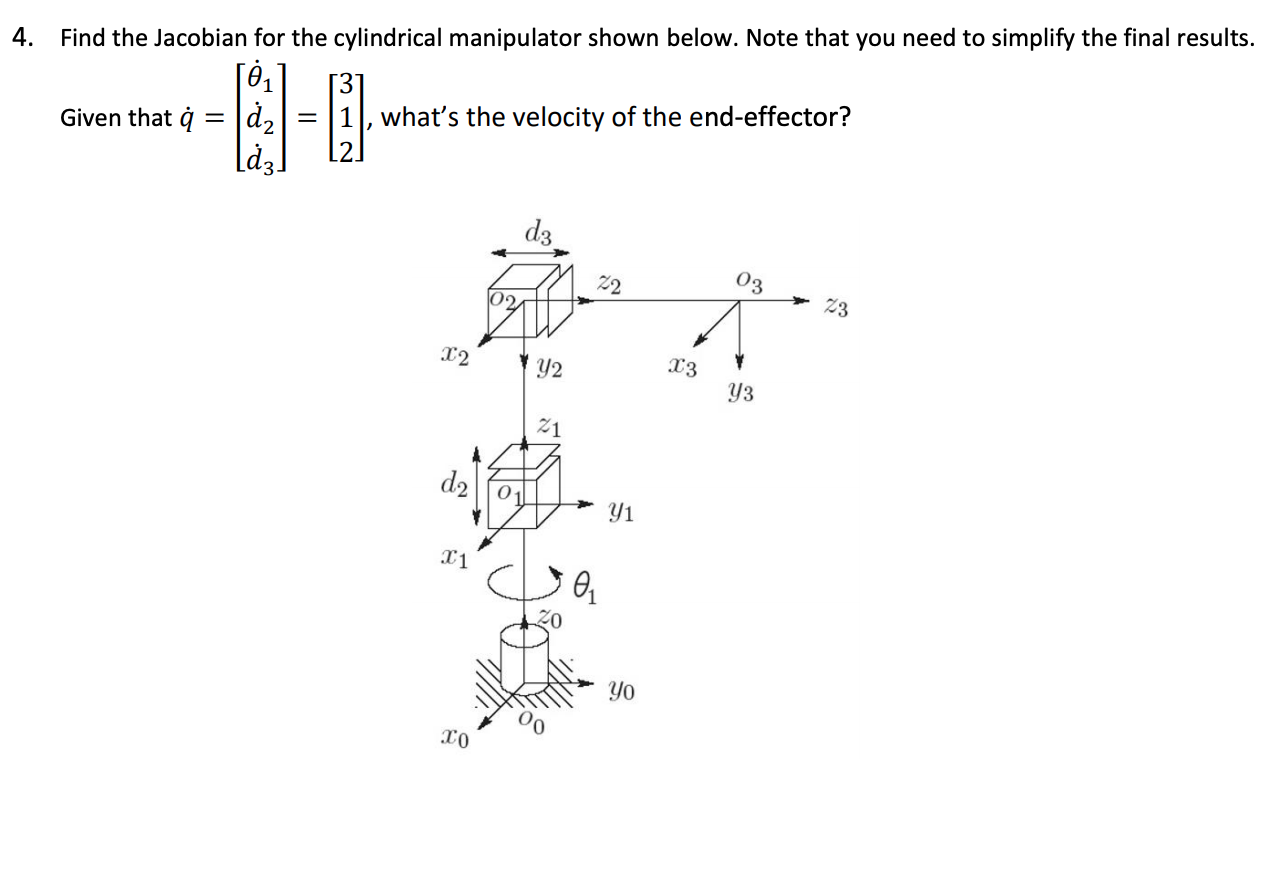
Solved 4. Find the Jacobian for the cylindrical manipulator
Cylindrical Jacobian Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. Cylindrical and spherical coordinate substitutions are special. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. changing variables in triple integrals works in exactly the same way. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. this determinant is called the jacobian of the transformation of coordinates. The jacobian of cylindrical coordinates.
From www.chegg.com
Solved 4. Find the Jacobian for the cylindrical manipulator Cylindrical Jacobian cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. this determinant is called the jacobian of the transformation of coordinates. for example this is how one changes an. Cylindrical Jacobian.
From www.youtube.com
Cylindrical Manipulator Full Example HTM and Jacobian Matrix YouTube Cylindrical Jacobian for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. this determinant is called the jacobian of the transformation of coordinates. Cylindrical and spherical coordinate substitutions are special. The jacobian of cylindrical coordinates. changing variables in triple integrals works in exactly the same way. Just as we did with polar. Cylindrical Jacobian.
From www.chegg.com
Find the Jacobian for the threelink cylindrical Cylindrical Jacobian The jacobian of cylindrical coordinates. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. this determinant is called the jacobian of the transformation of coordinates. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. cylindrical and spherical coordinates give. Cylindrical Jacobian.
From www.slideserve.com
PPT Velocity Analysis Jacobian PowerPoint Presentation, free download Cylindrical Jacobian The jacobian of cylindrical coordinates. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. Cylindrical and spherical coordinate substitutions are special. this determinant is called the jacobian of the. Cylindrical Jacobian.
From math.stackexchange.com
multivariable calculus Computing the Jacobian for the change of Cylindrical Jacobian for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. Cylindrical and spherical coordinate substitutions are special. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to. Cylindrical Jacobian.
From phoevoseneko.blogspot.com
20+ calculator jacobian PhoevosEneko Cylindrical Jacobian The jacobian of cylindrical coordinates. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. changing variables in triple integrals works in exactly the same way. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. Just as we did. Cylindrical Jacobian.
From community.freefem.org
Cylindrical Coordinates and the jacobian General Discussion FreeFEM Cylindrical Jacobian this determinant is called the jacobian of the transformation of coordinates. changing variables in triple integrals works in exactly the same way. Cylindrical and spherical coordinate substitutions are special. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. for example this is how one changes an. Cylindrical Jacobian.
From www.chegg.com
Solved Problem 3 (20pts) Calculate the Jacobian matrix and Cylindrical Jacobian The jacobian of cylindrical coordinates. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. Cylindrical and spherical coordinate substitutions are special. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. for example this is how one changes an. Cylindrical Jacobian.
From www.youtube.com
L2 Coordinate Transformation and Jacobian YouTube Cylindrical Jacobian The jacobian of cylindrical coordinates. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. Cylindrical and spherical coordinate substitutions are special. this determinant is called the jacobian of the transformation of coordinates. changing variables in triple integrals works in exactly the same way. Just as we did with. Cylindrical Jacobian.
From www.coursehero.com
[Solved] Find the Jacobian for a cylindrical system. Course Hero Cylindrical Jacobian for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. this determinant is called the jacobian of the transformation of coordinates. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. The jacobian of cylindrical coordinates. Cylindrical and spherical coordinate substitutions are. Cylindrical Jacobian.
From math.stackexchange.com
jacobian Converting integral to cylindrical coordinates Mathematics Cylindrical Jacobian after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. this determinant is called the jacobian of the transformation of coordinates. changing variables in triple integrals works in exactly. Cylindrical Jacobian.
From www.slideserve.com
PPT Chapter 15 Multiple Integrals PowerPoint Presentation, free Cylindrical Jacobian Cylindrical and spherical coordinate substitutions are special. The jacobian of cylindrical coordinates. this determinant is called the jacobian of the transformation of coordinates. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions. Cylindrical Jacobian.
From www.chegg.com
Find the Jacobian for the threelink cylindrical Cylindrical Jacobian cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. this determinant is called the jacobian of the transformation of coordinates. The jacobian of cylindrical coordinates. Cylindrical and spherical coordinate substitutions are special. for example this is how one changes an integral in rectangular coordinates to cylindrical or. Cylindrical Jacobian.
From www.studypool.com
SOLUTION Vector calculus change of variables jacobian transformation Cylindrical Jacobian The jacobian of cylindrical coordinates. Cylindrical and spherical coordinate substitutions are special. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. this determinant is called the jacobian of the transformation of coordinates. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical. Cylindrical Jacobian.
From www.youtube.com
Cylindrical polar coordinates 🙄 Problem based on Jacobian Cylindrical Jacobian for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. this determinant is called the jacobian of the transformation of coordinates. The jacobian of cylindrical coordinates. changing variables in triple. Cylindrical Jacobian.
From www.kristakingmath.com
Jacobian in three variables to change variables — Krista King Math Cylindrical Jacobian for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. Cylindrical and spherical coordinate substitutions are special. changing variables in triple integrals works in exactly the same way. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. this determinant. Cylindrical Jacobian.
From respuestas.me
¿Por qué tienes que incluir el jacobiano para cada sistema de Cylindrical Jacobian for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The jacobian of. Cylindrical Jacobian.
From math.stackexchange.com
jacobian Converting integral to cylindrical coordinates Mathematics Cylindrical Jacobian for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. The jacobian of. Cylindrical Jacobian.
From www.chegg.com
Solved Consider the formulation of a triple integral in Cylindrical Jacobian changing variables in triple integrals works in exactly the same way. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. Just as we did with polar coordinates in two dimensions,. Cylindrical Jacobian.
From www.researchgate.net
(PDF) Shape‐preserving finite elements in cylindrical and spherical Cylindrical Jacobian Cylindrical and spherical coordinate substitutions are special. changing variables in triple integrals works in exactly the same way. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. Just as we. Cylindrical Jacobian.
From www.youtube.com
The Jacobian and coordinate transformations Calculus in a Nutshell Cylindrical Jacobian Cylindrical and spherical coordinate substitutions are special. this determinant is called the jacobian of the transformation of coordinates. changing variables in triple integrals works in exactly the same way. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. The jacobian of cylindrical coordinates. for example this is. Cylindrical Jacobian.
From math.stackexchange.com
jacobian Converting integral to cylindrical coordinates Mathematics Cylindrical Jacobian cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. changing variables. Cylindrical Jacobian.
From www.sefidian.com
Understanding Jacobian and Hessian matrices with example Cylindrical Jacobian Cylindrical and spherical coordinate substitutions are special. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. The jacobian of cylindrical coordinates. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. for example this is how one changes an integral. Cylindrical Jacobian.
From www.chegg.com
420 Find the 6 x 3 Jacobian for the three links of Cylindrical Jacobian changing variables in triple integrals works in exactly the same way. The jacobian of cylindrical coordinates. Cylindrical and spherical coordinate substitutions are special. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. for example this is how one changes an integral in rectangular coordinates to cylindrical or. Cylindrical Jacobian.
From math.stackexchange.com
jacobian Converting integral to cylindrical coordinates Mathematics Cylindrical Jacobian for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. this determinant is called the jacobian of the transformation of coordinates. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. Just as we did with polar coordinates in two dimensions, we. Cylindrical Jacobian.
From www.chegg.com
Solved Find the 6 x 3 Jacobian for the threelink Cylindrical Jacobian after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. Cylindrical and spherical coordinate substitutions are special. Just as we did with polar coordinates in two dimensions, we can compute a jacobian for any change of. for example this is how one changes an integral in rectangular coordinates to cylindrical. Cylindrical Jacobian.
From www.chegg.com
Solved Find the 6 x 3 Jacobian for the three links of the Cylindrical Jacobian after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. changing variables in triple integrals works in exactly the same way. Just as we did with polar coordinates in two. Cylindrical Jacobian.
From mungfali.com
Jacobian Of Spherical Coordinates Cylindrical Jacobian Cylindrical and spherical coordinate substitutions are special. changing variables in triple integrals works in exactly the same way. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. for. Cylindrical Jacobian.
From www.youtube.com
cylindrical robot forward kinematic and jacobian YouTube Cylindrical Jacobian Cylindrical and spherical coordinate substitutions are special. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. this determinant is called the jacobian of the transformation of coordinates. for. Cylindrical Jacobian.
From www.researchgate.net
Elements composing the Jacobian matrix for the coordinate... Download Cylindrical Jacobian this determinant is called the jacobian of the transformation of coordinates. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. for example this is how one changes an. Cylindrical Jacobian.
From www.slideserve.com
PPT Forward Kinematics and Jacobians PowerPoint Presentation, free Cylindrical Jacobian The jacobian of cylindrical coordinates. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem. Cylindrical Jacobian.
From www.youtube.com
Finding and Using the Jacobian Matrix and Determinant YouTube Cylindrical Jacobian cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. changing variables in triple integrals works in exactly the same way. The jacobian of cylindrical coordinates. this determinant is called. Cylindrical Jacobian.
From www.youtube.com
Multivariable calculus Jacobian (determinant) Change of variables in Cylindrical Jacobian for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. Cylindrical and spherical coordinate substitutions are special. The jacobian of cylindrical coordinates. this determinant is called the jacobian of the transformation. Cylindrical Jacobian.
From www.youtube.com
Jacobian of Cylindrical Coordinates YouTube Cylindrical Jacobian cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. changing variables in triple integrals works in exactly the same way. for example this is how one changes an integral in rectangular coordinates to cylindrical or spherical coordinates. The jacobian of cylindrical coordinates. Cylindrical and spherical coordinate substitutions. Cylindrical Jacobian.
From respuestas.me
¿Por qué tienes que incluir el jacobiano para cada sistema de Cylindrical Jacobian cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. Cylindrical and spherical coordinate substitutions are special. changing variables in triple integrals works in exactly the same way. after rectangular (aka cartesian) coordinates, the two most common an useful coordinate systems in 3 dimensions are cylindrical. Just as. Cylindrical Jacobian.