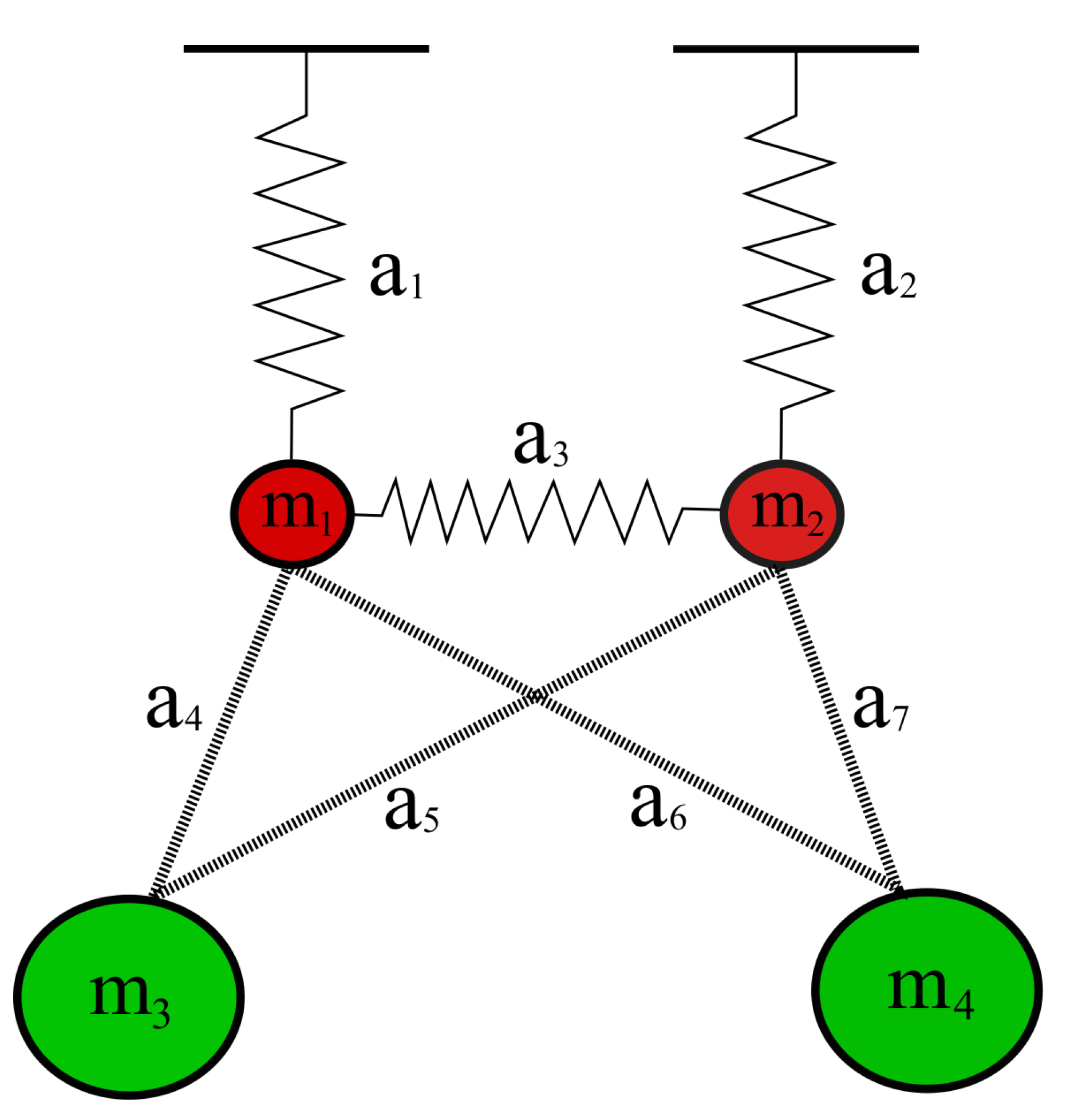
Coupled Harmonic Oscillators Hamiltonian . In addition to presenting a physically important system, this lecture, reveals a very deep connection which. We will study in depth a particular system described by the h.o., the electromagnetic field. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. Another system that can be described by this. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf.
from www.mdpi.com
A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. Another system that can be described by this. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. We will study in depth a particular system described by the h.o., the electromagnetic field. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. In addition to presenting a physically important system, this lecture, reveals a very deep connection which.
Mathematics Free FullText Coupled Harmonic Oscillator in a System
Coupled Harmonic Oscillators Hamiltonian ˆp2 2 + ax2 1 + bx2 2 + cx1x2. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. We will study in depth a particular system described by the h.o., the electromagnetic field. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. Another system that can be described by this.
From www.researchgate.net
Schematic description of a qubit coupled to a harmonic oscillator with Coupled Harmonic Oscillators Hamiltonian Another system that can be described by this. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
Solved The Hamiltonian for a simple harmonic oscillator is Coupled Harmonic Oscillators Hamiltonian A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. Another system. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
Coupled damped harmonicoscillator model showing (a) double EIT and (b Coupled Harmonic Oscillators Hamiltonian Another system that can be described by this. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. Two harmonic oscillators can be described by the. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
(a) Two coupled damped harmonic oscillators that mimic the stacked Coupled Harmonic Oscillators Hamiltonian In addition to presenting a physically important system, this lecture, reveals a very deep connection which. We will study in depth a particular system described by the h.o., the electromagnetic field. Another system that can be described by this. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf. A system of two coupled quantum harmonic oscillators with the. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
(PDF) On the geometry of conformal Hamiltonian of the timedependent Coupled Harmonic Oscillators Hamiltonian ˆp2 2 + ax2 1 + bx2 2 + cx1x2. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf. Another system that can be described by this. We will study in depth a particular system described by the h.o., the electromagnetic field. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
Solved Consider two coupled harmonic oscillators, with a Coupled Harmonic Oscillators Hamiltonian In addition to presenting a physically important system, this lecture, reveals a very deep connection which. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
Driven coupled oscillators model and finite THG above Tc a The dotted Coupled Harmonic Oscillators Hamiltonian Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. We will study in depth a particular system described by the h.o., the electromagnetic field. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. A system of two coupled quantum. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
Solved 4. The Hamiltonian of two coupled oscillators is Coupled Harmonic Oscillators Hamiltonian We will study in depth a particular system described by the h.o., the electromagnetic field. Another system that can be described by this. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
Solved (1) A system of two coupled harmonic oscillators is Coupled Harmonic Oscillators Hamiltonian ˆp2 2 + ax2 1 + bx2 2 + cx1x2. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. We will study in depth a particular system described by the h.o., the electromagnetic field. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. The. Coupled Harmonic Oscillators Hamiltonian.
From www.youtube.com
Coupled Oscillators Coordinates PTW YouTube Coupled Harmonic Oscillators Hamiltonian Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. Another system that can be described by this. In addition to presenting a. Coupled Harmonic Oscillators Hamiltonian.
From www.slideserve.com
PPT brian_Quantum information basics PowerPoint Presentation, free Coupled Harmonic Oscillators Hamiltonian Another system that can be described by this. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. We will study in depth a particular system described by. Coupled Harmonic Oscillators Hamiltonian.
From www.youtube.com
Coupled Oscillator 1 YouTube Coupled Harmonic Oscillators Hamiltonian A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. ˆp2 2. Coupled Harmonic Oscillators Hamiltonian.
From www.mdpi.com
Mathematics Free FullText Coupled Harmonic Oscillator in a System Coupled Harmonic Oscillators Hamiltonian ˆp2 2 + ax2 1 + bx2 2 + cx1x2. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. We will study in depth a particular system described by. Coupled Harmonic Oscillators Hamiltonian.
From www.slideserve.com
PPT 5. The Harmonic Oscillator PowerPoint Presentation, free download Coupled Harmonic Oscillators Hamiltonian Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. Another system that can be described by this. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf.. Coupled Harmonic Oscillators Hamiltonian.
From www.slideserve.com
PPT brian_Quantum information basics PowerPoint Presentation, free Coupled Harmonic Oscillators Hamiltonian Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. We will study in depth a particular system described by the h.o., the electromagnetic field. ˆp2 2 + ax2. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
Solved 2.2 Coupled harmonic oscillators One considers the Coupled Harmonic Oscillators Hamiltonian We will study in depth a particular system described by the h.o., the electromagnetic field. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. Another system that can be described by this. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. The coupled oscillators described this linear differential equations $$\mathbf. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
Solved Consider the 2D harmonic oscillator Hamiltonian Coupled Harmonic Oscillators Hamiltonian The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf. We will study in depth a particular system described by the h.o., the electromagnetic field. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
Solved Problem 4 Simple Harmonic Oscillator Hamiltonian Let Coupled Harmonic Oscillators Hamiltonian The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
(color online) Schematic diagram of three coupled harmonic oscillators Coupled Harmonic Oscillators Hamiltonian We will study in depth a particular system described by the h.o., the electromagnetic field. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a =. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
Solved Exercise 3 The Hamiltonian of the onedimensional Coupled Harmonic Oscillators Hamiltonian Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. Another system that can be described by this. The coupled oscillators described this. Coupled Harmonic Oscillators Hamiltonian.
From www.youtube.com
Coupled harmonic oscillator Lagrangian Classical Mechanics Coupled Harmonic Oscillators Hamiltonian Another system that can be described by this. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. We will study in depth a particular system described by the h.o., the electromagnetic field. A system of two coupled quantum harmonic oscillators with. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
Model of two coupled oscillators under two external drives Coupled Harmonic Oscillators Hamiltonian ˆp2 2 + ax2 1 + bx2 2 + cx1x2. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. Another system that can be described by this. The coupled oscillators. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
(color online) The schematic shows two coupled oscillators via a Coupled Harmonic Oscillators Hamiltonian In addition to presenting a physically important system, this lecture, reveals a very deep connection which. Another system that can be described by this. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b +. Coupled Harmonic Oscillators Hamiltonian.
From pdfprof.com
hamiltonian of coupled harmonic oscillators Coupled Harmonic Oscillators Hamiltonian Another system that can be described by this. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. We will study in depth a particular system described by the h.o., the electromagnetic field. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
Communication graph topology for coupled harmonic oscillators Coupled Harmonic Oscillators Hamiltonian A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. We will study in depth a particular system described by the h.o., the electromagnetic field. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a =. Coupled Harmonic Oscillators Hamiltonian.
From www.mdpi.com
Mathematics Free FullText Periodic Solutions and Stability Coupled Harmonic Oscillators Hamiltonian In addition to presenting a physically important system, this lecture, reveals a very deep connection which. A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. We will study in depth a particular system described by the h.o., the electromagnetic field. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf.. Coupled Harmonic Oscillators Hamiltonian.
From nanohub.org
Resources Quantum Effects in and Coupled Harmonic Oscillators Hamiltonian We will study in depth a particular system described by the h.o., the electromagnetic field. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. Another system that can be described by this. In addition to presenting a physically important system, this lecture, reveals a very deep. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
The coincidence function (38) of two coupled harmonic oscillators, one Coupled Harmonic Oscillators Hamiltonian In addition to presenting a physically important system, this lecture, reveals a very deep connection which. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. Another system that can be described by this. The coupled oscillators. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
The eigenstates of the QH Hamiltonian are harmonic oscillator states in Coupled Harmonic Oscillators Hamiltonian Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. Another system that can be described by this. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
A mechanical model of three series coupled oscillators. Download Coupled Harmonic Oscillators Hamiltonian Another system that can be described by this. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. The coupled oscillators. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
Harmonic oscillator orbits with fourthorder RungeKutta dt = 1 (blue Coupled Harmonic Oscillators Hamiltonian ˆp2 2 + ax2 1 + bx2 2 + cx1x2. Two harmonic oscillators can be described by the hamiltonian $\hat h_a + \hat h_b + \hat h_c$ where $\hat h_a = \hbar\omega(\hat a^\dagger. A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. In addition to. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
a) is the realization of the coupled oscillators (equation (2.1a) and Coupled Harmonic Oscillators Hamiltonian In addition to presenting a physically important system, this lecture, reveals a very deep connection which. The coupled oscillators described this linear differential equations $$\mathbf m\,\vec{\ddot{q}}+\mathbf k\,\vec{q}=\mathbf. We will study in depth a particular system described by the h.o., the electromagnetic field. Another system that can be described by this. ˆp2 2 + ax2 1 + bx2 2 + cx1x2.. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
Solved Two coupled harmonic oscillators The Hamilton Coupled Harmonic Oscillators Hamiltonian A system of two coupled quantum harmonic oscillators with the hamiltonian ˆh = 1 1 ˆp2 + 1. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. We will study in depth a particular system described by the h.o., the electromagnetic field. Another. Coupled Harmonic Oscillators Hamiltonian.
From www.chegg.com
The Hamilton operator of a coupled twodimensional Coupled Harmonic Oscillators Hamiltonian A system of two coupled quantum harmonic oscillators with the hamiltonian h^ = 1 2(1 m1p^21 + 1 m2p^22 + ax21 + bx22 +. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. We will study in depth a particular system described by. Coupled Harmonic Oscillators Hamiltonian.
From www.researchgate.net
Synchronization of coupled harmonic oscillators Coupled Harmonic Oscillators Hamiltonian We will study in depth a particular system described by the h.o., the electromagnetic field. ˆp2 2 + ax2 1 + bx2 2 + cx1x2. Another system that can be described by this. In addition to presenting a physically important system, this lecture, reveals a very deep connection which. A system of two coupled quantum harmonic oscillators with the hamiltonian. Coupled Harmonic Oscillators Hamiltonian.