Coercive Operator . Coercive vector fields a vector field f : For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. 1.4 coercive functions and global min. A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the usual dot product and ‖ ‖ denotes the usual. Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. Then the alternative definition does not. Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol). To get an intuition, coercivity means that the vectors of the unit.
from jobanks.net
Coercive vector fields a vector field f : For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the usual dot product and ‖ ‖ denotes the usual. A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. To get an intuition, coercivity means that the vectors of the unit. Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol). 1.4 coercive functions and global min. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. Then the alternative definition does not. Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and.
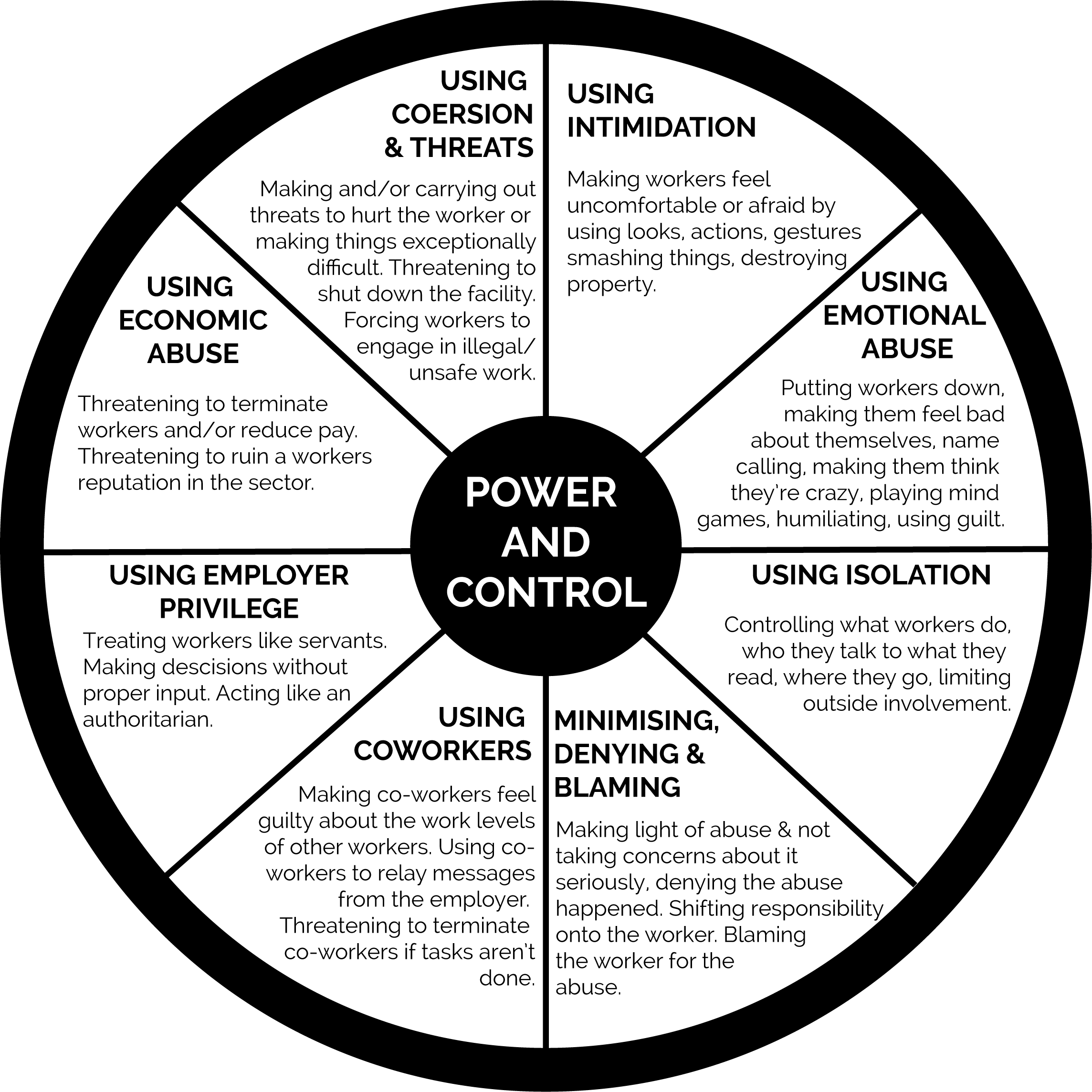
UNDERSTANDING COERCIVE CONTROL IN THE WORKPLACE Jo Banks
Coercive Operator Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol). Coercive vector fields a vector field f : A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the usual dot product and ‖ ‖ denotes the usual. 1.4 coercive functions and global min. Then the alternative definition does not. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. To get an intuition, coercivity means that the vectors of the unit. Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol). For coercivity there is often used the definition where ξ ξ is just a multiple of the identity.
From www.researchgate.net
Coercive and noncoercive clefs in translation Download Scientific Coercive Operator Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and. To get an intuition, coercivity means that the vectors of the unit.. Coercive Operator.
From www.ahmrc.org.au
Free coercive control training AH&MRC Coercive Operator 1.4 coercive functions and global min. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol). Coercive vector fields a vector. Coercive Operator.
From hannaylawyers.com.au
What You Need to Know About Coercive Hearings Hannay Lawyers Coercive Operator 1.4 coercive functions and global min. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the usual dot product and ‖ ‖ denotes the usual. A bounded operator. Coercive Operator.
From 16days.idas.org.uk
Coercive Control 16 Days 16 Stories Coercive Operator To get an intuition, coercivity means that the vectors of the unit. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. Then the alternative definition does not. A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. Coercive operator. Coercive Operator.
From www.researchgate.net
(PDF) An adaptive splitting algorithm for the sum of two generalized Coercive Operator For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. 1.4 coercive functions and global min. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. To get an intuition, coercivity means that. Coercive Operator.
From www.linkedin.com
What is Coercive Control? Coercive Operator Then the alternative definition does not. Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. A bounded operator doens't need to be coercive, for example l. Coercive Operator.
From helpfulprofessor.com
Coercive Organizations Definition and 10 Examples (Sociology) Coercive Operator Then the alternative definition does not. R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the usual dot product and ‖ ‖ denotes the usual. Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and. Here we prove carefully the main lemma concerning. Coercive Operator.
From nexusni.org
Coercive Control Blog Nexus NI Coercive Operator Then the alternative definition does not. Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol). For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. To get an intuition, coercivity means that the vectors of the unit. Here we prove carefully. Coercive Operator.
From www.researchgate.net
Solving monotone inclusions involving the sum of three maximally Coercive Operator Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. To get an intuition, coercivity means that the vectors of the unit. 1.4 coercive functions and global min. For coercivity there is often used the definition where ξ ξ is just a multiple of the identity.. Coercive Operator.
From www.researchgate.net
(PDF) H(·,·)Cocoercive Operator and an Application for Solving Coercive Operator A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. To get an intuition, coercivity means that the vectors of the unit. Then the alternative definition does not. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all. Coercive Operator.
From www.esaalliance.org
What is Coercive Control? — Enthusiastic Sobriety Abuse Alliance Coercive Operator 1.4 coercive functions and global min. For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. Coercive operator this is called as the. Coercive Operator.
From irepod.com
What Is Coercive Control? Recovery from Coercive Control Coercive Operator Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol). To get an intuition, coercivity means that the vectors of the unit. Coercive vector fields a vector field f : R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the usual dot. Coercive Operator.
From jobanks.net
UNDERSTANDING COERCIVE CONTROL IN THE WORKPLACE Jo Banks Coercive Operator A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol). Coercive vector fields a vector field f : Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator. Coercive Operator.
From www.researchgate.net
(PDF) GRAPH CONVERGENCE FOR H(.,.)COCOERCIVE OPERATOR IN qUNIFORMLY Coercive Operator 1.4 coercive functions and global min. Coercive vector fields a vector field f : R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the usual dot product and ‖ ‖ denotes the usual. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle. Coercive Operator.
From hopeforhurtingwives.com
What is Coercive Control? Hope for Hurting Wives Coercive Operator A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and. Let. Coercive Operator.
From valleyhouse.org.uk
coercive control Valley House Coercive Operator For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. Coercive vector fields a vector field f : Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. Theorem 1.11 (theorem 1.4.1) a continuous function f on a. Coercive Operator.
From www.safeguardingni.org
Coercive Control Animation Where is the line? Safeguarding Board Coercive Operator To get an intuition, coercivity means that the vectors of the unit. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. Then the alternative definition does not. For coercivity there is often used the definition where ξ ξ is just a multiple of the identity.. Coercive Operator.
From www.researchgate.net
Hypothetical model Coercive Download Scientific Diagram Coercive Operator Then the alternative definition does not. Coercive vector fields a vector field f : To get an intuition, coercivity means that the vectors of the unit. For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator. Coercive Operator.
From daykinfamilylaw.com.au
13 Signs of Coercive Control & How to Deal with Them Coercive Operator To get an intuition, coercivity means that the vectors of the unit. 1.4 coercive functions and global min. For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by.. Coercive Operator.
From www.learning-mind.com
20 Signs of Coercive Control That Reveal Manipulation in a Relationship Coercive Operator Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and. 1.4 coercive functions and global min. Let $v$ be a hilbert space and let $a:v \to v^*$. Coercive Operator.
From www.nidec.com
Coercive force, coercive intensity NIDEC CORPORATION Coercive Operator To get an intuition, coercivity means that the vectors of the unit. For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and. Here we prove carefully the main lemma concerning coercivity for operators. Coercive Operator.
From www.scribd.com
Chap2 Lec1 Coercive Functions and Global Minimizers PDF Eigenvalues Coercive Operator Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the usual dot product and ‖ ‖ denotes the usual. Coercive vector fields a vector field f : To. Coercive Operator.
From www.youtube.com
What is Coercive Control? YouTube Coercive Operator To get an intuition, coercivity means that the vectors of the unit. R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the usual dot product and ‖ ‖ denotes the usual. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the. Coercive Operator.
From www.betterup.com
Coercive power at work Examples, implications, and more Coercive Operator To get an intuition, coercivity means that the vectors of the unit. Coercive vector fields a vector field f : For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. 1.4 coercive functions and global min. Then the alternative definition does not. Theorem 1.11 (theorem 1.4.1) a continuous function f on a. Coercive Operator.
From www.itsmental.co.uk
What is Coercive Control? Mary Nicoll It's Mental Coercive Operator For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. Then the alternative definition does not. To get an intuition, coercivity means that the vectors of the unit. 1.4 coercive functions and global min. A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. R n. Coercive Operator.
From www.researchgate.net
(PDF) H(.,.,., .)ϕηcocoercive operator with an application to Coercive Operator Then the alternative definition does not. A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. To get an intuition, coercivity means that the vectors of the unit. 1.4 coercive functions and global min. Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol).. Coercive Operator.
From dokumen.tips
(PDF) What Is Coercive Control? DOKUMEN.TIPS Coercive Operator Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. Coercive operator this is called as the. Coercive Operator.
From www.betterup.com
Coercive power at work Examples, implications, and more Coercive Operator For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. 1.4 coercive functions and global min. Coercive operator this is called as the lax milgram theorem, but in. Coercive Operator.
From www.hallpayne.com.au
Coercive Control Laws in Queensland Hall Payne Lawyers Coercive Operator To get an intuition, coercivity means that the vectors of the unit. Coercive vector fields a vector field f : 1.4 coercive functions and global min. A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. R n → r n is called coercive if ‖ ‖ + ‖ ‖ +, where denotes the. Coercive Operator.
From yourtoolkit.com
What is Coercive Control? Coercive Operator Theorem 1.11 (theorem 1.4.1) a continuous function f on a closed bounded domain d has a global min and. Then the alternative definition does not. To get an intuition, coercivity means that the vectors of the unit. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played. Coercive Operator.
From divethru.com
Coercive Control What Is It and How Can You Spot It? DiveThru Coercive Operator For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. Coercive vector fields a vector field f : Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. A bounded operator doens't need to be coercive, for example. Coercive Operator.
From helpfulprofessor.com
25 Coercive Power Examples (2024) Coercive Operator A bounded operator doens't need to be coercive, for example l ≡ 0 l ≡ 0. Here we prove carefully the main lemma concerning coercivity for operators of the form l which are elliptic and explain the role played by. 1.4 coercive functions and global min. Coercive vector fields a vector field f : To get an intuition, coercivity means. Coercive Operator.
From yourtoolkit.com
Coercive Control Self‑Assessment Tool Coercive Operator For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. To get an intuition, coercivity means that the vectors of the unit. Coercive. Coercive Operator.
From adrtimes.com
Coercive Power How it Impacts Your Employees ADR Times Coercive Operator Coercive vector fields a vector field f : Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in v$. For coercivity there is often used the definition where ξ ξ is just a multiple of the identity. 1.4 coercive functions and global. Coercive Operator.
From signhealth.org.uk
Coercive Control Where is the line? SignHealth Coercive Operator To get an intuition, coercivity means that the vectors of the unit. Coercive operator this is called as the lax milgram theorem, but in lawrence and narici, it's a fucking lemma (lol). Let $v$ be a hilbert space and let $a:v \to v^*$ be a bounded linear operator such that $$\langle av, v \rangle \geq c|v|_v$$ for all $v \in. Coercive Operator.