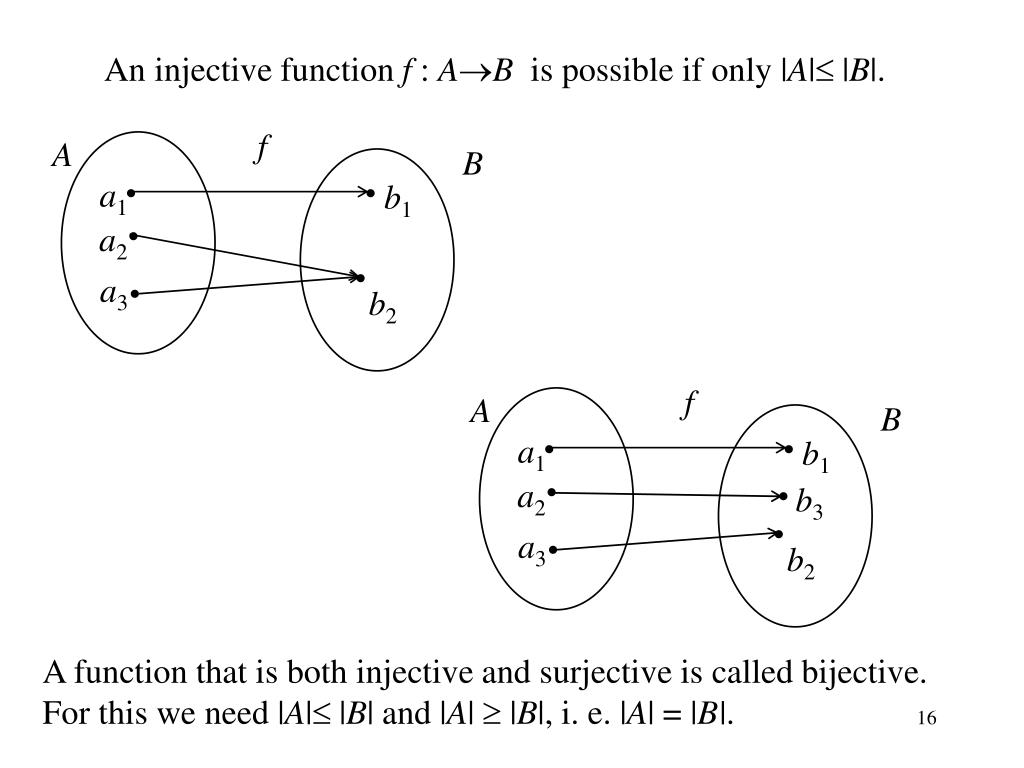
Correspondence Between Partitions And Equivalence Relations . Specifically, we define x ∼ y if and only if x and y are in the same. any partition p has a corresponding equivalence relation. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: For all \(x \in x\), \(x \sim x\). Every equivalence relation creates a partition, and every. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. there is a close correspondence between partitions and equivalence relations. math 4330 fall 2019 5 equivalence relations exercises eqrel 1.
from www.slideserve.com
if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. For all \(x \in x\), \(x \sim x\). any partition p has a corresponding equivalence relation. Every equivalence relation creates a partition, and every. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: there is a close correspondence between partitions and equivalence relations. Specifically, we define x ∼ y if and only if x and y are in the same.
PPT Equivalence relations and partitions . PowerPoint Presentation
Correspondence Between Partitions And Equivalence Relations an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: there is a close correspondence between partitions and equivalence relations. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. Specifically, we define x ∼ y if and only if x and y are in the same. Every equivalence relation creates a partition, and every. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: For all \(x \in x\), \(x \sim x\). any partition p has a corresponding equivalence relation.
From www.studocu.com
IUM 13 Equivalence relations, equivalence classes, and partitions 1 Correspondence Between Partitions And Equivalence Relations any partition p has a corresponding equivalence relation. there is a close correspondence between partitions and equivalence relations. Every equivalence relation creates a partition, and every. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Equivalence Relations. Partial Ordering Relations PowerPoint Correspondence Between Partitions And Equivalence Relations math 4330 fall 2019 5 equivalence relations exercises eqrel 1. For all \(x \in x\), \(x \sim x\). if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: Specifically, we define. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Equivalence relations and partitions . PowerPoint Presentation Correspondence Between Partitions And Equivalence Relations Specifically, we define x ∼ y if and only if x and y are in the same. there is a close correspondence between partitions and equivalence relations. any partition p has a corresponding equivalence relation. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. For all \(x \in x\), \(x \sim x\). if \(\sim\) is. Correspondence Between Partitions And Equivalence Relations.
From www.youtube.com
Equivalence Relations & Set Partitions, Part One YouTube Correspondence Between Partitions And Equivalence Relations if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. Every equivalence relation creates a partition, and every. For all \(x \in x\), \(x \sim x\). any partition p has a corresponding equivalence relation. an. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Binary Relation PowerPoint Presentation, free download ID6602392 Correspondence Between Partitions And Equivalence Relations if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. there is a close correspondence between partitions and equivalence relations. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. any partition p has a corresponding equivalence relation. Specifically, we define x ∼ y if. Correspondence Between Partitions And Equivalence Relations.
From www.studocu.com
AA1 Lesson 1 Abstract Algebra Lesson 1 Equivalence Relations and Correspondence Between Partitions And Equivalence Relations if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: there is a close correspondence between partitions and equivalence relations. math 4330 fall 2019 5 equivalence relations exercises eqrel 1.. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Minimal DFA PowerPoint Presentation, free download ID2629955 Correspondence Between Partitions And Equivalence Relations math 4330 fall 2019 5 equivalence relations exercises eqrel 1. For all \(x \in x\), \(x \sim x\). Every equivalence relation creates a partition, and every. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. Specifically, we define x ∼ y if and only if x. Correspondence Between Partitions And Equivalence Relations.
From www.youtube.com
Abstract Algebra Partitions and Equivalence Relations YouTube Correspondence Between Partitions And Equivalence Relations any partition p has a corresponding equivalence relation. For all \(x \in x\), \(x \sim x\). if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. Every equivalence relation creates a partition, and every. Specifically, we define x ∼ y if and only if x and y. Correspondence Between Partitions And Equivalence Relations.
From www.studocu.com
ERand Partitions Equivalence Relations and Partitions Theorem 3 Correspondence Between Partitions And Equivalence Relations For all \(x \in x\), \(x \sim x\). Specifically, we define x ∼ y if and only if x and y are in the same. any partition p has a corresponding equivalence relation. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. math 4330 fall. Correspondence Between Partitions And Equivalence Relations.
From www.showme.com
Equivalence relations and partitions ShowMe Correspondence Between Partitions And Equivalence Relations Specifically, we define x ∼ y if and only if x and y are in the same. any partition p has a corresponding equivalence relation. Every equivalence relation creates a partition, and every. For all \(x \in x\), \(x \sim x\). if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\). Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT EE1J2 Discrete Maths Lecture 8 PowerPoint Presentation, free Correspondence Between Partitions And Equivalence Relations Every equivalence relation creates a partition, and every. there is a close correspondence between partitions and equivalence relations. Specifically, we define x ∼ y if and only if x and y are in the same. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: any partition p has a corresponding equivalence. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Equivalence relations and partitions . PowerPoint Presentation Correspondence Between Partitions And Equivalence Relations any partition p has a corresponding equivalence relation. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. there is a close correspondence between partitions and equivalence relations. Specifically, we define x ∼ y if and only if x and y are in the same. . Correspondence Between Partitions And Equivalence Relations.
From teachoo.com
Example 41 If R1, R2 are equivalence relations in set A Correspondence Between Partitions And Equivalence Relations an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: there is a close correspondence between partitions and equivalence relations. Every equivalence relation creates a partition, and every. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. Specifically, we define. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Equivalence relations and partitions . PowerPoint Presentation Correspondence Between Partitions And Equivalence Relations For all \(x \in x\), \(x \sim x\). there is a close correspondence between partitions and equivalence relations. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. Every equivalence relation creates a partition, and every.. Correspondence Between Partitions And Equivalence Relations.
From slideplayer.com
Relations The Second Time Around ppt download Correspondence Between Partitions And Equivalence Relations For all \(x \in x\), \(x \sim x\). if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: Every equivalence relation creates a partition, and every. any partition p has a. Correspondence Between Partitions And Equivalence Relations.
From www.chegg.com
Solved Equivalence relations "are" partitions (continued). Correspondence Between Partitions And Equivalence Relations Specifically, we define x ∼ y if and only if x and y are in the same. For all \(x \in x\), \(x \sim x\). math 4330 fall 2019 5 equivalence relations exercises eqrel 1. Every equivalence relation creates a partition, and every. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is:. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Chapter 5 Relations and Functions PowerPoint Presentation, free Correspondence Between Partitions And Equivalence Relations any partition p has a corresponding equivalence relation. there is a close correspondence between partitions and equivalence relations. Specifically, we define x ∼ y if and only if x and y are in the same. Every equivalence relation creates a partition, and every. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that. Correspondence Between Partitions And Equivalence Relations.
From www.youtube.com
lec22 Equivalence Relations and Partitions YouTube Correspondence Between Partitions And Equivalence Relations any partition p has a corresponding equivalence relation. Every equivalence relation creates a partition, and every. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. For all \(x \in x\), \(x \sim x\). an equivalence relation on a set \(x\) is a relation \(\sim\) on. Correspondence Between Partitions And Equivalence Relations.
From www.youtube.com
Important Math Proof The Set of Equivalence Classes Partition a Set Correspondence Between Partitions And Equivalence Relations For all \(x \in x\), \(x \sim x\). math 4330 fall 2019 5 equivalence relations exercises eqrel 1. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: any partition p has a corresponding equivalence relation. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Equivalence relations and partitions . PowerPoint Presentation Correspondence Between Partitions And Equivalence Relations any partition p has a corresponding equivalence relation. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. For all \(x \in x\), \(x \sim x\). if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. Every equivalence relation creates a partition, and every. Specifically, we. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Discrete Mathematics Equivalence Relations PowerPoint Correspondence Between Partitions And Equivalence Relations there is a close correspondence between partitions and equivalence relations. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. any partition p has a corresponding equivalence relation. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: For all \(x \in x\), \(x \sim x\). Every equivalence relation creates a. Correspondence Between Partitions And Equivalence Relations.
From slideplayer.com
Equivalence Relations ppt download Correspondence Between Partitions And Equivalence Relations if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. Specifically, we define x ∼ y if and only if x and y are in the same. For all \(x \in x\), \(x \sim x\). an equivalence relation on a set \(x\) is a relation \(\sim\) on. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Equivalence relations and partitions . PowerPoint Presentation Correspondence Between Partitions And Equivalence Relations an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: any partition p has a corresponding equivalence relation. For all \(x \in x\), \(x \sim x\). Every equivalence relation creates a partition, and every. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. Specifically, we define x ∼ y if and. Correspondence Between Partitions And Equivalence Relations.
From www.chegg.com
Solved 12. A Partition Defines an Equivalence Relation. Let Correspondence Between Partitions And Equivalence Relations For all \(x \in x\), \(x \sim x\). an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: Every equivalence relation creates a partition, and every. there is a close correspondence between partitions and equivalence relations. any partition p has a corresponding equivalence relation. if \(\sim\) is an equivalence relation on. Correspondence Between Partitions And Equivalence Relations.
From calcworkshop.com
Equivalence Relation (Defined w/ 17 StepbyStep Examples!) Correspondence Between Partitions And Equivalence Relations an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: For all \(x \in x\), \(x \sim x\). math 4330 fall 2019 5 equivalence relations exercises eqrel 1. any partition p has a corresponding equivalence relation. Specifically, we define x ∼ y if and only if x and y are in the. Correspondence Between Partitions And Equivalence Relations.
From calcworkshop.com
Equivalence Relation (Defined w/ 17 StepbyStep Examples!) Correspondence Between Partitions And Equivalence Relations there is a close correspondence between partitions and equivalence relations. For all \(x \in x\), \(x \sim x\). Every equivalence relation creates a partition, and every. any partition p has a corresponding equivalence relation. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: Specifically, we define x ∼ y if and. Correspondence Between Partitions And Equivalence Relations.
From exoqytoqy.blob.core.windows.net
Equivalence Class Partitioning Examples at Sherryl Maxwell blog Correspondence Between Partitions And Equivalence Relations math 4330 fall 2019 5 equivalence relations exercises eqrel 1. For all \(x \in x\), \(x \sim x\). Specifically, we define x ∼ y if and only if x and y are in the same. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: if \(\sim\) is an equivalence relation on. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Equivalence relations and partitions . PowerPoint Presentation Correspondence Between Partitions And Equivalence Relations if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. Every equivalence relation creates a partition, and every. there is a close correspondence between partitions and equivalence relations. For all \(x \in x\), \(x \sim x\). math 4330 fall 2019 5 equivalence relations exercises eqrel 1.. Correspondence Between Partitions And Equivalence Relations.
From www.youtube.com
Equivalence Classes and Partitions YouTube Correspondence Between Partitions And Equivalence Relations an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is: Specifically, we define x ∼ y if and only if x and y are in the same. For all \(x \in x\), \(x \sim x\). Every equivalence relation creates a partition, and every. math 4330 fall 2019 5 equivalence relations exercises eqrel 1.. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Alan Mishchenko PowerPoint Presentation, free download ID6622706 Correspondence Between Partitions And Equivalence Relations For all \(x \in x\), \(x \sim x\). Specifically, we define x ∼ y if and only if x and y are in the same. Every equivalence relation creates a partition, and every. there is a close correspondence between partitions and equivalence relations. an equivalence relation on a set \(x\) is a relation \(\sim\) on \(x\) that is:. Correspondence Between Partitions And Equivalence Relations.
From math.stackexchange.com
real analysis On 11 correspondence and equivalence relation Correspondence Between Partitions And Equivalence Relations any partition p has a corresponding equivalence relation. there is a close correspondence between partitions and equivalence relations. Specifically, we define x ∼ y if and only if x and y are in the same. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. . Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Equivalence relations and partitions . PowerPoint Presentation Correspondence Between Partitions And Equivalence Relations there is a close correspondence between partitions and equivalence relations. Every equivalence relation creates a partition, and every. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. For all \(x \in x\), \(x \sim x\). any partition p has a corresponding equivalence relation. math. Correspondence Between Partitions And Equivalence Relations.
From www.chegg.com
Solved Equivalence relations "are" partitions. Let S be a Correspondence Between Partitions And Equivalence Relations if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. Every equivalence relation creates a partition, and every. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. Specifically, we define x ∼ y if and only if x and y are in the same. For all. Correspondence Between Partitions And Equivalence Relations.
From www.slideserve.com
PPT Equivalence relations and partitions . PowerPoint Presentation Correspondence Between Partitions And Equivalence Relations any partition p has a corresponding equivalence relation. Specifically, we define x ∼ y if and only if x and y are in the same. math 4330 fall 2019 5 equivalence relations exercises eqrel 1. For all \(x \in x\), \(x \sim x\). if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence. Correspondence Between Partitions And Equivalence Relations.
From cshub.in
Equivalence Relations and Partitions Discrete Mathematical Structures Correspondence Between Partitions And Equivalence Relations math 4330 fall 2019 5 equivalence relations exercises eqrel 1. if \(\sim\) is an equivalence relation on \(s\text{,}\) then the set of all equivalence classes of \(s\) under \(\sim\) is a. For all \(x \in x\), \(x \sim x\). Every equivalence relation creates a partition, and every. Specifically, we define x ∼ y if and only if x. Correspondence Between Partitions And Equivalence Relations.