Damping Effect On Natural Frequency at Carl Ward blog

Damping Effect On Natural Frequency. a system’s natural frequency is the frequency at which the system will oscillate if not affected by driving or damping forces. how does damping affect natural frequency? i am curious about that since damping will not affect frequency of shm, then why it does affect on the natural frequency of the shm. given that the amplitude is a proxy for the energy in the system, this means that more energy is added to the system by a driving force. for a system that has a small amount of damping, the period and frequency are constant and are nearly the same as for shm, but the amplitude gradually. In the absence of a damping term, the ratio k=mwould be the square of the angular. furthermore, for excitation at the natural frequency, \(\omega=\omega_{n}\), response lags excitation by exactly 90°, regardless of the level of viscous. A periodic force driving a. it is illustrated in the mathlet damping ratio.

A periodic force driving a. furthermore, for excitation at the natural frequency, \(\omega=\omega_{n}\), response lags excitation by exactly 90°, regardless of the level of viscous. a system’s natural frequency is the frequency at which the system will oscillate if not affected by driving or damping forces. how does damping affect natural frequency? given that the amplitude is a proxy for the energy in the system, this means that more energy is added to the system by a driving force. it is illustrated in the mathlet damping ratio. for a system that has a small amount of damping, the period and frequency are constant and are nearly the same as for shm, but the amplitude gradually. i am curious about that since damping will not affect frequency of shm, then why it does affect on the natural frequency of the shm. In the absence of a damping term, the ratio k=mwould be the square of the angular.

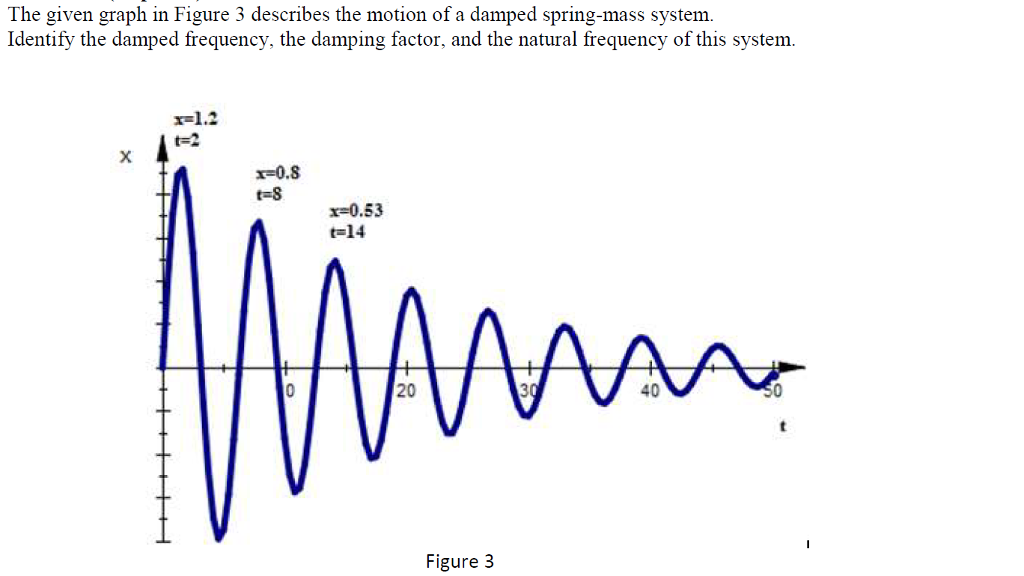
Solved The given graph in Figure 3 describes the motion of a

Damping Effect On Natural Frequency In the absence of a damping term, the ratio k=mwould be the square of the angular. a system’s natural frequency is the frequency at which the system will oscillate if not affected by driving or damping forces. In the absence of a damping term, the ratio k=mwould be the square of the angular. furthermore, for excitation at the natural frequency, \(\omega=\omega_{n}\), response lags excitation by exactly 90°, regardless of the level of viscous. for a system that has a small amount of damping, the period and frequency are constant and are nearly the same as for shm, but the amplitude gradually. given that the amplitude is a proxy for the energy in the system, this means that more energy is added to the system by a driving force. i am curious about that since damping will not affect frequency of shm, then why it does affect on the natural frequency of the shm. A periodic force driving a. it is illustrated in the mathlet damping ratio. how does damping affect natural frequency?