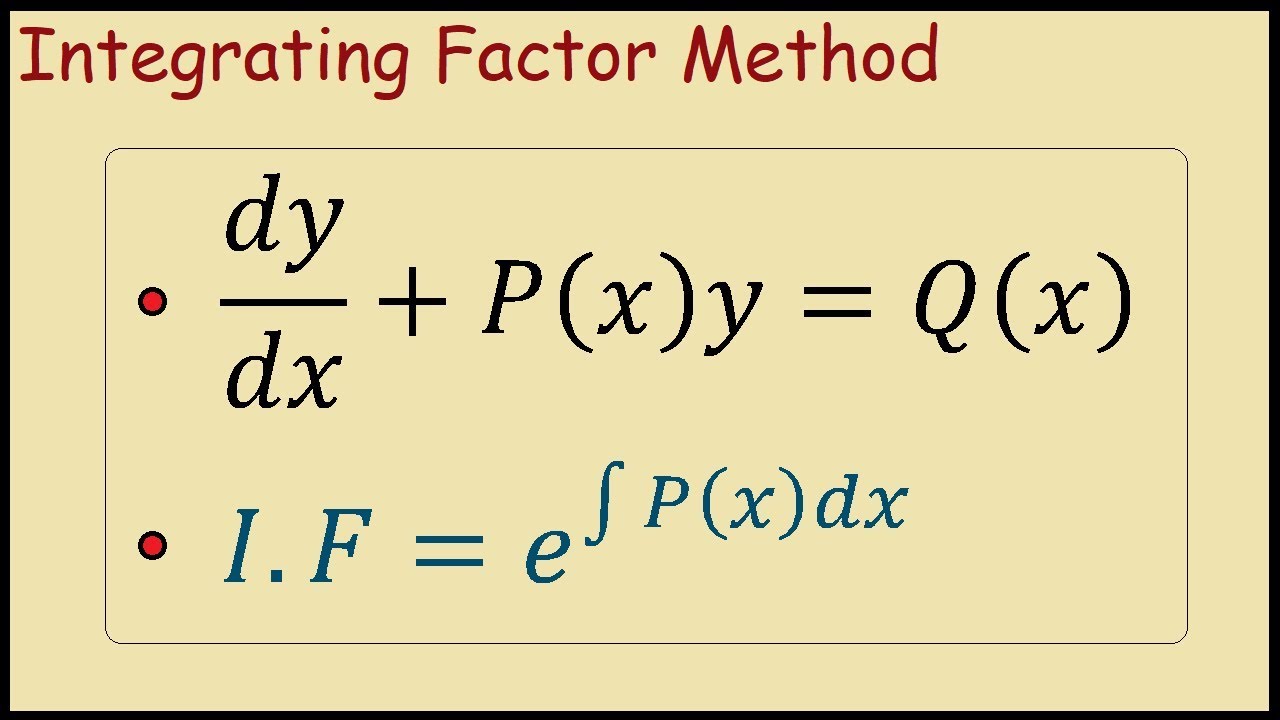Differential Equations Integrating Factor . a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. We are looking for a. Find the definition, steps, examples and. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. start practicing—and saving your progress—now: We give an in depth overview. illustration of the procedure to find an integrating factor that allows integration of a first order linear ordinary differential. Differential equations in the form y' + p(t) y = g(t). If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. in this section we solve linear first order differential equations, i.e.
from
a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. We are looking for a. in this section we solve linear first order differential equations, i.e. If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. We give an in depth overview. start practicing—and saving your progress—now: Find the definition, steps, examples and. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. Differential equations in the form y' + p(t) y = g(t).
Differential Equations Integrating Factor We give an in depth overview. start practicing—and saving your progress—now: Differential equations in the form y' + p(t) y = g(t). Find the definition, steps, examples and. We are looking for a. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. in this section we solve linear first order differential equations, i.e. a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. illustration of the procedure to find an integrating factor that allows integration of a first order linear ordinary differential. If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. We give an in depth overview. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.
From
Differential Equations Integrating Factor start practicing—and saving your progress—now: illustration of the procedure to find an integrating factor that allows integration of a first order linear ordinary differential. If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. Differential equations in the form y' + p(t) y =. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor start practicing—and saving your progress—now: Find the definition, steps, examples and. If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. illustration of the procedure to find an integrating factor that allows integration of a first order linear ordinary differential. the function \(r(x)\). Differential Equations Integrating Factor.
From www.teachoo.com
Ex 9.6, 18 The integrating factor of differential equation Differential Equations Integrating Factor We are looking for a. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. start practicing—and saving your progress—now: Differential equations in the form y' + p(t) y = g(t). Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact.. Differential Equations Integrating Factor.
From www.youtube.com
Nonexact differential equation with integrating factor example YouTube Differential Equations Integrating Factor We give an in depth overview. Differential equations in the form y' + p(t) y = g(t). the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. Find the definition, steps, examples and. start practicing—and saving your progress—now: illustration of the procedure to find an integrating factor that allows integration. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. Differential equations in the form y' + p(t) y = g(t). Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. We give an in depth. Differential Equations Integrating Factor.
From www.youtube.com
Exact Differential Equations Using an Integrating Factor YouTube Differential Equations Integrating Factor Find the definition, steps, examples and. illustration of the procedure to find an integrating factor that allows integration of a first order linear ordinary differential. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor We give an in depth overview. We are looking for a. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Find the definition, steps, examples and. illustration of the procedure to find an integrating factor that allows integration of a first order linear ordinary differential. If we know. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor We are looking for a. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. start practicing—and saving your progress—now: in this section we solve linear first order differential. Differential Equations Integrating Factor.
From www.youtube.com
Introduction to Linear Differential Equations and Integrating Factor AP Calculus 12 YouTube Differential Equations Integrating Factor Find the definition, steps, examples and. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. Differential equations in the form y' + p(t) y = g(t). illustration of the procedure. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. We are looking for a. in this section we solve linear first order differential equations, i.e. We give an in depth overview. If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4}. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. in this section we solve linear first order differential equations, i.e. We are looking for a. If we know an integrating factor. Differential Equations Integrating Factor.
From www.youtube.com
First Order Linear Differential Equations Integrating Factors Examples Level 1 YouTube Differential Equations Integrating Factor a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. We are looking for a. Find the definition, steps, examples and. in this section we solve linear first order differential equations, i.e.. Differential Equations Integrating Factor.
From www.youtube.com
Differential Equations Integrating factor type (Examples) ExamSolutions Maths Tutorials YouTube Differential Equations Integrating Factor Differential equations in the form y' + p(t) y = g(t). We give an in depth overview. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. start practicing—and saving your. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor start practicing—and saving your progress—now: If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. Differential equations in the form y' + p(t) y = g(t). Find the definition, steps, examples and. We give an in depth overview. illustration of the procedure to find. Differential Equations Integrating Factor.
From www.slideserve.com
PPT Differential Equations PowerPoint Presentation, free download ID3965971 Differential Equations Integrating Factor start practicing—and saving your progress—now: the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. Find the definition, steps, examples and. We are looking for a. a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. Some equations that are not exact. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. We are looking for a. a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. We give an in depth overview. illustration of the procedure to. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. Find the definition, steps, examples and. We give an in depth overview. Some equations that are not exact may be multiplied by some. Differential Equations Integrating Factor.
From www.youtube.com
solve differential equation using integrating factor part 3 YouTube Differential Equations Integrating Factor If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. We are looking for a. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. We give an in depth overview. a function \(\mu=\mu(x,y)\) is an integrating. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor We are looking for a. We give an in depth overview. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. in this section we solve linear first order differential equations, i.e. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor. Differential Equations Integrating Factor.
From www.slideserve.com
PPT Differential Equations PowerPoint Presentation, free download ID1806377 Differential Equations Integrating Factor Differential equations in the form y' + p(t) y = g(t). If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. Find the definition, steps, examples and. We are looking for a. start practicing—and saving your progress—now: Some equations that are not exact may be. Differential Equations Integrating Factor.
From www.youtube.com
Integrating Factor Differential Equations YouTube Differential Equations Integrating Factor a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. We give an in depth overview. start practicing—and saving your progress—now: Find the definition, steps, examples and. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. Differential equations in the form. Differential Equations Integrating Factor.
From www.youtube.com
24 1 Solving First order differential equations using Integrating Factor A level Further Maths Differential Equations Integrating Factor We give an in depth overview. If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. in this section we solve linear first order differential equations, i.e. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method.. Differential Equations Integrating Factor.
From www.youtube.com
Solving a first order linear differential equation with the integrating factor method YouTube Differential Equations Integrating Factor in this section we solve linear first order differential equations, i.e. If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Find the definition, steps,. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor We give an in depth overview. in this section we solve linear first order differential equations, i.e. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. Find the definition, steps,. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor Differential equations in the form y' + p(t) y = g(t). start practicing—and saving your progress—now: We are looking for a. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. in this section we solve linear first order differential equations, i.e. Some equations that are not exact may be. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. Find the definition, steps, examples and. a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. in this section we solve linear first order differential equations, i.e. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Find the definition, steps,. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor Find the definition, steps, examples and. We give an in depth overview. in this section we solve linear first order differential equations, i.e. Differential equations in the form y' + p(t) y = g(t). the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. We are looking for a. illustration. Differential Equations Integrating Factor.
From www.youtube.com
Integrating Factor Method Differential Equations YouTube Differential Equations Integrating Factor start practicing—and saving your progress—now: We are looking for a. If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. We give an in depth overview. . Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor We are looking for a. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. illustration of the procedure to find an integrating factor that allows integration of a first order linear ordinary differential. Differential equations in the form y' + p(t) y = g(t). Find the definition, steps, examples and.. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation \ref{eq:2.6.4} by the method of section 2.5. a function \(\mu=\mu(x,y)\) is an integrating factor for equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)m (x,y)\,dx+\mu(x,y)n (x,y)\,dy=0 \] is exact. start practicing—and saving your progress—now: Find the definition, steps, examples and. Differential equations in the form. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor We are looking for a. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. If we know an integrating factor \(\mu\) for equation \ref{eq:2.6.1}, we can solve the exact equation equation. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor start practicing—and saving your progress—now: We are looking for a. We give an in depth overview. in this section we solve linear first order differential equations, i.e. Find the definition, steps, examples and. the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. If we know an integrating factor \(\mu\). Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor the function \(r(x)\) is called the integrating factor and the method is called the integrating factor method. start practicing—and saving your progress—now: Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. illustration of the procedure to find an integrating factor that allows integration of a first. Differential Equations Integrating Factor.
From
Differential Equations Integrating Factor We give an in depth overview. Some equations that are not exact may be multiplied by some factor, a function u(x, y), to make them exact. Differential equations in the form y' + p(t) y = g(t). in this section we solve linear first order differential equations, i.e. Find the definition, steps, examples and. start practicing—and saving your. Differential Equations Integrating Factor.