Square Root With Compass And Straightedge at Todd Crutcher blog

Square Root With Compass And Straightedge. I think i found a different way than usually shown which looks like this. For a given circle, construct a square of the same area. Find the midpoint of ba, and make a circle whose diameter is ba. With your straightedge and compass, you are allowed to: By several arguments given in. The ability to construct a straight line in any direction from any starting point with the unit length, or the length whose square root of its magnitude yields its own magnitude. Using a straight edge and compass only, they were: Draw the line l(p, q) (with the straightedge) through any two points p and q that you have already constructed. Construct a perpendicular to ba at d. Given the unit length , and the segment of length construct. How to do the construction with straightedge and compass or geometry software: It intersects the circle at c. The square root of two is constructible as the hypotenuse of a square who side length is 1. On a ray, mark off a distance 1 (bd), then a further distance da=n. The proof depends on several other ingredients.

The ability to construct a straight line in any direction from any starting point with the unit length, or the length whose square root of its magnitude yields its own magnitude. It intersects the circle at c. Square root using straightedge and compass. For a given circle, construct a square of the same area. Draw the line l(p, q) (with the straightedge) through any two points p and q that you have already constructed. By several arguments given in. Square and square root construction by compass and straightedge. With your straightedge and compass, you are allowed to: I think i found a different way than usually shown which looks like this. Using a straight edge and compass only, they were:

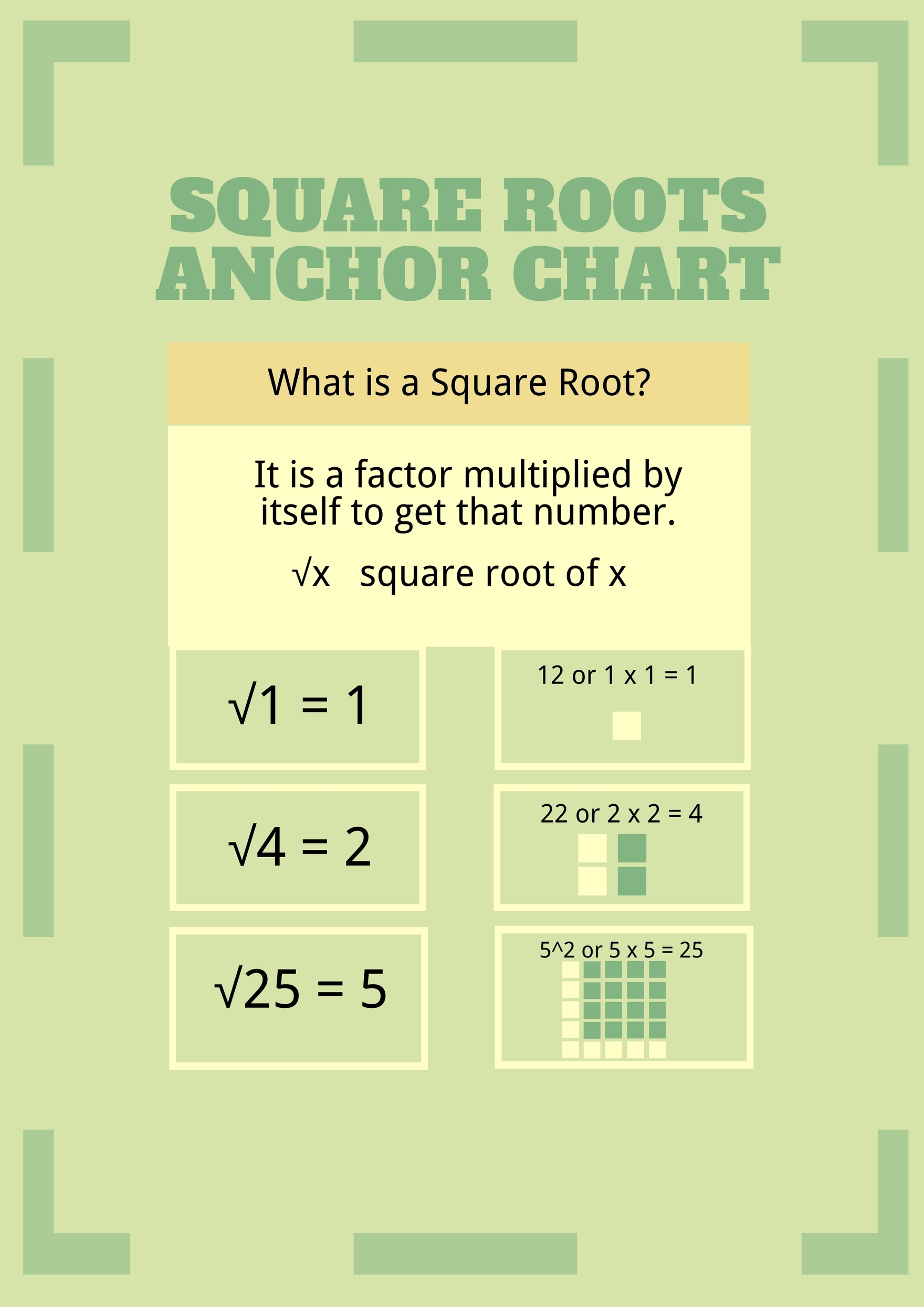
Square Root Anchor Chart

Square Root With Compass And Straightedge The square root of two is constructible as the hypotenuse of a square who side length is 1. Given the unit length , and the segment of length construct. The proof depends on several other ingredients. With your straightedge and compass, you are allowed to: How to do the construction with straightedge and compass or geometry software: Using a straight edge and compass only, they were: Draw the line l(p, q) (with the straightedge) through any two points p and q that you have already constructed. Let be the right angle triangle with and. I think i found a different way than usually shown which looks like this. For a given circle, construct a square of the same area. The ability to construct a straight line in any direction from any starting point with the unit length, or the length whose square root of its magnitude yields its own magnitude. Square and square root construction by compass and straightedge. Construct a perpendicular to ba at d. It intersects the circle at c. By several arguments given in. On a ray, mark off a distance 1 (bd), then a further distance da=n.